---------注:本文所用的术语定义均来自国外大学和计算机文献使用的定义,非国内教材。层次编号从1开始-------------
树的定义
树(generic tree):树是含有n个结点的有限集,结点(node)通过边(edge)连接起来,形成树状的非线性结构。
当 n=0时,为空树。
当 n>0时,仅有一个特殊的结点叫做根(root)的结点,它位于树的逻辑形态的最顶层,它没有父结点。
树都可以看做是 连通 无环 图,即树中的结点都是连通的,且不构成环。
树中的边(edge)是隐式有向的,方向从父结点指向他的每一个孩子结点。parent->children。
树中的结点,除了根结点外,每一个结点都有一个父结点,以及0个或者多个孩子结点。
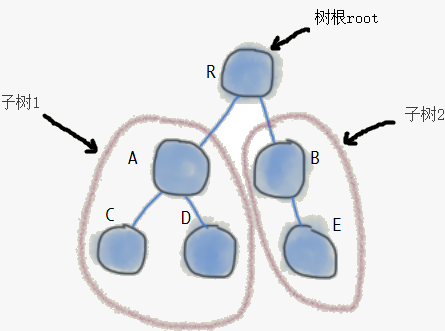
树的逻辑结构类似一颗倒立着的真实世界里的树。如下图中,整体是一个有6个结点的树。R为树根,其余结点又可以找出2棵子树:子树1 , 子树2。子树1中,结点A又是子树1的root结点,而结点C 和 结点D又是 子树1 的2个子树。
基本概念和名词解释
结点(node) : 树中存储 数据元素以及 结点之间的逻辑连接信息的数据。图中使用一个圆圈表示。
边(edge):结点与结点之间的逻辑连接,是2个结点构成的二元组。图中用一条线表示。
路径(path): 一个结点和他的某一个子孙之间的通路,是由结点构成的序列。如(A , B ,E)就是A到E的路径。路径长就是这个序列代表的边数目。
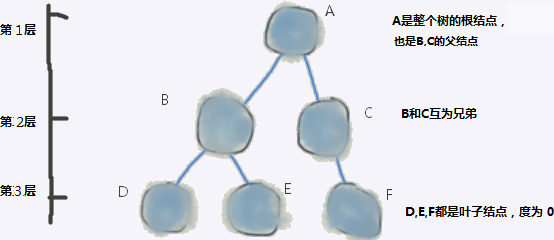
根结点(root):位于树的逻辑结构的最顶层的结点。下图的结点A即是。
叶子结点(leaf):没有任何孩子结点的结点(度为0)。下图中的D,E,F都是叶子结点。叶子结点又叫外部结点(external)。
内部结点(internal):非叶子结点即为内部结点。
结点的度(degree):结点的子树的个数,即结点的孩子数。
结点的深度(depth):从root结点到该结点的边的条数。(在具体实现时,可以求这个结点的祖先的个数作为他的深度,root 的深度是0)
结点的高度(height):从该节点到它能到达的所有叶子的路径中最长的路径长度。(叶子结点的高是0)结点的层次(level) :结点到root结点之间的边数 +1 ,即结点的深度+1
树的深度(tree depth):最深的叶子结点的深度。(树的深度和他的高度总是相等的)
树的高度(tree height):root结点的高度。(树的深度和他的高度总是相等的)
树的层次(tree level):以root结点为第1层,root的孩子为第2层,以此类推。
父结点(parent):下图中,A是 B和C共同的父节点。除了root结点外,一个结点仅有一个父结点。root结点无父结点。
孩子结点(child):一个结点的 直接子结点,叫做这个结点的孩子结点。下图中,A的孩子为B,C。
兄弟结点(sibling):拥有同一个parent的结点之间称为兄弟。
祖先(ancestor):一般指真祖先,即不包括结点本身。一个结点的父结点,父结点的父结点...一直向上到root结点,都是他的祖先。下图,E的祖先是B和A。
子孙(descendant):一般指真子孙,即不包括结点本身。以某结点为root结点的所有结点都是这个结点的子孙。下图B的子孙是D,E。
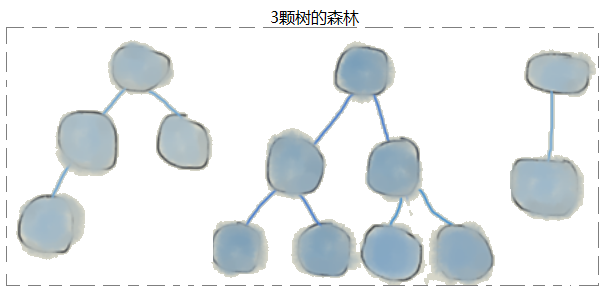
森林
定义:0个或者多个不相交的树形成森林。
无回路且不一定连通的 图叫做森林,其中每一个连通分量为一个树。
树的性质
如果树非空,则 结点数 总比 边数 多 1: N = E + 1
证明:除了root结点外,其余的结点都由 一条边引出来的(具体到图中,每个圆圈头上都有“一根草”),而root结点则没有,这就是少一的原因。
树的分类
一般树(generic tree):树中每个结点的孩子数目是不确定的,0个或多个。二叉树是generic tree的特例。
自由树(free tree):即无环连通图,这种树我们倾向于用图的眼光去看待它,因为他没有指定那一个结点是root,他的任何结点都可以是root。
有根树(rooted tree):明确指定了root结点的树,树的形态非常明显。一般我们谈论的树就是指有根树。
按照子结点是否有序分:
有序树:树中的每一个结点的所有孩子结点在逻辑上都是在意顺序的,是有序的:第一个孩子,第二个孩子,第三个孩子...第n个孩子。
无序数:树中的每一个结点的孩子结点不在意他们的放置顺序,是无序的。
按照形态分 :
树 --
二叉树--
满二叉树
完全二叉树
完美二叉树
...
三叉树
四叉树
五叉树
...
树和图的关系
树都可以看做是 连通(没有孤岛), 无环 (从一个结点出发只有唯一的一条路径到达另一个结点),无向图,如果特别说明,也可以是有向图。如果将一个树看做是无向图,则可以任取一个结点为root,将得到不同意义的树。
一般树的存储实现
一般树(generic tree),特点是每个结点的度是不确定的。
这里介绍2种存储实现。
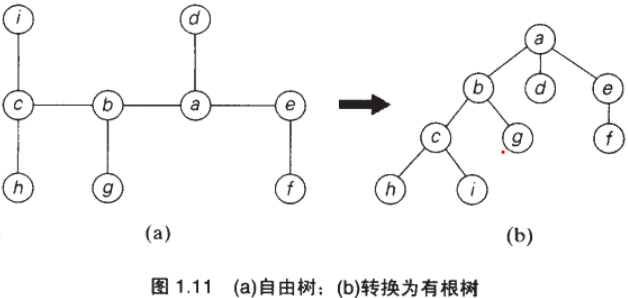
1、左孩子右兄弟表示法:将一般树转化为二叉树来存储,在一个一般树GT对应的二叉树BT中,每一个结点的左孩子对应GT中的这个结点的第一个孩子,而每一个结点的右孩子对应GT中这个结点的下一个相邻的兄弟。
摘自维基百科:如下左边是一个一般树,右边是它对应的二叉树。
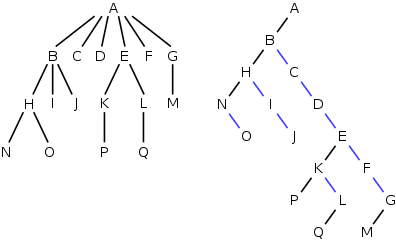
class GenericTreeNode<T> { private T element; private GenericTreeNode<T> nextSibling; //下一个兄弟 private GenericTreeNode<T> firstChild; //第一个孩子 //... }
2、孩子链表表示法
结点的域有3个:element保存数据,parent保存这个结点的父结点的引用,children是一个保存他的所有孩子的引用的线性表。
如果不需要访问父结点,则可以去掉parent域。

class GenericTreeNode<T> { private T element; private GenericTreeNode<T> parent; //父结点的引用 private List<GenericTreeNode<T>> children; //保存所有孩子结点的引用的线性表 //... }