中国剩余定理
问题
求解同余方程组
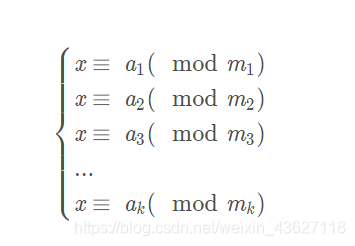
其中为两两互质的整数
求x的最小非负整数解
定理
令,即M是所有 的最小公倍数
为同余方程 的最小非负整数解
则有一个解为
通解为
特别的,最小非负整数解为(x%M+M)%M
证明

代码实现
同余式的求解可以用扩展欧几里得
void exgcd(int a,int b,int &x,int &y)
{
if(b==0){ x=1; y=0; return;}
exgcd(b,a%b,x,y);
int tp=x;
x=y; y=tp-a/b*y;
}
int china()
{
int ans=0,lcm=1,x,y;
for(int i=1;i<=k;++i) lcm*=b[i];
for(int i=1;i<=k;++i)
{
int tp=lcm/b[i];
exgcd(tp,b[i],x,y);
x=(x%b[i]+b[i])%b[i];//x要为最小非负整数解
ans=(ans+tp*x*a[i])%lcm;
}
return (ans+lcm)%lcm;
}
扩展中国剩余定理
求解同余方程组
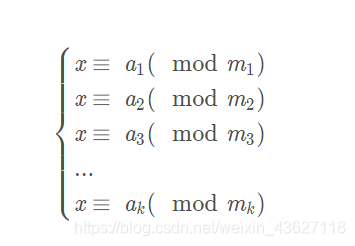
其中不一定为两两互质的整数
求x的最小非负整数解
求解:
求解
假设已经求出前k-1个方程组成的同余方程组的一个解为x
且有
则前k-1个方程的方程组通解为x+i∗M(i∈Z)x+i*M(iin Z)x+i∗M(i∈Z)
那么对于加入第k个方程后的方程组
我们就是要求一个正整数t,使得
转化一下上述式子得
对于这个式子我们已经可以通过扩展欧几里得求解t
若该同余式无解,则整个方程组无解
若有,则前k个同余式组成的方程组的一个解解为
所以整个算法的思路就是求解k次扩展欧几里得
#include<iostream>
using namespace std;
#define LL long long
LL mi[1100],ai[1100];//mi为要模的数,ai为余数。
LL gcd(LL a, LL b)
{
return b == 0 ? a : gcd(b, a%b);
}
void exgcd(LL a, LL b, LL &d, LL &x, LL &y)
{
if(!b)
{
d = a, x = 1, y = 0;
}
else
{
exgcd(b, a%b, d, y, x);
y -= x * (a / b);
}
}
LL CRT(LL l, LL r, LL *mi, LL *ai)
{
LL lcm = 1;
for(LL i = l; i <= r; i++)
lcm = lcm / gcd(lcm, mi[i]) * mi[i];
for(LL i = l+1; i <= r; i++)
{
LL A = mi[l], B = mi[i], d, x, y, c = ai[i] - ai[l];
exgcd(A, B, d, x, y);
if(c % d)
return -1;
LL mod = mi[i] / d;
LL k = ((x * c / d) % mod + mod) % mod;
ai[l] = mi[l] * k + ai[l];
mi[l] = mi[l] * mi[i] / d;
}
/*if(ai[l] == 0)
return lcm;*/ //保证结果为正整数
return ai[l];
}
int main()
{
LL t,n,i,aa;
while(cin>>n>>aa)
{
if(n==0) break;
for(i=1; i<=n; i++){
cin>>mi[i];
ai[i]=mi[i]-aa;
}
cout<<CRT(1ll,n,mi,ai)<<endl;
}
return 0;
}