SVC之SMO算法理解

SMO算法论文链接：https://www.microsoft.com/en-us/research/publication/sequential-minimal-optimization-a-fast-algorithm-for-training-support-vector-machines/

在SVC中，假设划分超平面f(x)为：

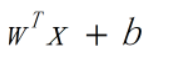
 我们的目标为找到一个这样的超平面f(x)：对于正例y=1，有w^tx+b>=1；对于反例y=-1，有w^tx+b<=-1。并使得间隔最大化。

其中，w^tx+b=1或-1的样本为支持向量。

间隔定义为：

 

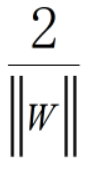
 目标为最大化间隔，即最小化：min_w,b ||w||²/2。条件为y_i(w^tx_i+b)>=1.

使用拉格朗日乘数法，转为为对偶问题：

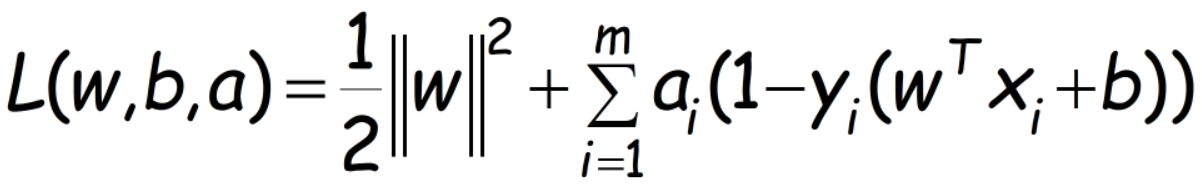
对w和b求导并设为0，得到：

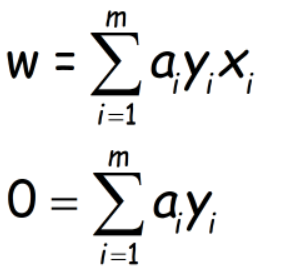
 代入L中，得到目标为：

                 

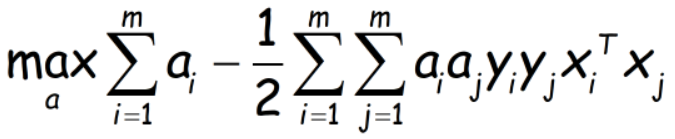
也即

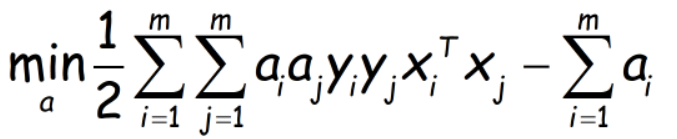                 ...................（1）

约束条件为a_i>=0及

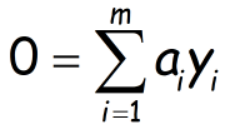
 KKT条件为：

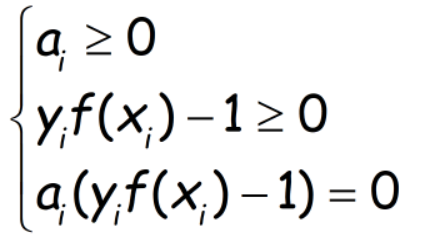
注意到a_i和y_i(f(x_i)-1)必有一个为0，当a_i不为0时，才对L有影响，此时另一个为0，起作用的都是间隔边界处的支持向量，即解为稀疏性的

下面进入到SMO算法细节，即如何更新这些a_i

其思路是：由于存在以下约束，每次选择2个变量a_i和a_j，固定其他变量，这样可以用a_i表示a_j，代入前面的（1）式子中求出a_i,再求出a_j

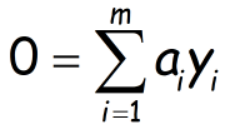                                      ...........（2）

 当使用“软间隔”时，优化目标为：

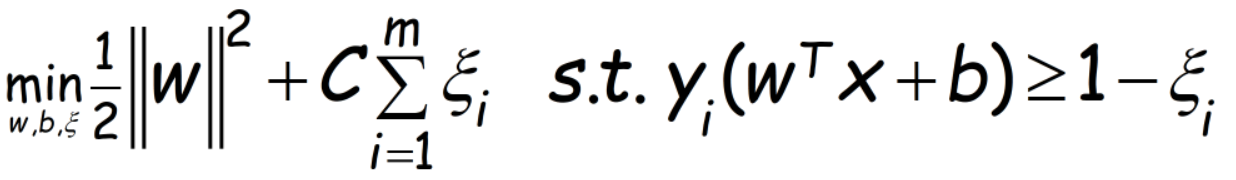
 其中ξ为松弛变量，典型值取为0.001，表示样本偏离间隔多少依然算做正或反例，C为偏离造成损失的权重（线性0.05，RBF取1），C越大，样本处于间隔内造成的损失越大，无穷大时退回到原始“硬间隔”问题。

 转化为对偶问题，（1）式优化形式不变，约束从ai>=0变为0<=ai<=C。KKT条件（以下通过原始KKT条件和约束推导而来）可以描述为：

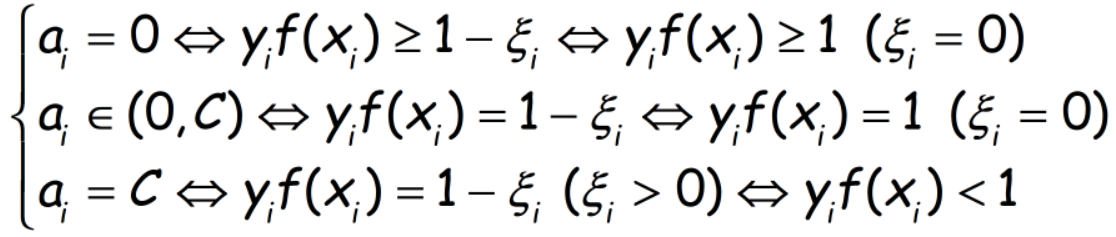
可以看到， 我们在考虑一个样本是否违反KKT条件时，只有当ai=C时，才需要用到松弛变量。

当我们选定了需要更新的2个ai和aj，因为约束(2)存在，则有：

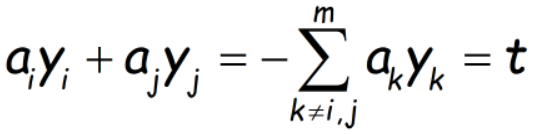                 ....................(3)

 因为y只取1和-1，则上式只有以下2种情况：即首先约束范围在一个矩形区域内，然后由上式约束在一条直线上。

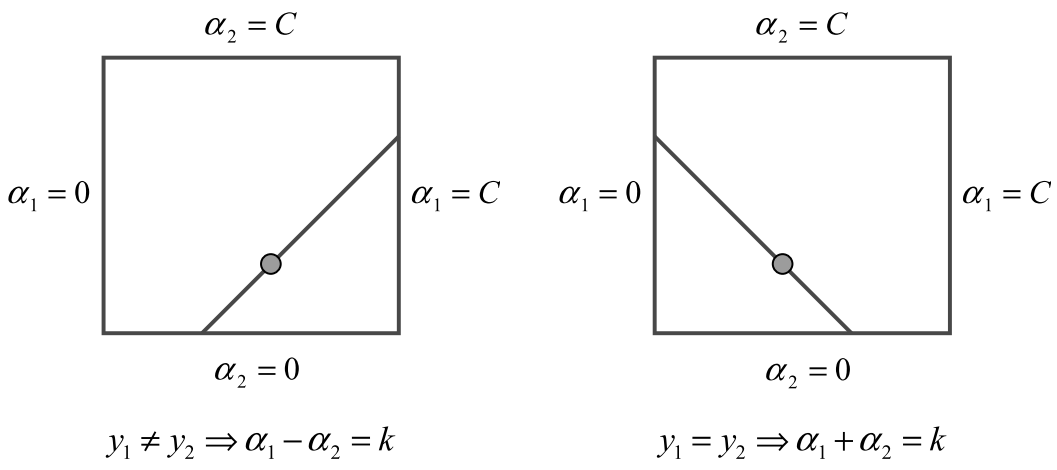
 假设先更新a2，再更新a1。a2的定义域下界设为L，上界设为H，则有：

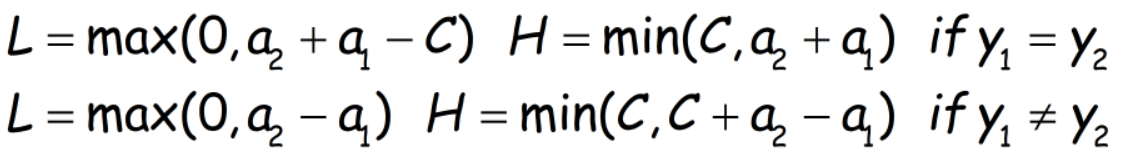
 设置以下2个中间变量：

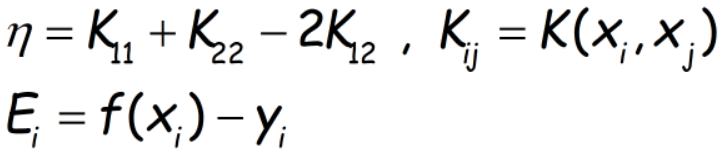
 这里经过很长的一段推导（将（1）式转化为只含有a2，求出a2后，使用以上2个中间变量代入），可以得到a2的更新值为：

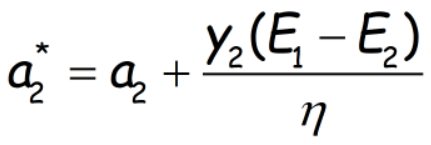
 记住，以上只针对η>0时成立（因为η为目标函数（1）式关于a2的二次项系数），再考虑到a2的定义域，a2的真实更新值可能需要截断：

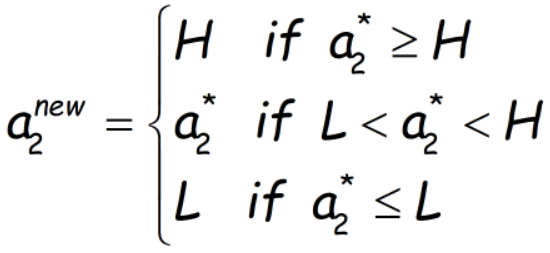
 当η≤0时，目标函数要么为一次函数（η=0），要么为开口向下的二次函数，则最小值必在边界（L或H处）取得。此时比较L和H处的函数值即可知a2的更新值。论文给出以下结论：

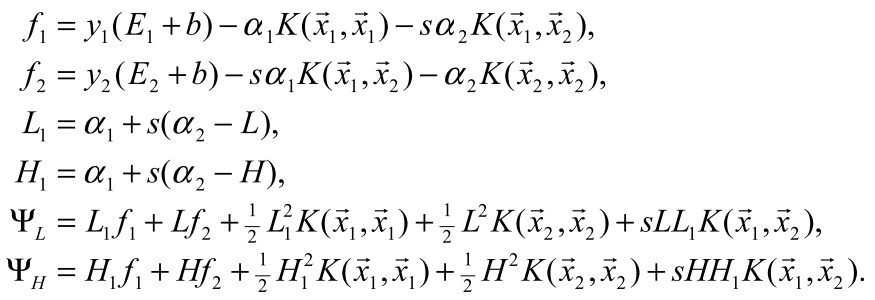
a1的更新由公式（3）确定（式（3）对于新、旧值都成立）：

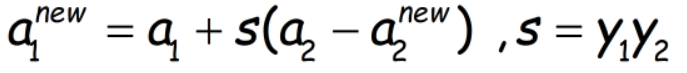
 注意上式中的a1，a2为没有更新前的旧值。