数据结构与算法之美学习笔记：第三讲

一、为什么需要复杂度分析？

1、测试结果非常依赖测试环境

Core i9
Core i3
在机器A上：a 代码执行的速度比 b 代码要快
在机器B上：b 代码执行的速度比 a 代码要快

2、测试结果受数据规模的影响很大

测试数据有序度不一样
测试数据规模太小不一样
所以、我们需要一个不用具体的测试数据来测试、就可以粗略地估算计算法的执行效率的方法
这就是我们今天要讲的时间、空间复杂度分析方法

二、大 O 复杂度表示法

1、如何在不用运行代码的情况下用"肉眼" 得到一段代码的执行时间呢？

读数据-运算-写数据
所有代码的执行时间T(n)与每行代码的执行次数n成正比

代码的执行时间=O(每行代码执行的次数总和)

大 O 复杂度表示法，实际并不具体表示代码真正的执行时间，而是表示代码执行时间随数据规模增长的变化趋势

渐进时间复杂度，简称时间复杂度

三、时间复杂度分析

1、只关注循环次数最多的一段代码

我们在分析一个算法、一段代码的时间复杂度的时候，也只关注循环执行次数最多的哪一行代码就可以

2、加法法则：总复杂度等于量级最大的那段代码的复杂度

总的时间复杂度就等于量级最大的那段代码的时间复杂度

3、乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

关键在于"熟练"。你只要多看案例，多分析，就能做到"无招胜有招"

四、几种常见时间复杂度实例分析

1、O(1)

 int i = 8;
 int j = 6;
 int sum = i + j;

O(1) 只是常量级时间复杂度的一种表示方法，并不是指只执行了一行代码。比如这段代码，即便有3行，它的时间复杂度也是O(1)
一般情况下，只要算法中不存在循环语句、递归语句，即使有成千上万行的代码，其时间复杂度也是Ο(1)

2. O(logn)、O(nlogn)

 i=1;
 while (i <= n)  {
   i = i * 2;
 }

i=1;
while (i <= n) {
i = i * 3;
}

如果一段代码的时间复杂度是 O(logn)，我们循环执行n遍，时间复杂度就是O(nlogn)
O(nlogn)这也是一种非常常见的算法时间复杂度，比如归并排序、快速排序的时间复杂度就是O(nlogn)

3. O(m+n)、O(m*n)

int cal(int m, int n) {
  int sum_1 = 0;
  int i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  int sum_2 = 0;
  int j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

针对这种情况，原来的加法法则就不正确了，
我们需要将加法规则改为：T1(m) + T2(n) = O(f(m) + g(n))
但是乘法法则继续有效：T1(m)*T2(n) = O(f(m) * f(n))。

五、空间复杂度分析

void print(int n) {
  int i = 0;
  int[] a = new int[n];
  for (i; i <n; ++i) {
    a[i] = i * i;
  }

  for (i = n-1; i >= 0; --i) {
    print out a[i]
  }
}

空间复杂度全称就是渐进式复杂度，表示算法的存储空间与数据规模之间的增长关系

O(1)、O(n)、O(n2 )，像 像 O(logn)、O(nlogn) 这样的对数阶复杂度平时用不到

六、小结

复杂度也叫渐进式复杂度，包括时间复杂度和空间复杂度，

用来分析算法执行效率与数据规模之间的增长关系

可以粗略地表示、越高阶复杂度的算法、执行效率越低。常见的复杂度并不多，

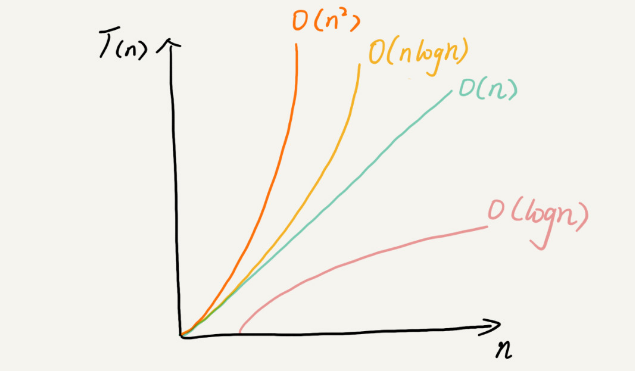
从低阶到高阶有：O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )

 

复杂度的分析并不难，关键在于多练

七、课后思考

1、题目

1、有人说，我们项目之前都会进行性能测试，再做代码的时间复杂度、空间复杂度分析是不是多此一举呢？
2、而且每段代码都分析一下时间复杂度、空间复杂度，是不是很浪费时间呢？
你怎么看待这个问题

2、答案

我不认为是多此一举，渐进时间，空间复杂度分析为我们提供了一个很好的理论分析的方向，并且它是宿主平台无关的，能够让我们对我们的程序或算法有一个大致的认识，让我们知道，比如在最坏的情况下程序的执行效率如何，同时也为我们交流提供了一个不错的桥梁，我们可以说，算法1的时间复杂度是O(n)，算法2的时间复杂度是O(logN)，这样我们立刻就对不同的算法有了一个“效率”上的感性认识。

当然，渐进式时间，空间复杂度分析只是一个理论模型，只能提供给粗略的估计分析，我们不能直接断定就觉得O(logN)的算法一定优于O(n), 针对不同的宿主环境，不同的数据集，不同的数据量的大小，在实际应用上面可能真正的性能会不同，个人觉得，针对不同的实际情况，进而进行一定的性能基准测试是很有必要的，比如在统一一批手机上(同样的硬件，系统等等)进行横向基准测试，进而选择适合特定应用场景下的最有算法。

综上所述，渐进式时间，空间复杂度分析与性能基准测试并不冲突，而是相辅相成的，但是一个低阶的时间复杂度程序有极大的可能性会优于一个高阶的时间复杂度程序，所以在实际编程中，时刻关心理论时间，空间度模型是有助于产出效率高的程序的，同时，因为渐进式时间，空间复杂度分析只是提供一个粗略的分析模型，因此也不会浪费太多时间，重点在于在编程时，要具有这种复杂度分析的思维