二值图像 b(x,y) = 1 表示前景部分，b(x,y) = 0 表示背景部分。其基本几何特性包括：‘
1 面积
对整个图像区域进行积分，使用零阶矩表示为 
。
2 位置
将图像区域看作一种均匀物质构成得平面，物体得质心即为区域中心；使用一阶矩表示如下：
，
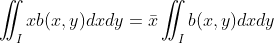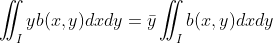，进一步改写得：
，
。
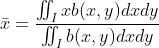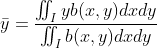3 朝向
假设物体沿某一方向比较长，其正交方向比较短，该方向定义为物体朝向。使用最小转动惯量来定义物体长轴，即寻找一条直线，使得物体上所有点到直线上距离平方和最小，定义如下：
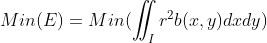， r 表示物体上点到直线的最小距离。
通过最小化 E，可以计算出物体朝向直线，具体如下：
1）假设二值图像朝向直线已知，使用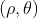 
定义为 
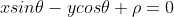，如下图：
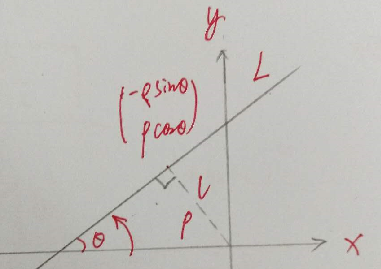
如上图所示，由于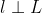 
，可以建立等式
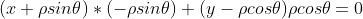，化简得
。
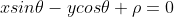2）对直线 L 上任意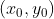点 
，以点 
作为参考点，建立参数方程如下：
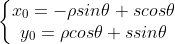，s 表示点 
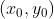距离参考点 的距离。
3）由于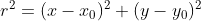 
，(x,y) 表示图像上的点，
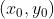表示直线上的点，将参数方程带入该等式，使得两个变量 
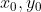简化为一个变量 s，如下：
，
，
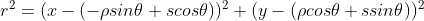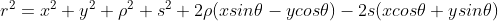对 s 求导，当导数为零时表示(x,y)到直线 L 上距离最近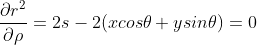 
，
计算得 
，将 s 带入 
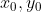得
，
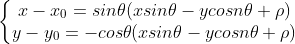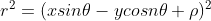，最终推导出转动惯量方程为
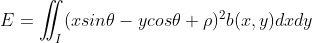，其中，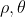
为待求解直线参数。
4）令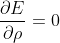 
，
，
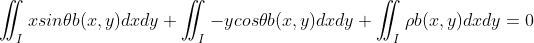将无关变量提出积分符号前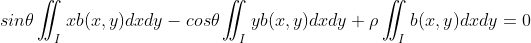
，
同时除以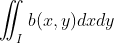 
得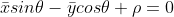 
，
由于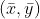 
为图像中心，则最小转动惯量对应得轴过图像中心。
5）通过 4）结论，直线 L 的确定可转换为对选择角度的求解，具体如下：
令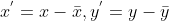 
，将图像上点绝对坐标转换为相对于图像中心的相对坐标，带入直线 L 方程得：
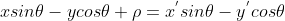，重新改写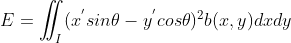 
，
当前 E 仅包含未知量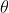 
，再次改写 
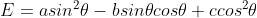，其中
，
，
，
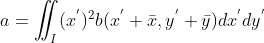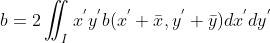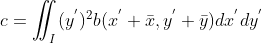使用倍角公式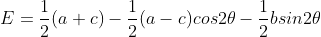 
，
，
，
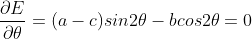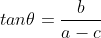通过以上分析，二值图像朝向直线为经过中心点，且满足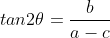 
的 直线，其中，a, b, c 为图像二阶矩。
4 形状
在分析二值图像朝向时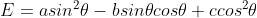，，该方程是关于 
的二次方程，
其系数 a, b, c 为可构成一个 2*2 矩阵，通过分析该矩阵的特征值与特征向量可以估计出二值图像的形状，具体如下：
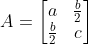，通过分析特征值与特征向量，可的如下结论：
1）较大特征值对应的特征向量方向即为二值图像朝向；
2）两个特征值相差越小，二值图像越接近圆形。
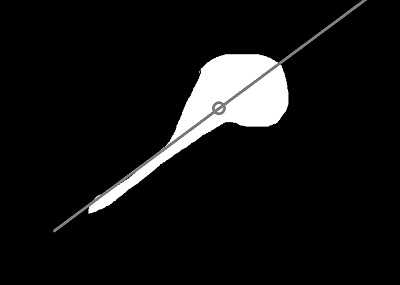
5 示例
以下给出代码，使用二阶矩计算二值图像朝向及形状，使用直线拟合计算二值图像朝向。可以发现，两种求朝向方案都可得到基本一致的结果。
1 cv::Mat img = cv::imread(str, IMREAD_GRAYSCALE); 2 cv::Mat img_show; 3 img.copyTo(img_show); 4 5 // 提取二值图像轮廓 6 std::vector<std::vector<cv::Point>> contours; 7 cv::findContours(img, contours, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_NONE); 8 if (contours.size() <= 0) 9 return; 10 11 // 只考虑每个图像上仅有一个二值图像 12 cv::Moments moms = cv::moments(cv::Mat(contours[0])); 13 double cx = moms.m10 / moms.m00; 14 double cy = moms.m01 / moms.m00; 15 double angle = atan2(moms.mu11 * 2., moms.mu20 - moms.mu02); 16 double tan = tanf(angle * .5); 17 double dx[2] = { -300., 300. }; 18 double dy[2] = { dx[0] * tan, dx[1] * tan }; 19 20 cv::Point pt1(cx + dx[0], cy + dy[0]); 21 cv::Point pt2(cx + dx[1], cy + dy[1]); 22 cv::circle(img_show, cv::Point(cx, cy), 10, cv::Scalar(125), 3); 23 cv::line(img_show, pt1, pt2, cv::Scalar(125), 3); 24 cv::imwrite("rst1.bmp", img_show); 25 26 // 计算二值图像圆形度 27 // 特征值比值（最大/最小）越接近1，圆形度越好 28 cv::Mat sym = cv::Mat::zeros(2, 2, CV_32FC1); 29 float *datasym = sym.ptr<float>(0); 30 datasym[0] = moms.mu20; 31 datasym[1] = moms.mu11; 32 datasym = sym.ptr<float>(1); 33 datasym[0] = moms.mu11; 34 datasym[1] = moms.mu02; 35 36 cv::Mat eg; 37 cv::eigen(sym, eg); 38 float e1 = eg.ptr<float>(0)[0]; 39 float e2 = eg.ptr<float>(1)[0]; 40 float circular = e1 / e2; 41 42 // 直线拟合 43 cv::Vec4f line_param; 44 cv::fitLine(contours[0], line_param, CV_DIST_L2, 0, .001, .001); 45 46 cv::Point pt0; 47 pt0.x = line_param[2]; 48 pt0.y = line_param[3]; 49 50 double k = line_param[1] / line_param[0]; 51 pt1.x = 0; 52 pt1.y = k * (0 - pt0.x) + pt0.y; 53 pt2.x = 480; 54 pt2.y = k * (480 - pt0.x) + pt0.y; 55 56 cv::line(img_show, pt1, pt2, cv::Scalar(50), 3); 57 cv::imwrite("rst2.bmp", img_show);
参考资料 Robot Vision Berthold Klaus Paul Horn