1 二元函数极值
对于单变量函数,使用一阶导数判断在某点上是否存在极值,使用二阶导数判断该点是极大值或者极小值。
对于二元函数,首先讨论二元二次函数极值情况,然后将结论推广到一般二元函数情形。
对二元二次函数 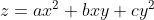 ,求偏导得并令其为 0 有
,求偏导得并令其为 0 有
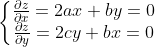 ,解方程组得
,解方程组得 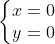 ,则函数 z 的临界点位于原点,进一步对函数 z 配方得
,则函数 z 的临界点位于原点,进一步对函数 z 配方得
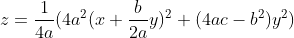 ,则系数
,则系数 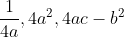 联合确定了原点为局部极大值或者局部极小值,具体如下:
联合确定了原点为局部极大值或者局部极小值,具体如下:
1)当  时,两平方项符号不一致,原点为鞍点(saddle point);
时,两平方项符号不一致,原点为鞍点(saddle point);
2)当 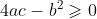 时,两平方项均为非负值,z 最终值取决于 a。
时,两平方项均为非负值,z 最终值取决于 a。
当 a > 0 时,原点为极小值点;当 a < 0 时,原点为极大值点;当 a = 0 时,无法判断;
对于一般二元函数 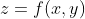 ,如果存在连续二阶偏导,在点
,如果存在连续二阶偏导,在点 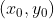 处,其一阶偏导满足关系
处,其一阶偏导满足关系 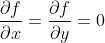 ,使用泰勒公式的二阶近似如下:
,使用泰勒公式的二阶近似如下:
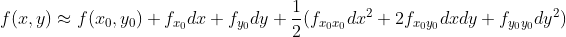 ,由于一阶偏导为零,进一步简化为:
,由于一阶偏导为零,进一步简化为:
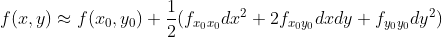 ,则函数 f(x,y) 在临界点
,则函数 f(x,y) 在临界点 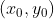 的极值特性取决于关系式
的极值特性取决于关系式
 ,该关系式与
,该关系式与 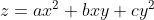 基本一致,则有如下结论:
基本一致,则有如下结论:
令 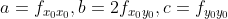 ,
,
1)当  时,两平方项符号不一致,临界点
时,两平方项符号不一致,临界点 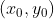 为鞍点(saddle point);
为鞍点(saddle point);
2)当 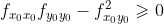 时,两平方项均为非负值,z 最终值取决于
时,两平方项均为非负值,z 最终值取决于 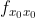 。
。
当 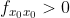 时,临界点
时,临界点 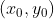 为极小值点;当
为极小值点;当 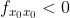 时,临界点
时,临界点 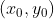 为极大值点;当
为极大值点;当 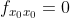 时,无法判断;
时,无法判断;
2 Hessian Matrix
定义函数 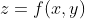 的 Hessian Matrix 为
的 Hessian Matrix 为 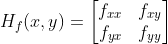 ,由于
,由于 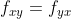 ,Hessian Matrix 可改写为
,Hessian Matrix 可改写为 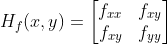 。
。
关系式  使用 Hessian Matrix 重写为
使用 Hessian Matrix 重写为  ,
,
使用 行列式 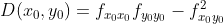 可得出类似结论:
可得出类似结论:
1)如果 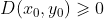 且
且 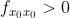 ,则
,则 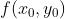 为局部极小值,f 向上凹;
为局部极小值,f 向上凹;
如果 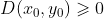 且
且 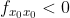 ,则
,则 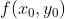 为局部极大值,f 向下凹;
为局部极大值,f 向下凹;
如果 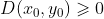 且
且 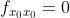 ,无法判断;
,无法判断;
2)如果 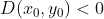 ,则
,则 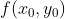 为鞍点(saddle point);
为鞍点(saddle point);
对 Hessian Matrix 进行特征值与特征向量分解,其特征值 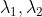 决定了二元二次函数性质,结论如下:
决定了二元二次函数性质,结论如下:
1)当 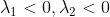 时,临界点
时,临界点 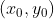 为局部极大值;
为局部极大值;
2)当 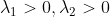 时,临界点
时,临界点 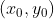 为局部极小值;
为局部极小值;
3)当 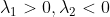 或
或 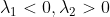 时, 临界点
时, 临界点 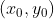 为 鞍点;
为 鞍点;
4)当 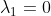 或
或  时,无法确定。
时,无法确定。
参考:多变量微积分 Prof. Denis Auroux