图像随机噪声

    图像灰度信息很难精确测量，一般情况下测量值总在真实值附近晃动，使用概率模型可以对该随机性建模，大致如下：

    1 概率密度函数

       1）随机变量 x 的概率密度函数 p(x) 定义为：当 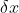 趋近于 0 时，在区间  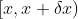上概率为 ；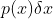

       2）随机变量 x 的期望（均值）定义为 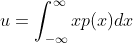，该均值为峰值中心位置；

       3）随机变量 x 的方差定义为 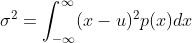，标准差为 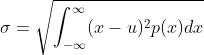，标准差是对概率分布宽度的度量。

    2 随机变量之和

       已知两个独立随机变量 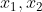 的概率密度分别为 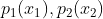，求随机变量 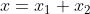的概率密度 p(x)，方法如下：

       1）在区间 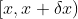上，给定 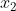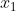， 的取值区间为 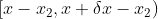，p(x) 发生的概率为 ；

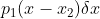       2）由于 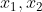的独立性，对于不同的 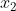，p(x) 发生的概率为 ；

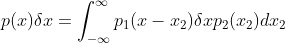       3）整理得 p(x) 的概率密度为 。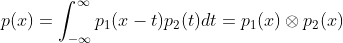

       4）通过统计直方图可以分别描述随机变量 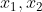  的离散分布，统计直方图的极限形式为随机变量  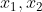 的概率密度函数。使用卷积可求解 p(x) 的概率密度函数。

           

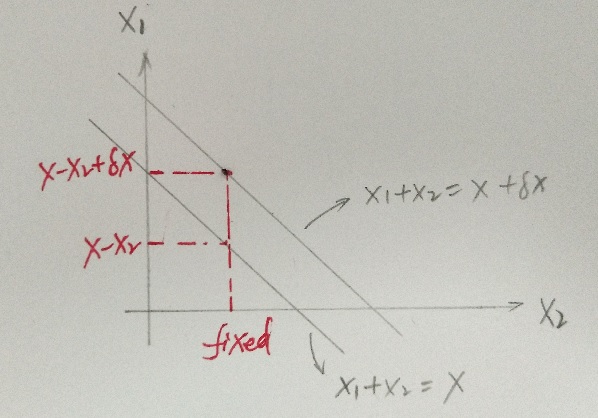
    3 多次测量求平均去噪

       通过多次测量，然后使用多次测量平均值可以降低随机变量噪声，理由如下：

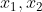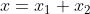       1）对于两个独立随机变量  ，随机变量  的方差满足 ；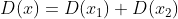

       2）线性变换随机变量，方差满足 ；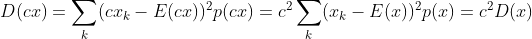

       3）对图像中同一点进行 N 次测量，其测量结果为 N 次随机变量 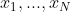，且各个随机变量均值与方差都为 ;

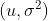            随机变量 x 方差为 ；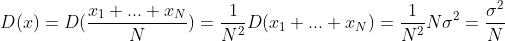

            随机变量 x 标准差为 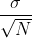，标准差表征概率分布宽度，当使用多次测量求平均可以降低随机变量波动范围，从而实现去噪。

    参考资料 Robot Vision  Berthold Klaus Paul Horn