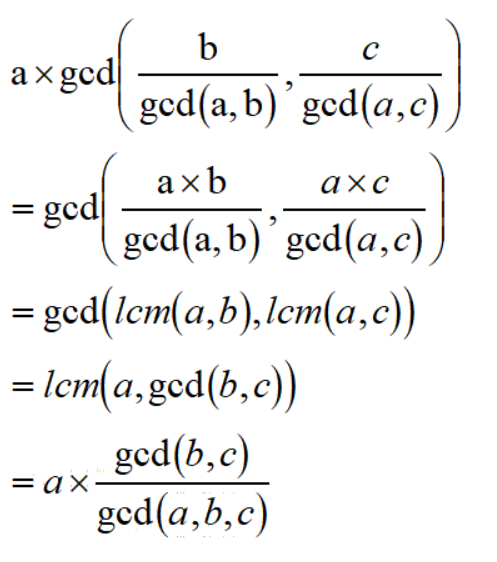A.Orac and Factors
思维:原数字+最小质因子(除1以外)+(k-1)*2
B. Orac and Models
题意:
给n长度的数组,问下标为倍数,同时满足前者小于后者的最大个数是多少
思路:
dfs,搜1~n/2。
因为自己nt,dfs内部写错。wa自闭了
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define il inline
#define it register int
#define inf 0x3f3f3f3f
#define lowbit(x) (x)&(-x)
#define pii pair<int,int>
#define mak(n,m) make_pair(n,m)
#define mem(a,b) memset(a,b,sizeof(a))
#define mod 1000000007
const int maxn=2e5+10;
const int mo=1e9;
ll ksm(ll a,ll b){if(b<0)return 0;ll ans=1;while(b){if(b&1)ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans;}
int t;
int n,m;
int a[maxn],maxx;
void dfs(int ge,int zhi){
maxx=max(maxx,zhi);
if(ge*2>n){
return;
}
for(it i=2;i<=n/ge;i++){
if(a[ge]<a[ge*i]){dfs(ge*i,zhi+1);}
}
}
int main(){
scanf("%d",&t);
while(t--){
scanf("%d",&n);
for(it i=1;i<=n;i++){
scanf("%d",&a[i]);
}
maxx=1;
for(it i=1;i<=n/2;i++){
dfs(i,1);
}
printf("%d
",maxx);
}
return 0;
}
C - Orac and LCM
题意:
给长度为n的数组,每个数ai对后面的每个数aj进行LCM(ai,aj),之后求这些LCM的gcd是多少
思路:
把每个数的质因子的种类和个数提取出来,然后如果这个这些 相同的质因子 分别来自不同数字的n-2个以上的,就是gcd之和
如果是n-1个数字,取最小的一位,如果是n个数字,取第二小的一位
用样例解释一下,10, 24, 40, 80
分别是
2 5
2 2 2 3
2 2 2 5
2 2 2 2 5
2质因子个数是 1 3 3 4,因为有4个,所以是取第二个小的3,2^3=8
3质因子个数是 0 1 0 0,取第二个小的,因为第二是0,so continue
5质因子个数是 1 0 1 1,取第二个小的 1,8*5^1=40
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define il inline
#define it register int
#define inf 0x3f3f3f3f
#define lowbit(x) (x)&(-x)
#define pii pair<int,int>
#define mak(n,m) make_pair(n,m)
#define mem(a,b) memset(a,b,sizeof(a))
#define mod 1000000007
const int maxn=1e5+10;
const int mo=1e9;
ll ksm(ll a,ll b){if(b<0)return 0;ll ans=1;while(b){if(b&1)ans=ans*a;a=a*a;b>>=1;}return ans;}
int a[maxn];
int n,m;
vector<int>v[maxn];
int main(){
scanf("%d",&n);
for(it i=0;i<n;i++){
scanf("%d",&a[i]);
}
map<int,int>mp;
map<int,int>pos;
int t=1;
for(it i=0;i<n;i++){
int kk=sqrt(a[i]),k=a[i];
for(it i=2;i<=kk;i++){
if(k%i==0){
int ci=1;k/=i;
while(k%i==0){
ci++;k/=i;
}
if(mp[i]==0){pos[t]=i;mp[i]=t++;}
v[mp[i]].push_back(ci);
}
}
if(k!=1){
if(mp[k]==0){pos[t]=k;mp[k]=t++;}
int ci=1;
v[mp[k]].push_back(ci);
}
}
ll ans=(ll)1;
for(it i=1;i<t;i++){
int z=pos[i],l=v[i].size();
if(n-l>=2){continue;}
sort(v[i].begin(),v[i].end());
if((n-l)==1){
ans*=(ll)(ksm((ll)z,(ll)v[i][0]));
}
else if((n-l)==0){
ans*=(ll)(ksm((ll)z,(ll)v[i][1]));
}
}
printf("%lld
",ans);
return 0;
}
D - Orac and Medians
题意:
给一个n长度的数组,再给一个k,有无限操作,操作是选择一段数组,长度为l,把 这段数组里的数字 全部替代成第(l+1)/2大小的数字,问能不能把数组全部变成k
思路:
其实这题就是考一个思维,第一个条件是数组要有k,再特判一下只有一个数字的数组情况。然后遍历一遍,大于等于k的数字有没有距离小于3的
举个例子就是 3 1 4 1 1 1,全部变成3,先找3 1 4,这样就变成了3 3 3 1 1 1,然后找3 3 1 变成 3 3 3 3 1 1,再找3 3 3 3 1 1 这样就是3 3 3 3 3 3 了
如果是3 4这种贴着的,可以直接变成3 3
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define ull unsigned long long
#define il inline
#define it register int
#define inf 0x3f3f3f3f
#define lowbit(x) (x)&(-x)
#define pii pair<int,int>
#define mak(n,m) make_pair(n,m)
#define mem(a,b) memset(a,b,sizeof(a))
#define mod 1000000007
const int maxn=1e5+10;
const int mo=1e9;
ll ksm(ll a,ll b){if(b<0)return 0;ll ans=1;while(b){if(b&1)ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans;}
int t;
int n,m;
int a[maxn];
int main(){
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&m);
int ff=1;
for(it i=1;i<=n;i++){
scanf("%d",&a[i]);
if(a[i]==m){ff=0;}
}
if(ff){printf("no
");continue;}
if(n==1 && a[1]==m){
printf("yes
");continue;
}
else if(n==1&& a[1]!=m){
printf("no
");continue;
}
int f=1;
int pos=-2;
for(it i=1;i<=n;i++){
if(a[i]>=m){
if(abs(i-pos)<=2){f=0;break;}
pos=i;
}
}
if(!f){printf("yes
");}
else{printf("no
");}
}
return 0;
}
C题的另一种写法