计算机组成原理笔记（二）

我的博客： https://www.luozhiyun.com/

浮点数和定点数

我们先来看一个问题，在Chrome浏览器里面通过开发者工具，打开浏览器里的Console，在里面输入“0.3 + 0.6”：

>>> 0.3 + 0.6
0.8999999999999999

下面我们来一步步解释，为什么会这样。

定点数

如果我们用32个比特表示整数，用4个比特来表示0～9的整数，那么32个比特就可以表示8个这样的整数。

然后我们把最右边的2个0～9的整数，当成小数部分；把左边6个0～9的整数，当成整数部分。这样，我们就可以用32个比特，来表示从0到999999.99这样1亿个实数了。

这种用二进制来表示十进制的编码方式，叫作BCD编码。这种小数点固定在某一位的方式，我们也就把它称为定点数。

缺点：
第一，这样的表示方式有点“浪费”。本来32个比特我们可以表示40亿个不同的数，但是在BCD编码下，只能表示1亿个数。
第二，这样的表示方式没办法同时表示很大的数字和很小的数字。

浮点数

我们在表示一个很大的数的时候，通常可以用科学计数法来表示。

在计算机里，我也可以用科学计数法来表示实数。浮点数的科学计数法的表示，有一个IEEE的标准，它定义了两个基本的格式。一个是用32比特表示单精度的浮点数，也就是我们常常说的float或者float32类型。另外一个是用64比特表示双精度的浮点数，也就是我们平时说的double或者float64类型。

单精度

单精度的32个比特可以分成三部分。

第一部分是一个符号位，用来表示是正数还是负数。我们一般用s来表示。在浮点数里，我们不像正数分符号数还是无符号数，所有的浮点数都是有符号的。

接下来是一个8个比特组成的指数位。我们一般用e来表示。8个比特能够表示的整数空间，就是0～255。我们在这里用1～254映射到-126～127这254个有正有负的数上。

最后，是一个23个比特组成的有效数位。我们用f来表示。综合科学计数法，我们的浮点数就可以表示成下面这样：

$(-1)^s×1.f×2e$

特殊值的表示：

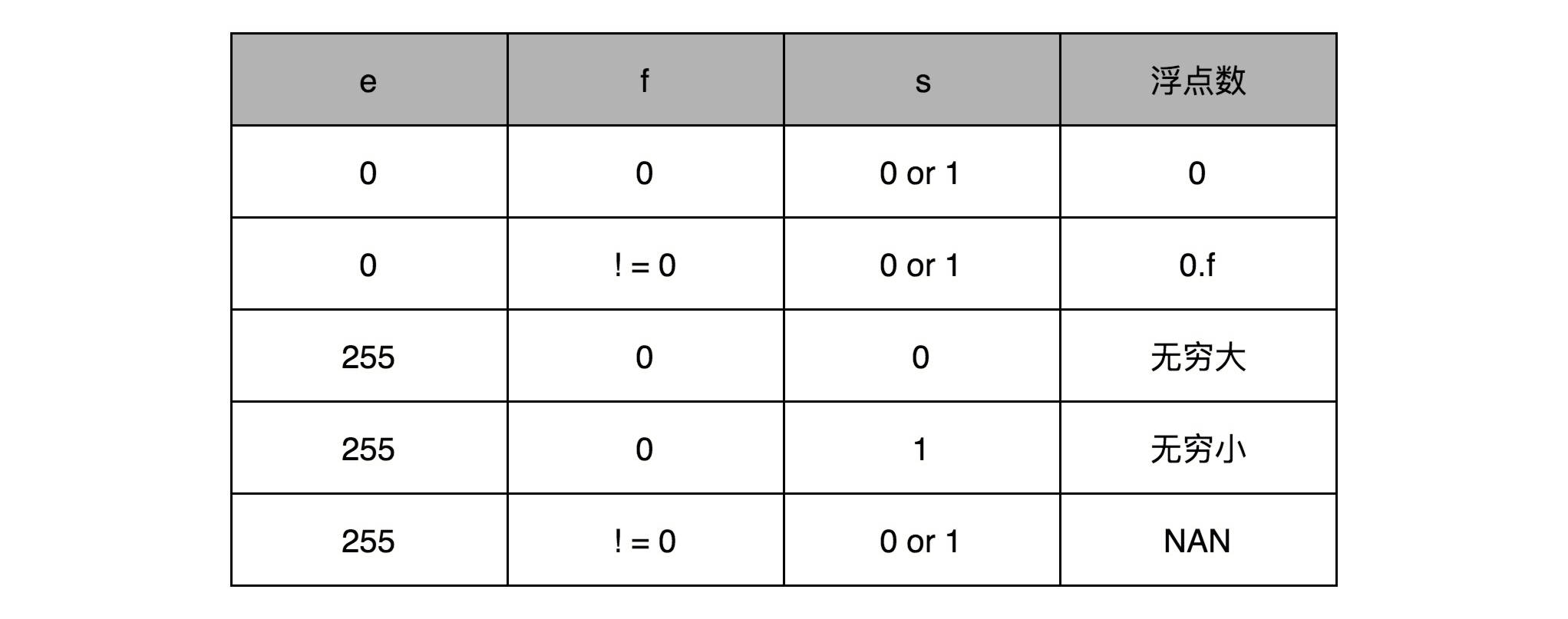
以0.5为例子。0.5的符号为s应该是0，f应该是0，而e应该是-1，也就是

$0.5= (-1)^0×1.0×2{-1}=0.5$，对应的浮点数表示，就是32个比特。

不考虑符号的话，浮点数能够表示的最小的数和最大的数，差不多是$1.17×10^{{-38}$和$3.40×10}{38}$。

回到我们最开头，为什么我们用0.3 + 0.6不能得到0.9呢？这是因为，浮点数没有办法精确表示0.3、0.6和0.9。

浮点数的二进制转化

我们输入一个任意的十进制浮点数，背后都会对应一个二进制表示。

比如：9.1，那么，首先，我们把这个数的整数部分，变成一个二进制。这里的9，换算之后就是1001。

接着，我们把对应的小数部分也换算成二进制。和整数的二进制表示采用“除以2，然后看余数”的方式相比，小数部分转换成二进制是用一个相似的反方向操作，就是乘以2，然后看看是否超过1。如果超过1，我们就记下1，并把结果减去1，进一步循环操作。在这里，我们就会看到，0.1其实变成了一个无限循环的二进制小数，0.000110011。这里的“0011”会无限循环下去。

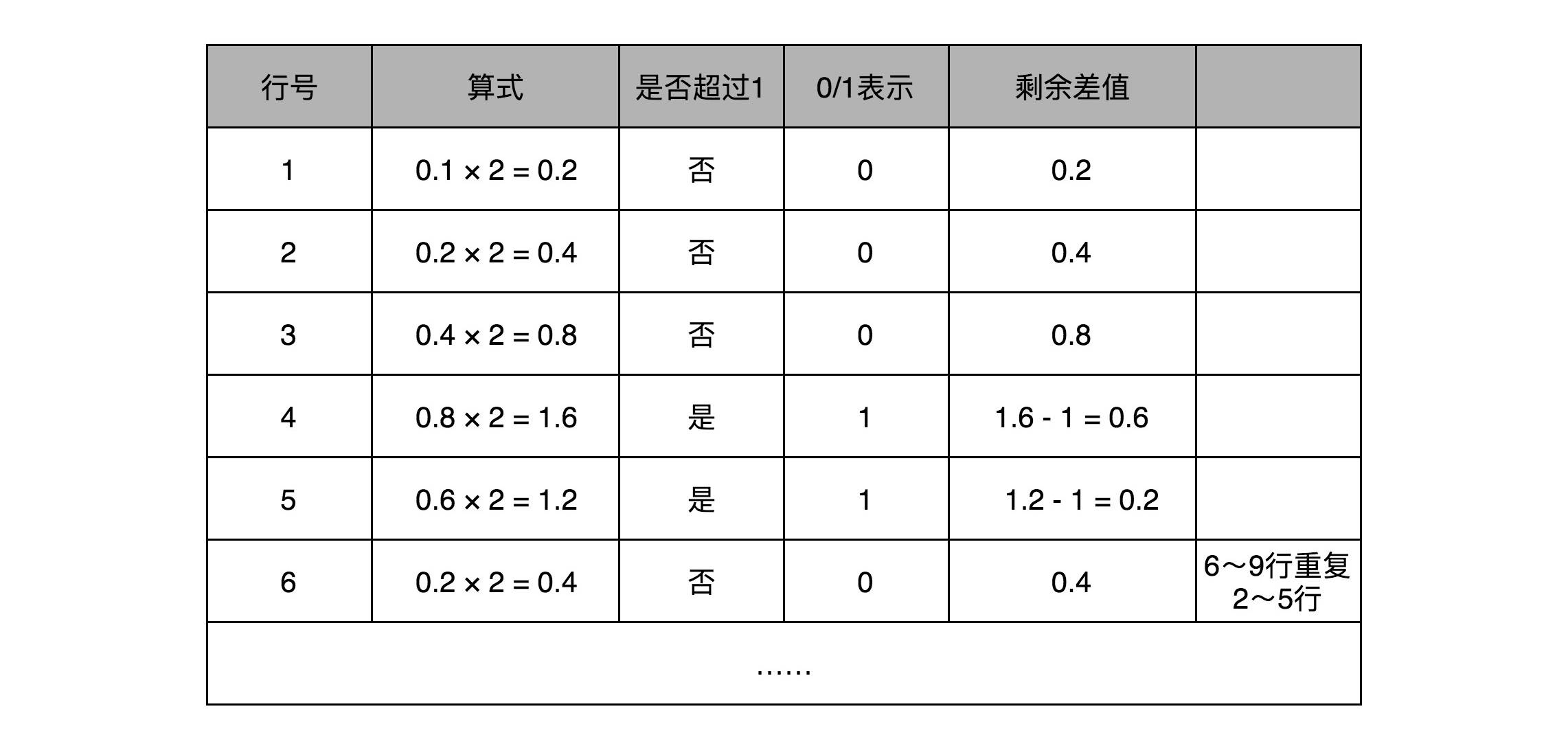
结果就是：$1.0010$$0011$$0011… × 2^3$

这里的符号位s = 0，对应的有效位f=001000110011…。因为f最长只有23位，那这里“0011”无限循环，最多到23位就截止了。于是，f=00100011001100110011 001。最后的一个“0011”循环中的最后一个“1”会被截断掉。

对应的指数为e，代表的应该是3。因为指数位有正又有负，所以指数位在127之前代表负数，之后代表正数，那3其实对应的是加上127的偏移量130，转化成二进制，就是130，对应的就是指数位的二进制，表示出来就是10000010。

最终得到的二进制表示就变成了：

010000010 0010 0011001100110011 001

如果我们再把这个浮点数表示换算成十进制， 实际准确的值是9.09999942779541015625。

浮点数的加法和精度损失

浮点数的加法是：先对齐、再计算。

那我们在计算0.5+0.125的浮点数运算的时候，首先要把两个的指数位对齐，也就是把指数位都统一成两个其中较大的-1。对应的有效位1.00…也要对应右移两位，因为f前面有一个默认的1，所以就会变成0.01。然后我们计算两者相加的有效位1.f，就变成了有效位1.01，而指数位是-1，这样就得到了我们想要的加法后的结果。

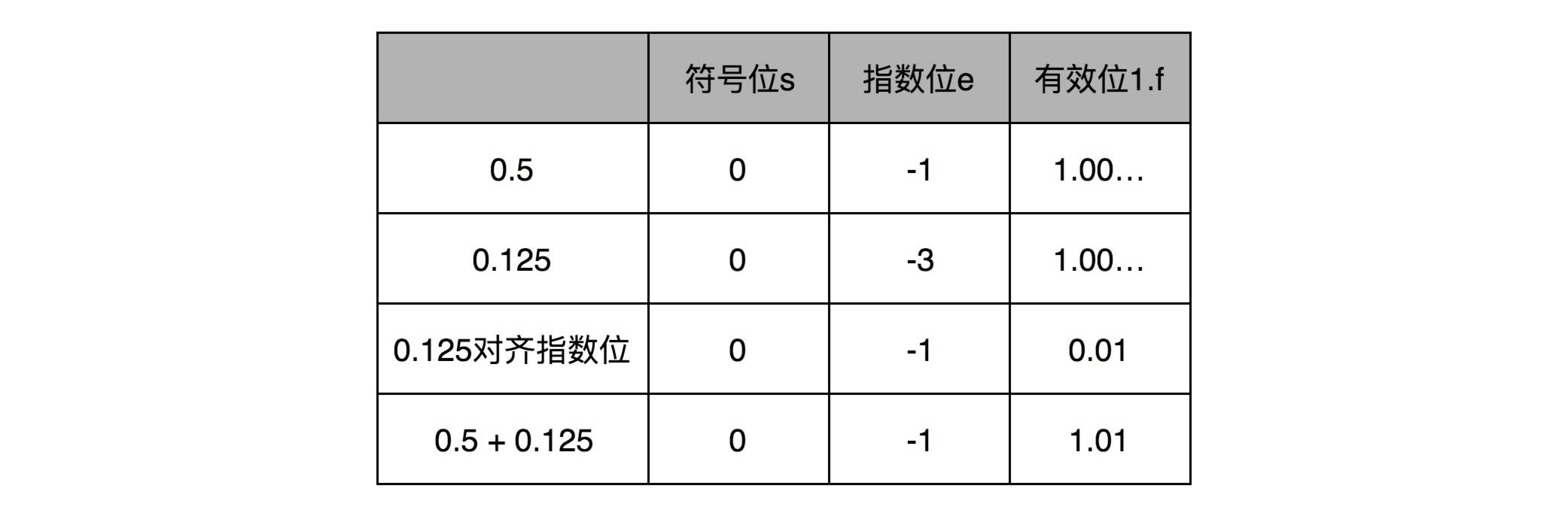
其中指数位较小的数，需要在有效位进行右移，在右移的过程中，最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。

指令周期（Instruction Cycle）

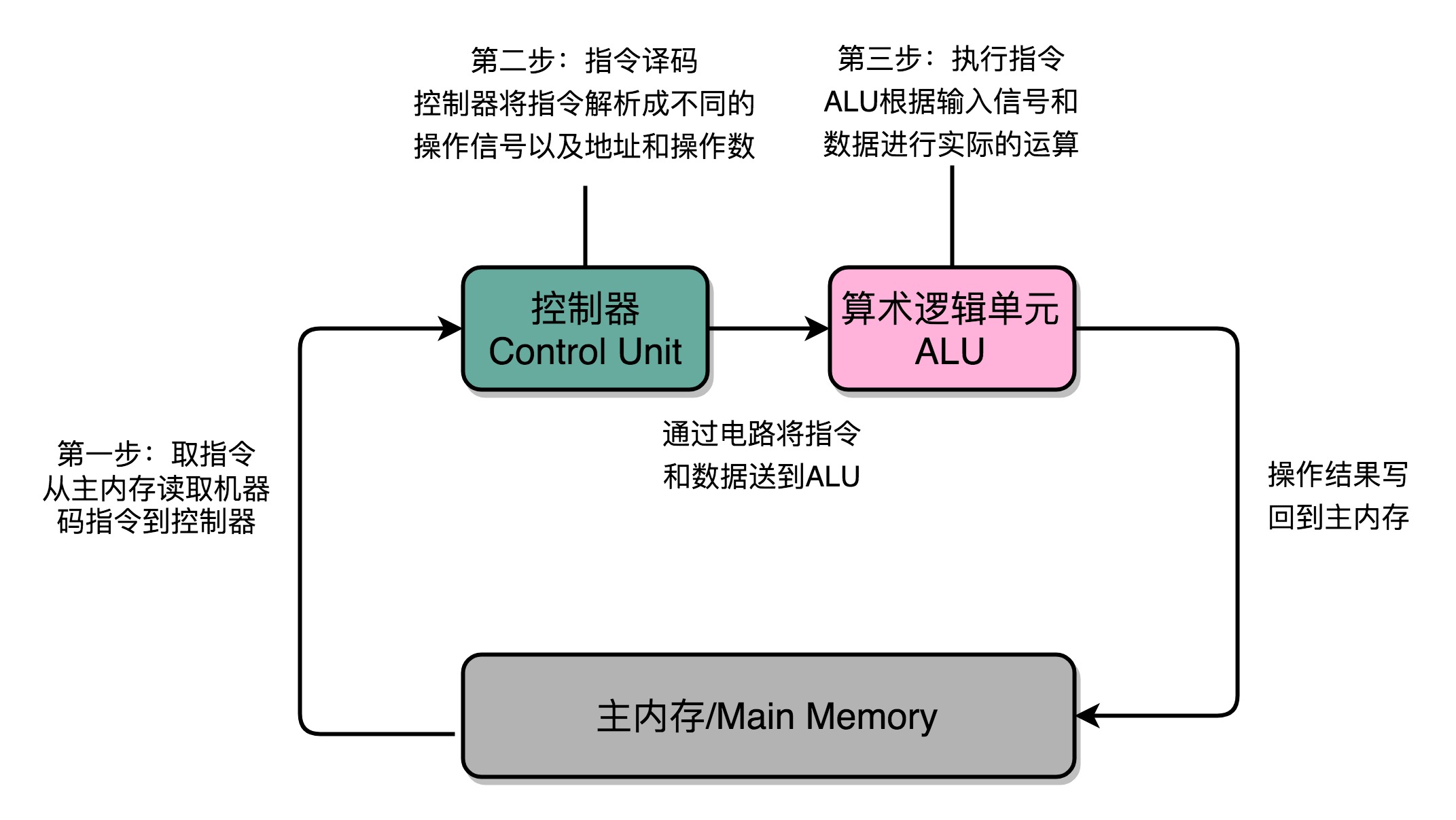
计算机每执行一条指令的过程，可以分解成这样几个步骤。

1. Fetch（取得指令），也就是从PC寄存器里找到对应的指令地址，根据指令地址从内存里把具体的指令，加载到指令寄存器中，然后把PC寄存器自增，好在未来执行下一条指令。
2. Decode（指令译码），也就是根据指令寄存器里面的指令，解析成要进行什么样的操作，是R、I、J中的哪一种指令，具体要操作哪些寄存器、数据或者内存地址。
3. Execute（执行指令），也就是实际运行对应的R、I、J这些特定的指令，进行算术逻辑操作、数据传输或者直接的地址跳转。

Fetch - Decode - Execute循环称之为指令周期（Instruction Cycle）。

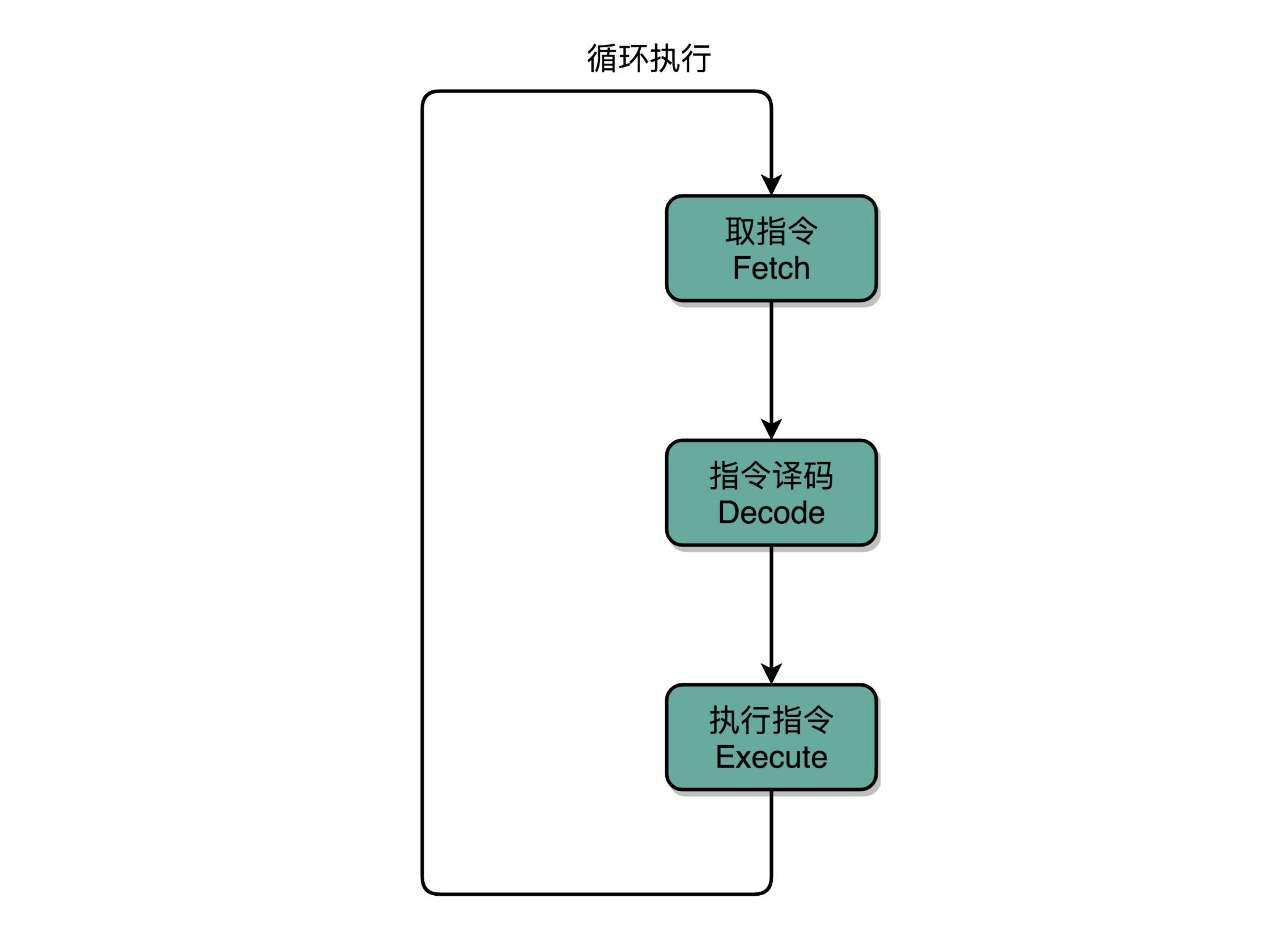
在取指令的阶段，我们的指令是放在存储器里的，实际上，通过PC寄存器和指令寄存器取出指令的过程，是由控制器（Control Unit）操作的。指令的解码过程，也是由控制器进行的。一旦到了执行指令阶段，无论是进行算术操作、逻辑操作的R型指令，还是进行数据传输、条件分支的I型指令，都是由算术逻辑单元（ALU）操作的，也就是由运算器处理的。不过，如果是一个简单的无条件地址跳转，那么我们可以直接在控制器里面完成，不需要用到运算器。

时序逻辑电路

有一些电路，只需要给定输入，就能得到固定的输出。这样的电路，我们称之为组合逻辑电路（Combinational Logic Circuit）。

时序逻辑电路有以下几个特点：

1. 自动运行，时序电路接通之后可以不停地开启和关闭开关，进入一个自动运行的状态。
2. 存储。通过时序电路实现的触发器，能把计算结果存储在特定的电路里面，而不是像组合逻辑电路那样，一旦输入有任何改变，对应的输出也会改变。
3. 时序电路使得不同的事件按照时间顺序发生。

最常见的就是D触发器，电路的输出信号不单单取决于当前的输入信号，还要取决于输出信号之前的状态。

PC寄存器

PC寄存器就是程序计数器。

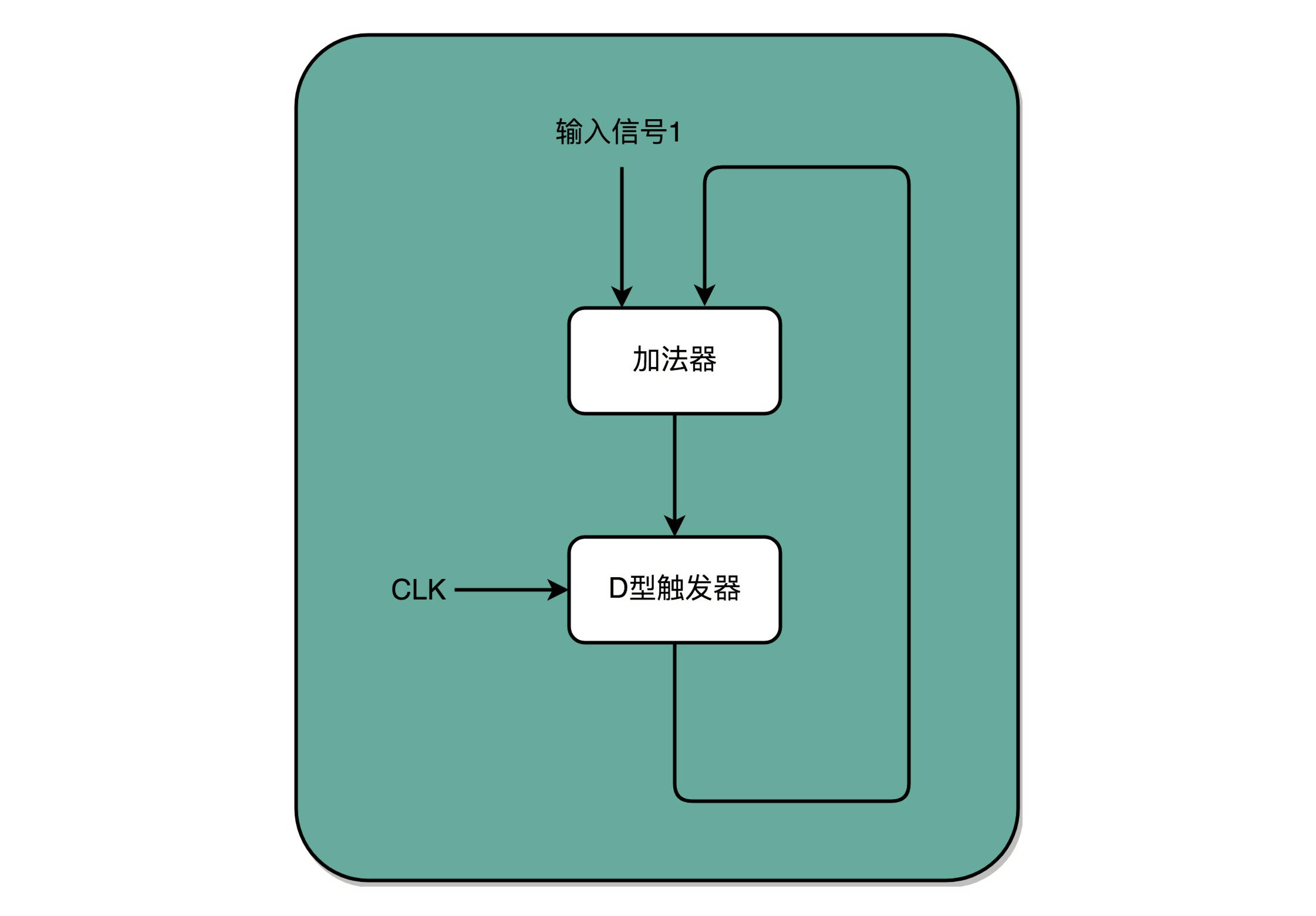
加法器的两个输入，一个始终设置成1，另外一个来自于一个D型触发器A。我们把加法器的输出结果，写到这个D型触发器A里面。于是，D型触发器里面的数据就会在固定的时钟信号为1的时候更新一次。

这样，我们就有了一个每过一个时钟周期，就能固定自增1的自动计数器了。

最简单的CPU流程

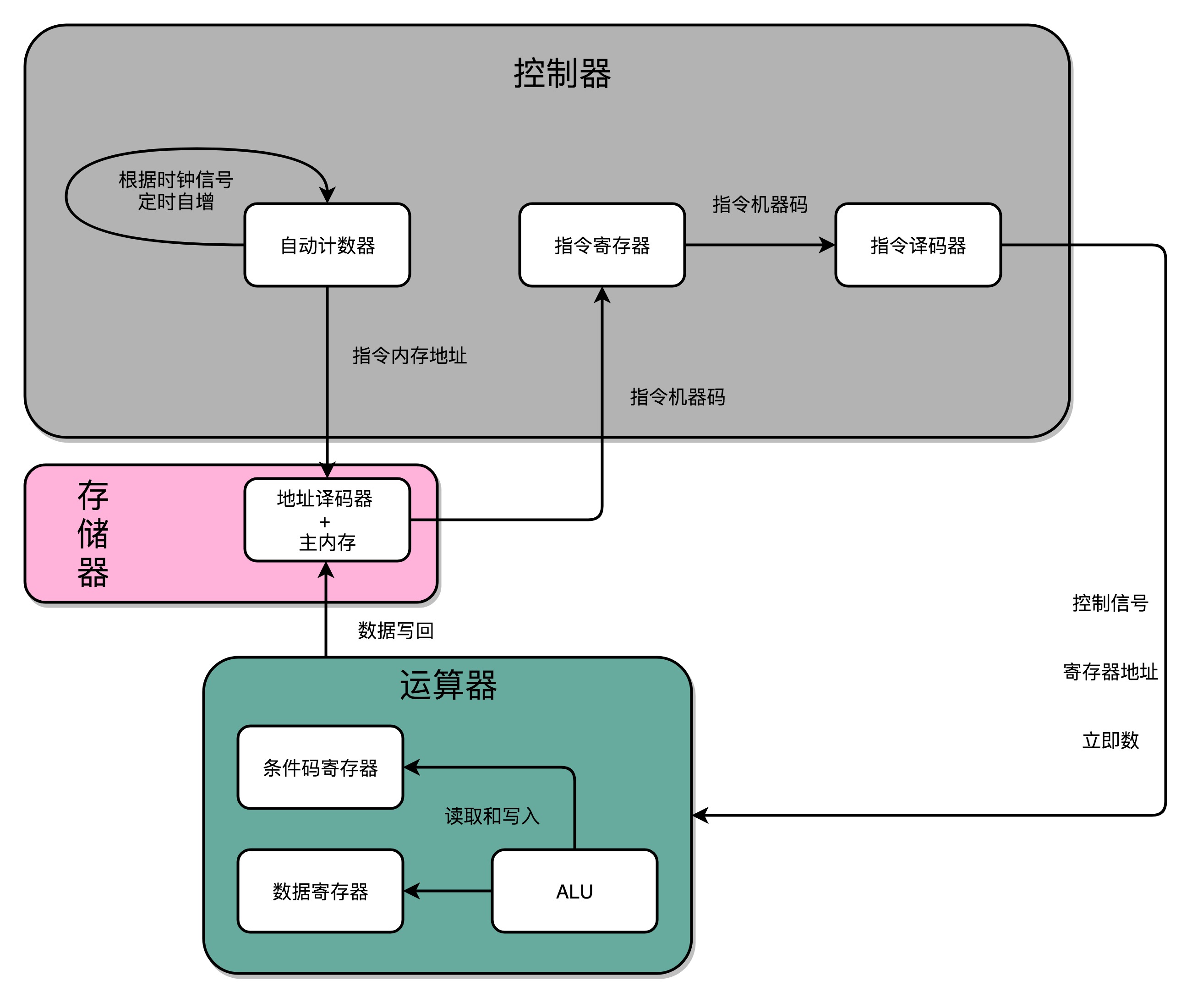
1. 首先，有一个自动计数器会随着时钟主频不断地自增，来作为我们的PC寄存器。
2. 在这个自动计数器的后面，我们连上一个译码器（用来寻址，将指令内存地址转换成指令）。译码器还要同时连着我们通过大量的D触发器组成的内存。
3. 自动计数器会随着时钟主频不断自增，从译码器当中，找到对应的计数器所表示的内存地址，然后读取出里面的CPU指令。
4. 读取出来的CPU指令会通过我们的CPU时钟的控制，写入到一个由D触发器组成的寄存器，也就是指令寄存器当中。
5. 在指令寄存器后面，我们可以再跟一个译码器。这个译码器不再是用来寻址的了，而是把我们拿到的指令，解析成opcode和对应的操作数。
6. 当我们拿到对应的opcode和操作数，对应的输出线路就要连接ALU，开始进行各种算术和逻辑运算。对应的计算结果，则会再写回到D触发器组成的寄存器或者内存当中。

指令流水线

指令流水线指的是把一个指令拆分成一个一个小步骤，从而来减少单条指令执行的“延时”。通过同时在执行多条指令的不同阶段，我们提升了CPU的“吞吐率”。

如果我们把一个指令拆分成“取指令-指令译码-执行指令”这样三个部分，那这就是一个三级的流水线。如果我们进一步把“执行指令”拆分成“ALU计算（指令执行）-内存访问-数据写回”，那么它就会变成一个五级的流水线。

五级的流水线，就表示我们在同一个时钟周期里面，同时运行五条指令的不同阶段。

我们可以看这样一个例子。我们顺序执行这样三条指令。

1. 一条整数的加法，需要200ps。
2. 一条整数的乘法，需要300ps。
3. 一条浮点数的乘法，需要600ps

如果我们是在单指令周期的CPU上运行，最复杂的指令是一条浮点数乘法，那就需要600ps。那这三条指令，都需要600ps。三条指令的执行时间，就需要1800ps。

如果我们采用的是6级流水线CPU，每一个Pipeline的Stage都只需要100ps。那么，在这三个指令的执行过程中，在指令1的第一个100ps的Stage结束之后，第二条指令就开始执行了。在第二条指令的第一个100ps的Stage结束之后，第三条指令就开始执行了。这种情况下，这三条指令顺序执行所需要的总时间，就是800ps。那么在1800ps内，使用流水线的CPU比单指令周期的CPU就可以多执行一倍以上的指令数。

流水线设计CPU的风险

1. 结构冒险

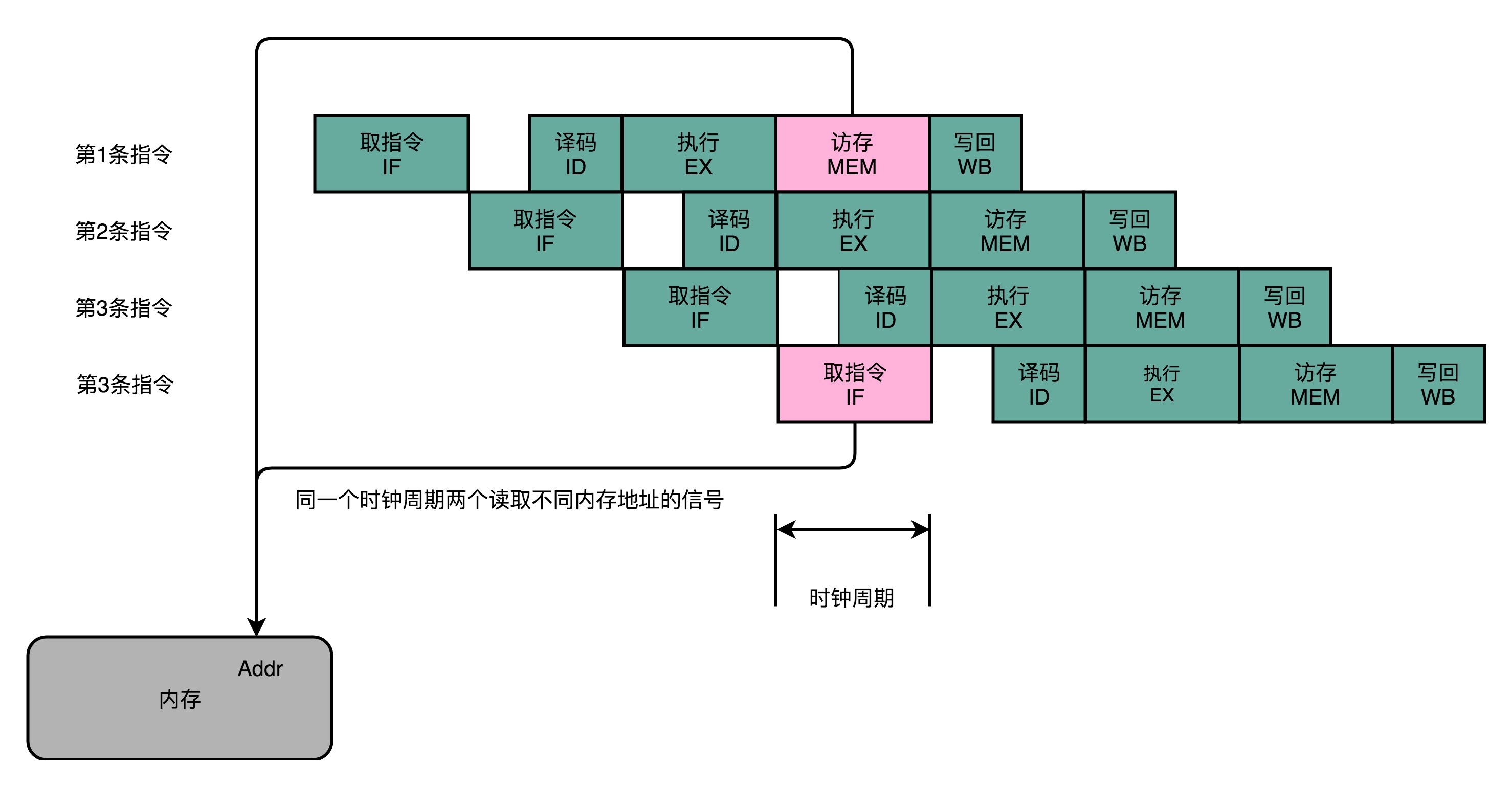
可以看到，在第1条指令执行到访存（MEM）阶段的时候，流水线里的第4条指令，在执行取指令（Fetch）的操作。访存和取指令，都要进行内存数据的读取。但是内存在一个时钟周期是没办法都做的。

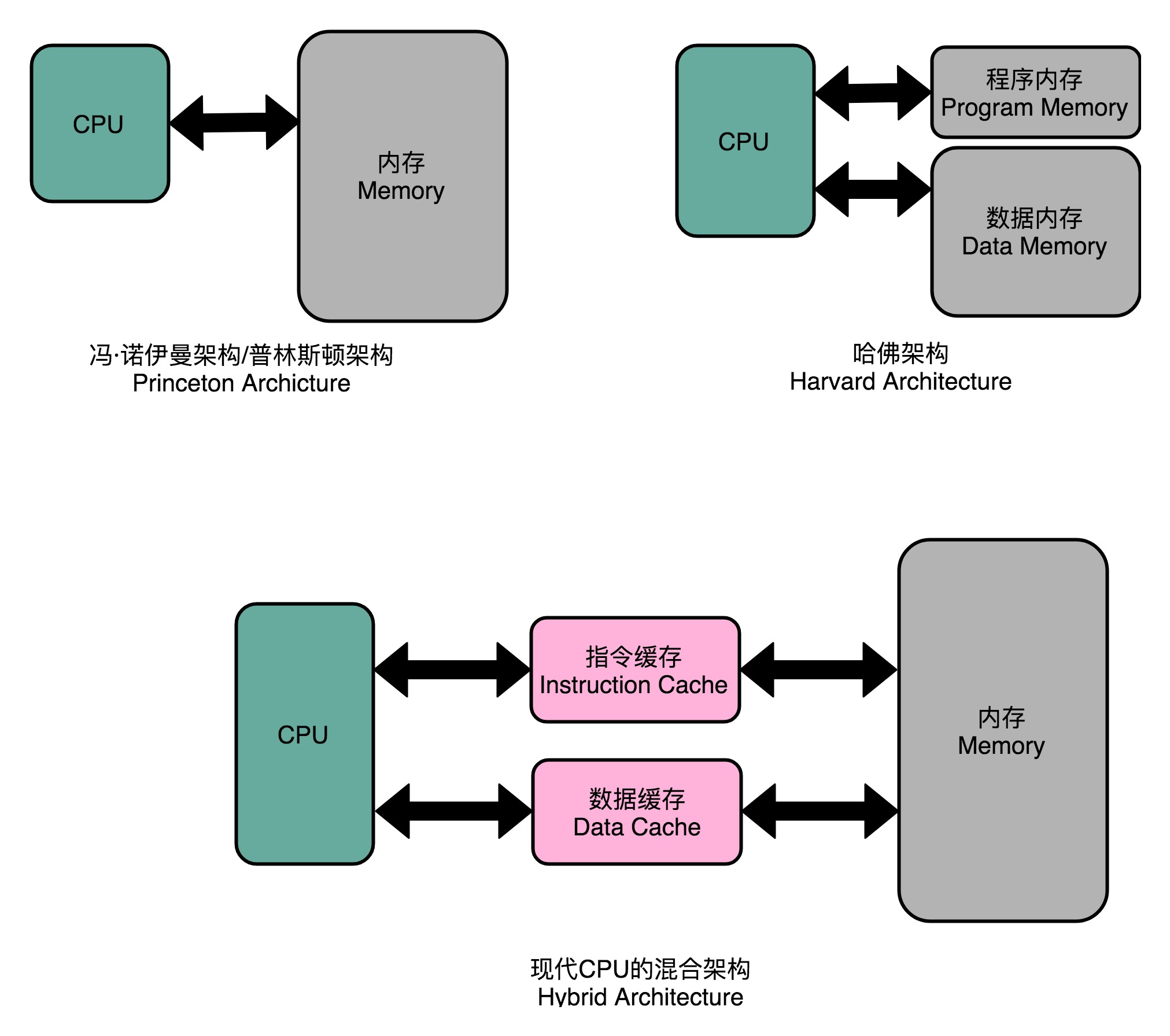
解决办法：在高速缓存层面拆分成指令缓存和数据缓存

在CPU内部的高速缓存部分进行了区分，把高速缓存分成了指令缓存（Instruction Cache）和数据缓存（Data Cache）两部分。

2. 数据冒险
   先写后读

int main() {
  int a = 1;
  int b = 2;
  a = a + 2;
  b = a + 3;
}

这里需要保证a和b的值先赋，然后才能进行准确的运算。这个先写后读的依赖关系，我们一般被称之为数据依赖，也就是Data Dependency。

先读后写

int main() {
  int a = 1;
  int b = 2;
  a = b + a;
  b = a + b;
}

这里我们先要读出a = b+a，然后才能正确的写入b的值。这个先读后写的依赖，一般被叫作反依赖，也就是Anti-Dependency。

写后再写

int main() {
  int a = 1;
  a = 2;
}

很明显，两个写入操作不能乱，要不然最终结果就是错误的。这个写后再写的依赖，一般被叫作输出依赖，也就是Output Dependency。

解决办法：流水线停顿（Pipeline Stall）

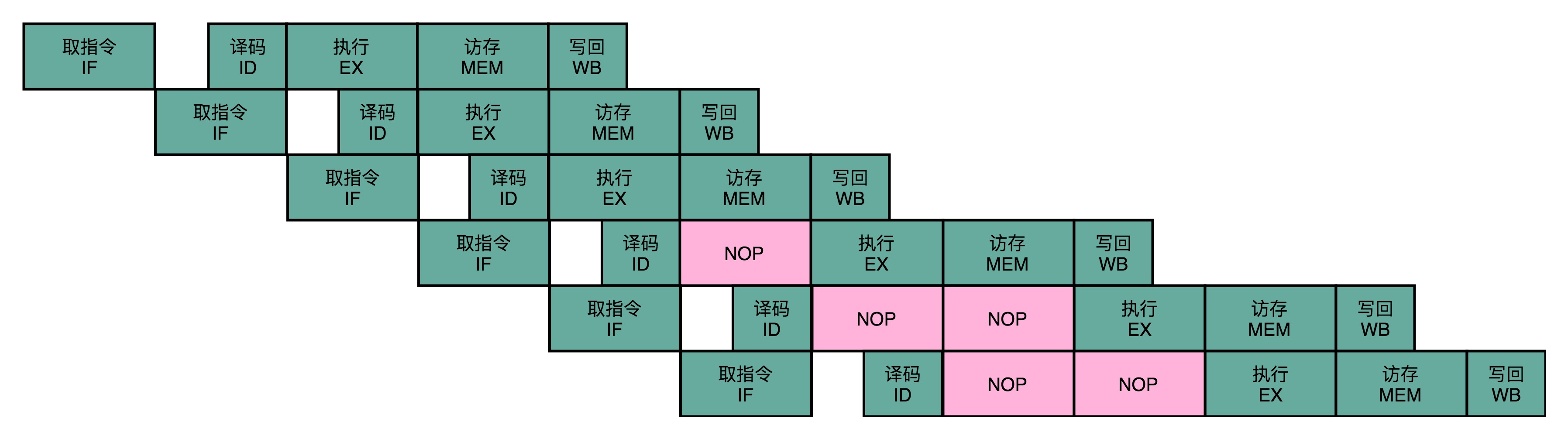
如果我们发现了后面执行的指令，会对前面执行的指令有数据层面的依赖关系，那最简单的办法就是“再等等”。我们在进行指令译码的时候，会拿到对应指令所需要访问的寄存器和内存地址。

在实践过程中，在执行后面的操作步骤前面，插入一个NOP操作，也就是执行一个其实什么都不干的操作。

3. 控制冒险

在执行的代码中，一旦遇到 if…else 这样的条件分支，或者 for/while 循环的时候会发生类似cmp比较指令、jmp和jle这样的条件跳转指令。

在jmp指令发生的时候，CPU可能会跳转去执行其他指令。jmp后的那一条指令是否应该顺序加载执行，在流水线里面进行取指令的时候，我们没法知道。要等jmp指令执行完成，去更新了PC寄存器之后，我们才能知道，是否执行下一条指令，还是跳转到另外一个内存地址，去取别的指令。

解决办法：
缩短分支延迟
条件跳转指令其实进行了两种电路操作。
第一种，是进行条件比较。
第二种，是进行实际的跳转，也就是把要跳转的地址信息写入到PC寄存器。无论是opcode，还是对应的条件码寄存器，还是我们跳转的地址，都是在指令译码（ID）的阶段就能获得的。而对应的条件码比较的电路，只要是简单的逻辑门电路就可以了，并不需要一个完整而复杂的ALU。

所以，我们可以将条件判断、地址跳转，都提前到指令译码阶段进行，而不需要放在指令执行阶段。对应的，我们也要在CPU里面设计对应的旁路，在指令译码阶段，就提供对应的判断比较的电路。

分支预测
最简单的分支预测技术，叫作“假装分支不发生”。顾名思义，自然就是仍然按照顺序，把指令往下执行。

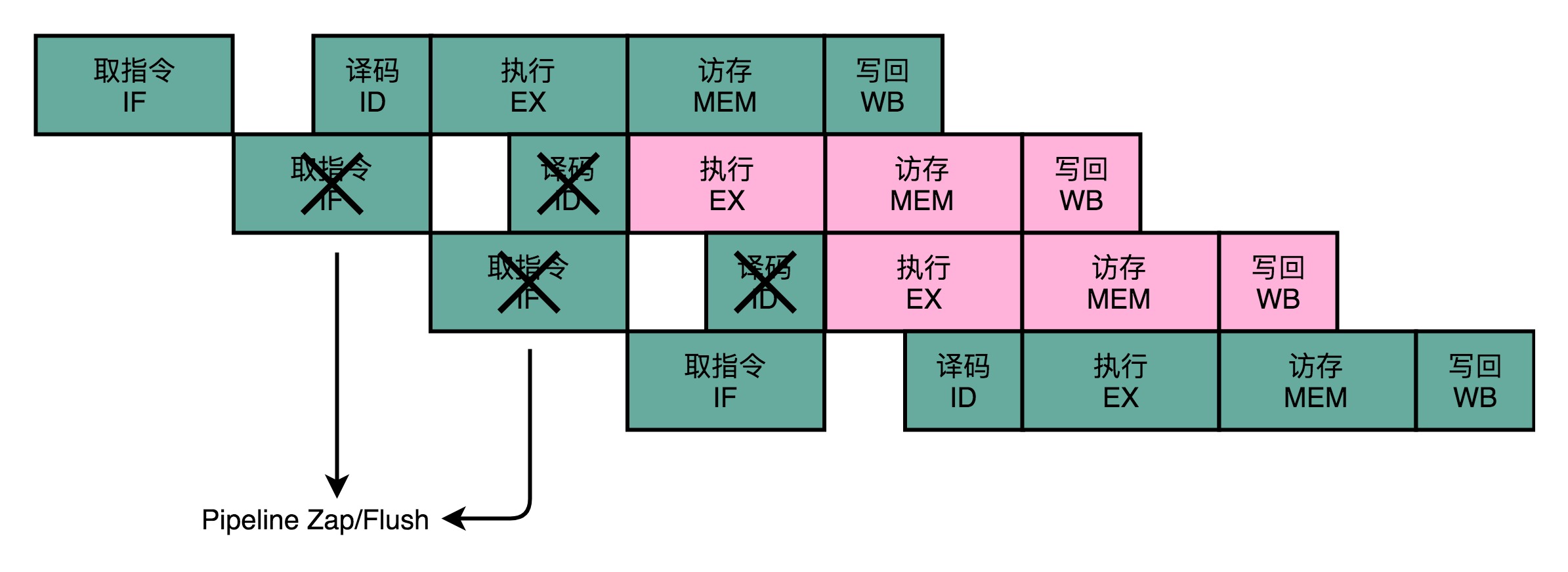
如果分支预测失败了呢？那我们就把后面已经取出指令已经执行的部分，给丢弃掉。这个丢弃的操作，在流水线里面，叫作Zap或者Flush。CPU不仅要执行后面的指令，对于这些已经在流水线里面执行到一半的指令，我们还需要做对应的清除操作。

动态分支预测
就是记录当前分支的比较情况，直接用当前分支的比较情况，来预测下一次分支时候的比较情况。

例子：

public class BranchPrediction {
    public static void main(String args[]) {        
        long start = System.currentTimeMillis();
        for (int i = 0; i < 100; i++) {
            for (int j = 0; j <1000; j ++) {
                for (int k = 0; k < 10000; k++) {
                }
            }
        }
        long end = System.currentTimeMillis();
        System.out.println("Time spent is " + (end - start));
                
        start = System.currentTimeMillis();
        for (int i = 0; i < 10000; i++) {
            for (int j = 0; j <1000; j ++) {
                for (int k = 0; k < 100; k++) {
                }
            }
        }
        end = System.currentTimeMillis();
        System.out.println("Time spent is " + (end - start) + "ms");
    }
}

输出：

Time spent in first loop is 5ms
Time spent in second loop is 15ms

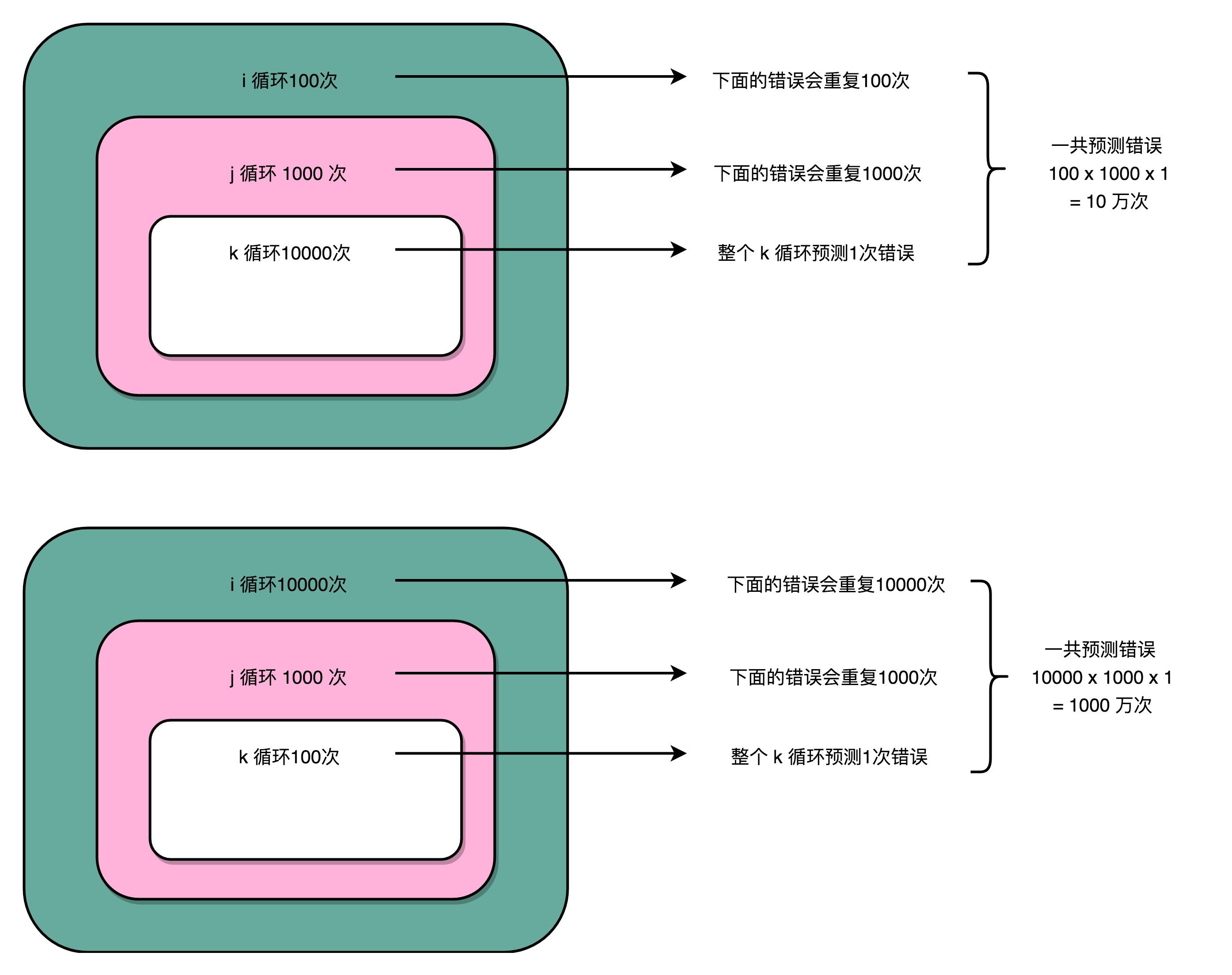
分支预测策略最简单的一个方式，自然是“假定分支不发生”。对应到上面的循环代码，就是循环始终会进行下去。在这样的情况下，上面的第一段循环，也就是内层 k 循环10000次的代码。每隔10000次，才会发生一次预测上的错误。而这样的错误，在第二层 j 的循环发生的次数，是1000次。

最外层的 i 的循环是100次。每个外层循环一次里面，都会发生1000次最内层 k 的循环的预测错误，所以一共会发生 100 × 1000 = 10万次预测错误。

操作数前推

通过流水线停顿可以解决资源竞争产生的问题，但是，插入过多的NOP操作，意味着我们的CPU总是在空转，干吃饭不干活。所以我们提出了操作数前推这样的解决方案。

add $t0, $s2,$s1
add $s2, $s1,$t0

第一条指令，把 s1 和 s2 寄存器里面的数据相加，存入到 t0 这个寄存器里面。
第二条指令，把 s1 和 t0 寄存器里面的数据相加，存入到 s2 这个寄存器里面。

我们要在第二条指令的译码阶段之后，插入对应的NOP指令，直到前一天指令的数据写回完成之后，才能继续执行。但是这样浪费了两个时钟周期。

这个时候完全可以在第一条指令的执行阶段完成之后，直接将结果数据传输给到下一条指令的ALU。然后，下一条指令不需要再插入两个NOP阶段，就可以继续正常走到执行阶段。

这样的解决方案，我们就叫作操作数前推（Operand Forwarding），或者操作数旁路（Operand Bypassing）。

CPU指令乱序执行

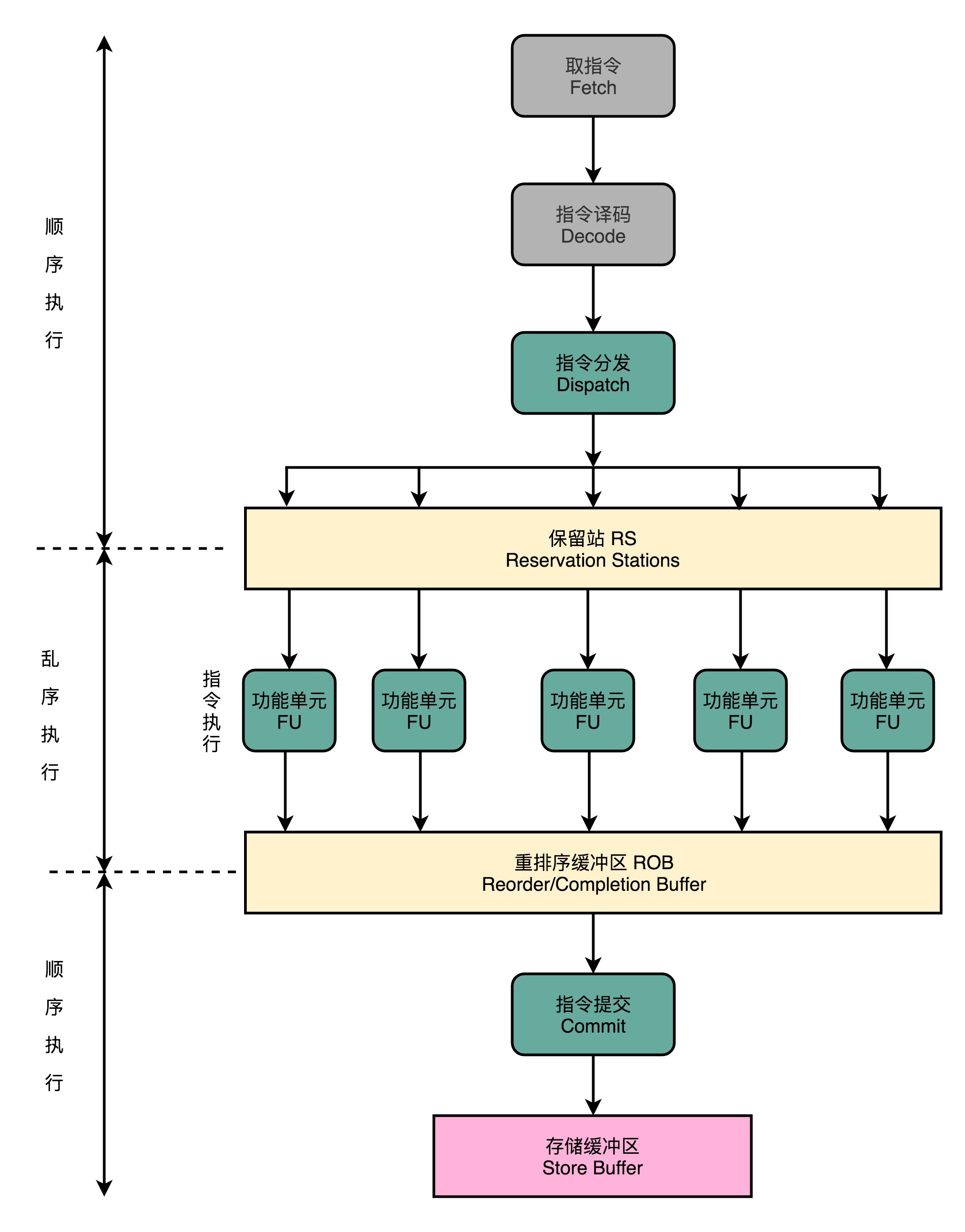
1. 在取指令和指令译码的时候，乱序执行的CPU和其他使用流水线架构的CPU是一样的。它会一级一级顺序地进行取指令和指令译码的工作。
2. 在指令译码完成之后，CPU不会直接进行指令执行，而是进行一次指令分发，把指令发到一个叫作保留站（Reservation Stations）的地方。
3. 这些指令不会立刻执行，而要等待它们所依赖的数据，传递给它们之后才会执行。
4. 一旦指令依赖的数据来齐了，指令就可以交到后面的功能单元（Function Unit，FU），其实就是ALU，去执行了。我们有很多功能单元可以并行运行，但是不同的功能单元能够支持执行的指令并不相同。
5. 指令执行的阶段完成之后，我们并不能立刻把结果写回到寄存器里面去，而是把结果再存放到一个叫作重排序缓冲区（Re-Order Buffer，ROB）的地方。
6. 在重排序缓冲区里，我们的CPU会按照取指令的顺序，对指令的计算结果重新排序。只有排在前面的指令都已经完成了，才会提交指令，完成整个指令的运算结果。
7. 实际的指令的计算结果数据，并不是直接写到内存或者高速缓存里，而是先写入存储缓冲区（Store Buffer面，最终才会写入到高速缓存和内存里。

在乱序执行的情况下，只有CPU内部指令的执行层面，可能是“乱序”的。

例子：

a = b + c
d = a * e
x = y * z

里面的 d 依赖于 a 的计算结果，不会在 a 的计算完成之前执行。但是我们的CPU并不会闲着，因为 x = y * z 的指令同样会被分发到保留站里。因为 x 所依赖的 y 和 z 的数据是准备好的， 这里的乘法运算不会等待计算 d，而会先去计算 x 的值。

如果我们只有一个FU能够计算乘法，那么这个FU并不会因为 d 要等待 a 的计算结果，而被闲置，而是会先被拿去计算 x。

在 x 计算完成之后，d 也等来了 a 的计算结果。这个时候，我们的FU就会去计算出 d 的结果。然后在重排序缓冲区里，把对应的计算结果的提交顺序，仍然设置成 a -> d -> x，而计算完成的顺序是 x -> a -> d。

在这整个过程中，整个计算乘法的FU都没有闲置，这也意味着我们的CPU的吞吐率最大化了。

乱序执行，极大地提高了CPU的运行效率。核心原因是，现代CPU的运行速度比访问主内存的速度要快很多。如果完全采用顺序执行的方式，很多时间都会浪费在前面指令等待获取内存数据的时间里。CPU不得不加入NOP操作进行空转。