链接: https://leetcode.com/problems/generate-parentheses/
【描述】
Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.
For example, given n = 3, a solution set is:
"((()))", "(()())", "(())()", "()(())", "()()()"
【中文描述】
给定一个数字n,要求写一个方法,生成所有n个括号的可能合法组合。
例如,n=3, 那么3个括号的所有可能组合如上。
————————————————————————————————————————————————————————————
【初始思路】
基本素养,只要见到求所有可能组合的情况(所有可能组合的个数), 首先立马想几个概念词:DFS、递归、回溯。有了这个直觉,你就省去了大量的时间,直接往递归上去套。接下来就是考虑怎么设计递归函数的问题了,速度自然会快很多。
这个题也是如此,回溯、递归。
怎么递归。
我开始的想法是,既然是合法组合,我干脆每次递归的时候直接选择一整个"()"组合作为递归添加项目就可以了。这样子不用考虑不合法的情况了。例如,要求2个括号的合法组合,那么先给一个括号,然后在这个括号的基础上,加第二个括号,无非有如下3种加法,我们用数字来表示可以填入第二个括号的位置:
0( 1 )2
也就是说,我们可以在0、1、2三个位置填入第二个括号,就能生成所有组合了。当然,填入2和填入0的效果是一样,后面讨论如何去重这种情况。
如果如题目要求,n=3时,那么可能的填入情况如下:
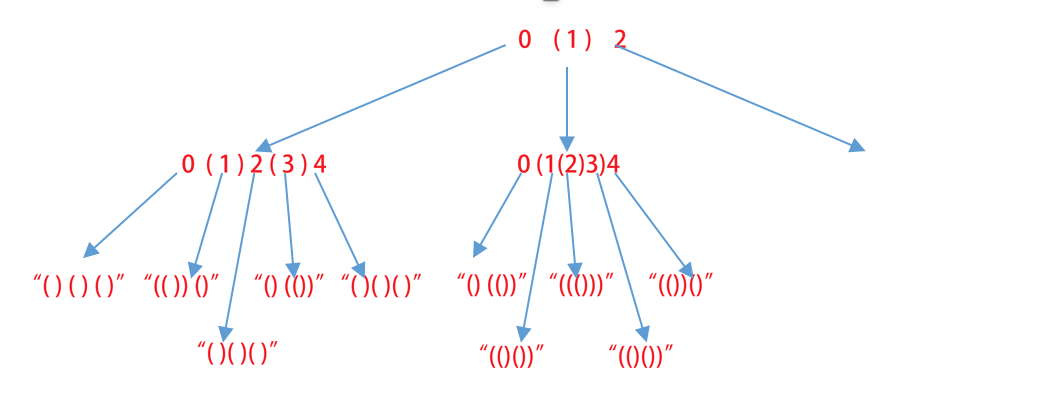
上图中,2衍生出来的那一支根本就不用再走,明显是重复的。所以没有画出其衍生的结果。
这其实是个树, 叶子就是所有我们能够生成的串的集合。每次生成可能的串后,检查下还需不需要加入括号,如果需要,继续递归进入下一层即可。如何控制基准条件?我们用一个int need来作为递归层数的控制(也即还需填入几个括号),当need=0的时候,显然当前串不需要再加入括号,直接返回一个空串给上层即可。如果need不为0,那么在生成当前串之后,在当前串基础上递归,need-1即可。
那么,如何实现在0,1,2,3,4这样的位置填入括号呢?我用了substring方法,每次传入一个当前串s,递归方法在当前串的基础上动手脚,要把当前的括号加入0的位置,其实就是拿一个stringbuilder,先appen当前括号,然后再append(s(0位置后))。如果要在1的位置加括号,就是sb.append(s(0,1)), 再append当前括号,然后再append(s剩余串)。我们用一个for循环来实现这个功能,循环次数就是当前传入串s的长度。
那么好了,讨论到这里,不去重的代码就可以写出来了。那么,如何去重呢?
我们看上面的串,所有中间结果都会衍生出一个后续的结果。如果中间结果和之前已经生成过的串一样,那肯定不用往下走了,再走也是重复。基于这个思路,我用了一个HashMap,存入所有中间结果串,每次生成中间串的时候,在map里找找看,如果已经生成过这个串,直接continue考虑下一种可能性。如果没有,那么当前串入map,接着递归继续衍生。
好了,代码如下。
【Show me the Code!!!】

1 /** 2 * 主驱动程序 3 * @param n 4 * @return 5 */ 6 public static List<String> generateParenthesis(int n) { 7 List<String> list = new ArrayList<String>(); 8 if(n == 0) { 9 list.add(new String("")); 10 return list; 11 } 12 Map<String, Integer> map = new HashMap<String, Integer>(); //用于记录已经出现过的串 13 return recursiveGenerator("", map, n); 14 } 15 16 /** 17 * 递归主方法 18 * 在已有串: para中找出各个位置, 分别插入(),并形成list返回 19 * @param para 已有串 20 * @param need 还需几个(), need==1时为基准条件 21 * @return 22 */ 23 public static List<String> recursiveGenerator(String para, Map<String, Integer> map, int need) { 24 if (need == 0) { 25 //base condition 26 return new ArrayList<String>(); 27 } else { 28 //non base condition 29 //在para中找各个位置,加入一个(),然后直接返回 30 List<String> list = new ArrayList<String>(); 31 for (int i = 0; i <= para.length(); i++) { 32 StringBuilder sb = new StringBuilder(); 33 sb.append(para.substring(0,i)) 34 .append("()").append(para.substring(i, para.length())); 35 //子结果去重 36 if(map.containsKey(sb.toString())) {continue;} 37 else { 38 map.put(sb.toString(), 1); 39 } 40 List<String> rec = recursiveGenerator(sb.toString(), map, need - 1); 41 if(rec.size() == 0) { 42 list.add(sb.toString()); 43 } else { 44 for(String s : rec) { 45 list.add(s); 46 } 47 } 48 } 49 return list; 50 } 51 }
可是这个代码还是笨,首先用了HashMap,耗空间不说,速度也可能会受到一定影响。果然,运行了一下, 8个用例跑了13ms。有没有更快的办法?
【重整思路】
换个角度考虑问题,我上面是把左右括号作为一个整体做考虑,然后插入的。我们能不能把左右括号拆开,从左往右写,看看能写出多少可能性?这其实是人类正常的思维方式。由于要写出所有的合法括号组合,先写左括号,左括号全部用完,再写右括号,这将是第一个最容易想到的可能性。然后呢?肯定需要回溯了。回溯到一个位置,我们不写"(",写一个")"然后再试着写写看。如此往复,所有的可能就全部写出来。此外,这个方法还完美解决了重复情况的可能性。因为每一次新的尝试,都是"新"的尝试,之前从来没有尝试过,所以不可能产生已经出现过的结果。具体可以看下面图帮助理解:

上图可以清楚的看到n=3的时候,这种递归方案的全部过程,从左到右递归,直到紫色回溯的时候,再也找不到其他方案,最终回到最初,全部流程结束。
具体实现,有几个核心的点需要注意。如何实现优先选择写"("? 如何控制回溯? 其实答案就隐含在上面的图片里。
虚线箭头其实就是程序走到最终情况时候,往回一路返回的过程。没返回一次,程序需要检查一下是否还有其他合法情况,如果没有继续返回。直到找到合法情况,进入下一个合法情况。
如何检查是否还有合法情况?很简单,合法括号的含义就是有几个左括号,就必然要对应给几个右括号。那么每一次返回之后,看看是否还有"("可以用,如果有,就用一个左括号,然后进入该情况递归。如果没有,就继续返回。所以,我们需要一个左括号计数器来判断是否还有可以用的左括号。那么如何判断走到最终结果了呢?对了!右括号计数器。当右括号和左括号同时用完的时候,我们就认为走到最终结果了,直接return。
到这里就可以了么?如上图,紫色最终回溯到起点第一个左括号之后,按道理还可以继续回溯,然后第一个字符直接填入一个")", 结果岂不是就错了。而这种情况是显而易见会发生的。这其实就给我们了一个教训,递归方法不是只需要关注基准条件就可以的,还需要考虑某种情况下是否不合法!这个题就是最好的例子。按照通用逻辑,左括号先写的情况全部试过后,就得试右括号先写的情况了,这种情况下明显是不合法的。处理方法也很简单。每次递归的时候先检查一下剩余的右括号是否小于左括号,如果是的话,说明先写了右括号,不合法直接返回。
最后,代码就可以写出来了。
【Show me the Code!!!】

1 public class OtherSolution { 2 /** 3 * 定义全局变量,无需再传值到各个方法 4 */ 5 static List<String> list = new ArrayList<String>(); 6 7 public static List<String> generateParenthesis(int n) { 8 /** 9 * 初始状态,左括号和右括号都可以添加n个,所以左右都传了n 10 */ 11 generateLeftsAndRights("",n,n); 12 return list; 13 } 14 15 /** 16 * DFS方法 17 * 该方法的本质是,每次调用都深度优先用掉左括号,然后再用掉右括号. 18 * @param subList 记录每次递归时候当前串, 方法将在subList上继续添加括号 19 * @param left 左括号还剩下的个数 20 * @param right 右括号还剩下的个数 21 */ 22 private static void generateLeftsAndRights(String subList,int left, int right){ 23 /** 24 * 最后可能出现的情况, 右括号比左括号先用完, 明显不是合法的串,应剔除 25 */ 26 if(left > right) return; 27 28 /** 29 * 左括号还剩得有, 优先用左括号 30 * 该方法将不断深搜, 直到左括号全部用完 31 */ 32 if(left > 0){ 33 generateLeftsAndRights(subList + "(", left-1, right); 34 } 35 36 /** 37 * 开始用右括号 38 */ 39 if(right > 0){ 40 generateLeftsAndRights(subList + ")", left, right-1); 41 } 42 43 /** 44 * 基准情况, 各自都用完, 说明已经形成了一个合法的串,将该串加入list返回 45 */ 46 if(left == 0 && right == 0){ 47 list.add(subList); 48 return; 49 } 50 } 51 }
最后,重申,凡是遇到要求全部可能集合、可能性、可能性个数的题目,立马考虑递归回溯求解!!!
