伸展树同样是一种平衡二叉搜索树,它的优势在于,在足够长的序列中能保证分摊意义上的高效率,同时也无需记录高度或者平衡因子等信息。
伸展树的高效前提是局部性:刚刚被访问到的数据,可能在短时间内被再次访问;将被访问的下一元素,可能就在不久之前刚刚访问过的元素的附近。因此,伸展树的策略,就是把刚刚访问到的节点,及时“伸展”到树根附近。
所谓“伸展”操作,其实就是BST中的旋转操作。如果每次经过适当旋转,将访问的节点提升一层,直到上升到树根,称为逐层伸展。可以验证,这种伸展方式可能会是低效的,而且会导致结构复原,因此,使用双层伸展代替。
顾名思义,双层伸展就是每次将当前节点v上升两层。根据当前节点v与父亲节点p和祖父g的关系,可以分为三类:
(1)v p g同侧的时候,此时进行zig-zig或者zag-zag即可。
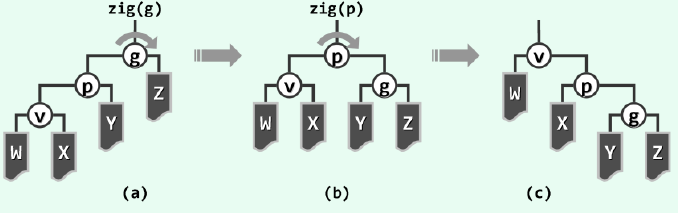
(2)v p g不同侧的时候,此时进行zig-zag或者zag-zig即可。
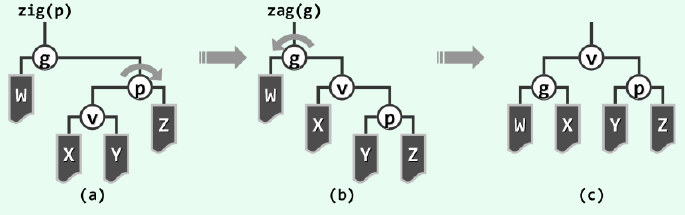
(3)当v的祖父g已经不存在,即v需要上升的层数为奇数时,只需要简单的zig/zag即可。
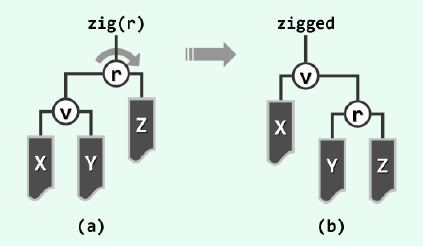
伸展树的代码实现:
1 #include"BST.h" 2 template<typename T> class Splay :public BST<T> 3 { 4 protected: 5 BinNodePosi(T) splay(BinNodePosi(T) v);//将节点v伸展至根 6 public: 7 BinNodePosi(T)& search(const T& e) override;//查找 8 BinNodePosi(T) insert(const T& e) override; 9 bool remove(const T& e) override; 10 };
1 template<typename T> BinNodePosi(T) Splay<T>::splay(BinNodePosi(T) v) 2 { 3 if (!v) return NULL; BinNodePosi(T) p; BinNodePosi(T) g; 4 while ((p = v->parent) && (g = p->parent)) 5 { 6 BinNodePosi(T) gg = g->parent;//每轮之后以原曾祖父为父亲 7 if(IsLChild(*v)) 8 if (IsLChild(*p)) //zig-zig 9 { 10 attachAsLChild(g, p->rc); attachAsLChild(p, v->rc); 11 attachAsRChild(p, g); attachAsRChild(v, p); 12 } 13 else//zig-zag 14 { 15 attachAsLChild(p, v->rc); attachAsRChild(g, v->lc); 16 attachAsLChild(v, g); attachAsRChild(v, p); 17 } 18 else if (IsLChild(*p)) 19 { 20 attachAsRChild(g, p->lc); attachAsLChild(p, v->rc); 21 attachAsRChild(p, g); attachAsLChild(v, p); 22 } 23 else 24 { 25 attachAsRChild(p, v->lc); attachAsLChild(g, v->rc); 26 attachAsRChild(v, g); attachAsLChild(v, p); 27 } 28 if (!gg) v->parent = NULL;//不存在曾祖父,v已经是树根 29 else//否则,根据g是左子树还是右子树,连接曾祖父和v 30 (g == gg->lc) ? attachAsLChild(gg, v) : attachAsRChild(gg, v); 31 updateHegiht(g); updateHeight(p); updateHegiht(v); 32 } 33 if (p = v->parent)//如果v还存在父亲,做一次单旋 34 { 35 if (IsLChild(*v)) { attachAsLChild(p, v->rc); attachAsRChild(v, p); } 36 else { attachAsRChild(p, v->lc); attachAsLChild(v, p); } 37 updateHegiht(p); updateHegiht(v); 38 } 39 v->parent = NULL; return v;//此时v必然已经是树根了 40 }
可以看到,双旋的部分分为4种位置情况,之后再判断是否需要进行一次单旋,最后返回旋转到树根位置的v节点。
1 template<typename T> BinNodePosi(T)& Splay<T>::search(const T& e) 2 { 3 BinNodePosi(T) p = searchIn(_root, e, _hot = NULL); 4 _root = spaly(p ? p : _hot);//将最后一个被访问者延伸到树根 5 return _root;//_root指向最后被访问的节点,要么是查找目标,要么是_hot 6 }
查找操作,主体就是查找后进行伸展操作。
1 template<typename T> BinNodePosi(T) Splay<T>::insert(const T&e) 2 { 3 if (!_root) { _size++; return _root = new BinNode<T>(e); } 4 if (e == search(e)->data) return _root; 5 _size++; 6 BinNodePosi(T) t = _root;//创建新节点 7 if (_root->data < e)//新插入节点大于原根,以t和t->rc作为孩子 8 { 9 t->parent = _root = new BinNode<T>(e, NULL, t, t->rc);//插入新节点以及设置父子 10 if (HasRChild(*t)) { t->rc->parent = _root; t->rc = NULL; }//原根的右子树接入新节点 11 } 12 else//...小于原根,把原根节点作为右孩子 13 { 14 t->parent = _root = new BinNode<T>(e, NULL, t->lc, t); 15 if (HasLChild(*t)) { t->lc->parent = _root; t->lc = NULL; } 16 } 17 return _root;//返回树根,也就是新插入的节点 18 }
插入操作,首先进行查找,判断是否已经存在,并且把查找的结果伸展到树根。再根据根节点与插入的节点大小关系,最终把插入的节点设置为树根。
1 template<typename T> bool Splay<T>::remove(const T& e)//删除节点,将原节点的父亲升至树根 2 { 3 if (!_root || (e != search(e)->data)) return false;//失败时直接返回 4 BinNodePosi(T) w = _root; 5 if (!HasLChild(*_root))//如果没有左子树 6 { 7 _root = _root->rc; 8 if (_root) _root->parent = NULL; 9 } 10 else if (!HasRChild(*_root))//没有右子树 11 { 12 _root = _root->lc; 13 if (_root) _root->parent = NULL; 14 } 15 else //左右子树都存在 16 { 17 BinNodePosi(T) lTree = _root->lc;//记录左子树 18 lTree->parent = NULL;//分离左子树 19 _root->lc = NULL; 20 _root = _root->rc; _root->parent = NULL;////保留右子树 21 search(w->data);//必定失败,但是能把后继(右子树中最小的节点)升至根 22 _root->lc = lTree; lTree->parent = _root;//接入原左子树 23 } 24 _size--; 25 if(_root) updateHeight(_root); 26 return true; 27 }
删除操作,把被删除节点的父亲升为树根。具体地,如果两个子树有一个不存在,只需要改为左右孩子然后释放原树根节点。如果两个孩子均存在,就需要寻找后继,并升到树根位置。
最后,分析一下伸展树的优缺点。伸展树的优点,在于分摊效率高,单次操作在O(logn)时间内完成,且对于局部利用率高的情况效率高。缺点也很明显,就是树的结构变化非常大,而且最坏情况下,单次操作最好也需要n的时间。