在计算机图形学中,网格是一种非常基本的表示方法。随着近些年三维表面重建和Dense SLAM的兴起,从海量的三维点云数据生成单一的网格的方法得到了大量的应用。特别是在AR中,因为交互的需要,网格生成算法经常是一个必选项。
由于工作中正好涉及到一些这方面的应用,因此想简单介绍一下这方面的知识。以下仅讨论三维情形。
本文很多内容来源于Matthew Bolitho的博士论文[1]。这位仁兄现在在NVidia做Director of Architecture。
算法的输入输出
网格生成算法的输入一般为三维点云,输出为三维网格。输入的点云一般为若干个点云的集合。输出的网格一般为单一的网格。
输入的点云一般有如下几种形式:
- 只包含三维坐标的点云
(P={p_1,...,p_N})
- 包含三维坐标和法向量的点云
(P={(p_1,n_1),...,(p_n,n_N)})
- 深度图
2D 网格(Rinmathbf{R}^{N imes M}),实际上包含了三维坐标,表面法向量和邻域信息。
输入的点云一般面临着下面几个问题,如下图所示:

- 点云噪声
每个点云都会带有噪声,噪声有可能和物体表面光学性质、物体深度、传感器性能等都有关系。
- 点云匹配误差
三维重建中需要将不同帧得到的点云估计其在世界坐标系下的位姿,会引入一定的位置误差。
- 点云分布
分布的不均匀性体现在(1)每个小点云在不同的方向上分布是不均匀的(虽然传感器上看是均匀的)如上图3位置,(2)不同的点云匹配在一起时,不同位置的点云密度是不一样的,如上图2位置。
- 缺失数据
扫描中如果碰到不易成像的部位(比如不可见、反光等等),那么这部分的数据是缺失的,即点云是不完整的。如上图1位置所示。
对算法的要求
一般而言,我们对于输出的网格有一定的要求。除了网格密度和精度以外,我们还希望算法
- 对点云噪声有一定的冗余度。
- 能够重建出曲率变化比较大的曲面。
- 能够处理大数据量,算法时间和空间复杂度不会太高。
- 重建出的网格中包含尽可能少的异常三角片,比如三角片交错在一起、表面法向量不连续或不一致、同一个位置附近出现多层三角片等。
这些要求也构成了算法的难点。
一般方法
网格生成算法可以分为离散方法和连续方法两大类。离散方法利用某些空间划分方法,直接从点云数据生成网格。连续方法利用点云去拟合某类分布函数,得到表面的函数表示,然后生成网格。总结见下图。
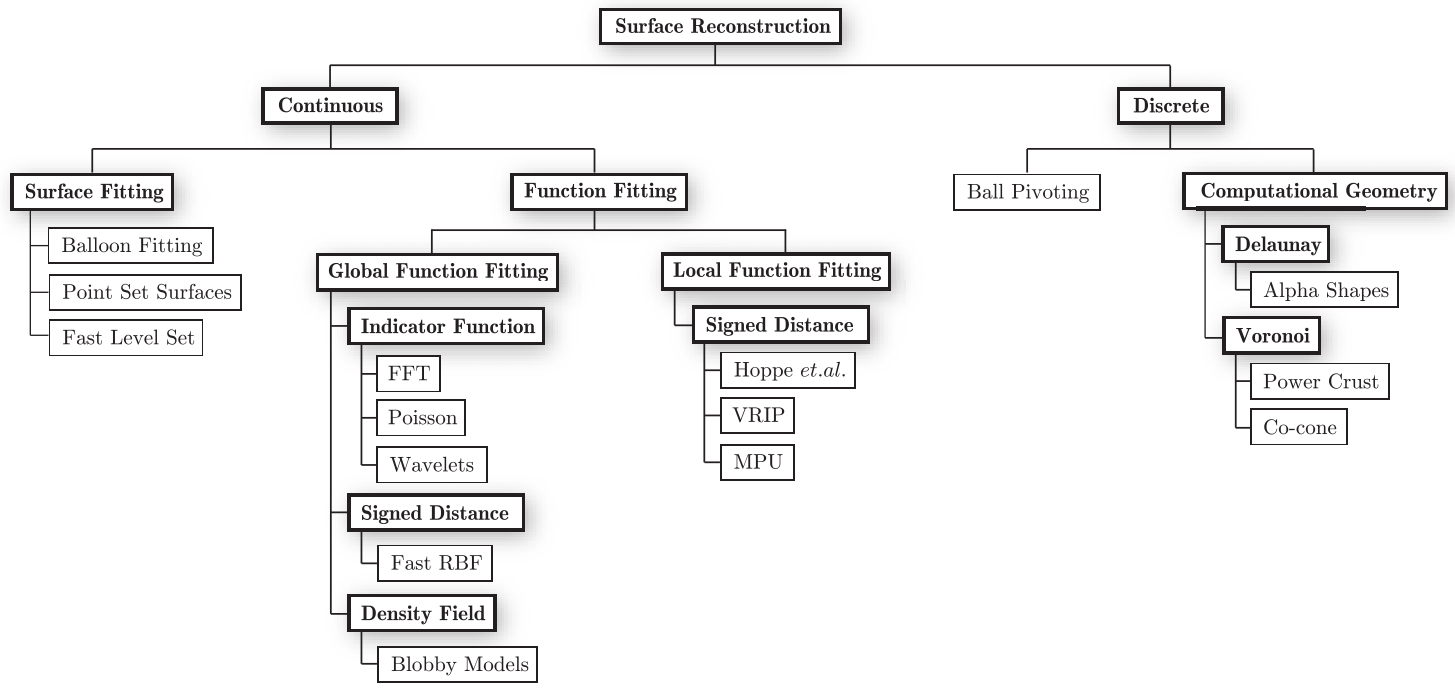
下面简单介绍一下两种重建思想,都是基于连续方法的。
有符号距离函数(signed distance function)
定义(S)是待重建的曲面,(F:mathbf{R}^3->mathbf{R}),其中(F(x))定义为(x)到(S)中的距离最近的点的距离。如果(x)在(S)外面,则距离为正,反之为负。那么,
(S={x:F(x)=0})
典型的方法有VRIP(Volumetric Range Image Processing)。下图是实际应用中通过VRIP生成的(F(x))的一个切面。
图中(F(x))的值被灰度取代后,实际上(S={x:F(x)=128})

指示函数(indicator function)
对于一个给定的物体(M),定义指示函数
(chi_M(x)=1 ext{ if } xin M ext{ and } chi_M(x)=0 ext{ if }x
otin M)
那么(S=partial M)。
因此把重构(S)的问题转换为重构(chi_M)的问题。而利用Stokes公式,可以将点云及其法向量((chi_M)的表面信息)和(chi_M)联系起来。
典型的方法是FFT重建和Poisson重建。下图是Poisson重建方法的原理图。
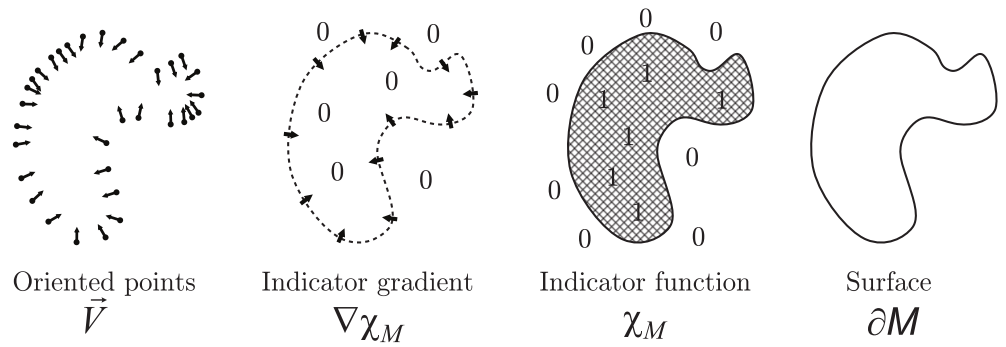
后续会分别介绍一下VRIP和Poisson,以及他们在SLAM中的应用。