之前写过一个随笔,描述怎么用 gnuplot 绘制球谐函数图:https://www.cnblogs.com/luyi07/p/14713231.html
其中提到,在画球谐函数这事上,python的缺点是图片不能旋转,图片小不够清楚华丽,代码细节多(其实也还好,多一点点)。
现在,真香定律显现,我发现,python的上述缺点确实存在,但是,gnuplot没有内置的球谐函数,得自己写,而我,懒得写了,所以还是(真香!)用python画吧,等有空了再自己写一个gnuplot内置的球谐函数,然后用pm3d画吧,gnuplot渲染得确实更好看。
1. 球谐函数定义
不同的书上有不同的约定,咱还是用 Condon-Shortley 相位约定,定义如下:
[Y^m_n( heta,phi) equiv (-1)^m sqrt{ frac{2n+1}{4pi} frac{(n-m)!}{(n+m)!} } P^m_n(cos heta) e^{imphi},
]
其中,((-1)^m)即Condon-Shortley相因子,大概是为了方便做角动量代数的,连带勒让德函数定义为(Rodriguez公式):
[P^m_n(x) equiv frac{1}{2^n n!} (1-x^2)^{m/2} frac{ d^{n+m} }{ d x^{n+m} } (x^2-1)^n.
]
这里球谐函数的定义与上一个帖子(https://www.cnblogs.com/luyi07/p/14713231.html)是一致的,但是连带勒让德函数的定义略有不同。
2. 球谐函数的绘制代码
import numpy as np
import matplotlib.pyplot as plt
from scipy import special
import mpl_toolkits.mplot3d.axes3d as axes3d
theta, phi = np.linspace(0, np.pi, 100), np.linspace(0, 2*np.pi, 100)
THETA, PHI = np.meshgrid(theta, phi)
#help(special.sph_harm)
R = (special.sph_harm(2,3,PHI,THETA).real)**2
X = R * np.sin(THETA) * np.cos(PHI)
Y = R * np.sin(THETA) * np.sin(PHI)
Z = R * np.cos(THETA)
fig = plt.figure()
ax = fig.add_subplot(1,1,1, projection='3d')
plot = ax.plot_surface(
X, Y, Z, rstride=1, cstride=1, cmap=plt.get_cmap('jet'),
linewidth=0, antialiased=False, alpha=0.5)
# below are codes copied from stackoverflow, to make the scaling correct
max_range = np.array([X.max()-X.min(), Y.max()-Y.min(), Z.max()-Z.min()]).max() / 2.0
mid_x = (X.max()+X.min()) * 0.5
mid_y = (Y.max()+Y.min()) * 0.5
mid_z = (Z.max()+Z.min()) * 0.5
ax.set_xlim(mid_x - max_range, mid_x + max_range)
ax.set_ylim(mid_y - max_range, mid_y + max_range)
ax.set_zlim(mid_z - max_range, mid_z + max_range)
#ax.view_init(elev=30,azim=0) #调节视角,elev指向上(z方向)旋转的角度,azim指xy平面内旋转的角度
plt.show()
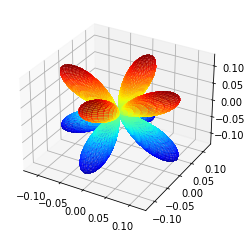
效果如上图所示。说明以下几点:
- plt.show() 上面的那一行,ax.view_init(...)可以调节观看者的视角
- 再往上一大段代码,是为了保证 xyz三个方向的坐标比例完全相同
- 再往上才是画图的核心代码,即在立体角各个角度取点,然后使用 plot_surface 函数绘制,其中有染色方案的参数,这部分代码是从网上找来以后自己改的。
- 如果需要保存图片,可以添加一行 plt.savefig("xx.jpg"),应该就行了。
综上所述,我在网上分别找了 plot_surface用法,球谐函数调用,scaling方案,视角变换,然后结合两本教材上球谐函数的相位约定(教材见下面),花了1个多小时实践操作总结,得到了这篇博客。亲爱的读者,它就这样来到你的面前。
3. 鸣谢
- D. J. Griffiths, "Introduction to Quantum Mechanics",及郑州大学中文译本
- Arfken, Weber, "Mathmatical Methods for Physicists"