引入
Problem
现在有一个无根树,要你确定一个根,使得其他点到这个根的距离最短。(n le 10^5)
Solution
Thinking 1
枚举根,dfs暴力求距离,取最大值,时间复杂度(mathcal{O}(n^2))。
Thinking 2
如果让根的子树变成根,那个树的形态其实很多都没变!如果再来一次(mathcal{O}(n))的话,太浪费了!
我们考虑先选一个根节点(默认为1),然后dfs子树来更新。
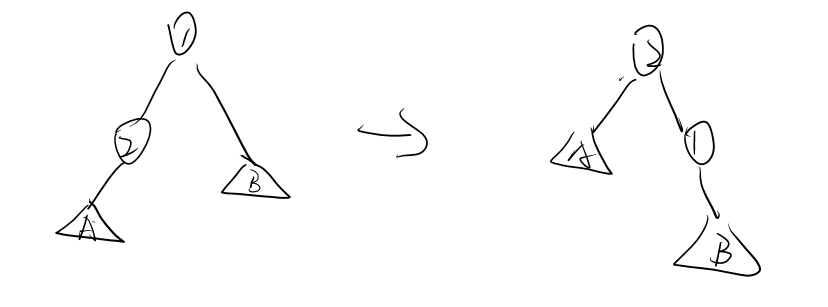
假设我们现在已经通过第一次dfs算出了(dp[1])(以1为根的答案),来求(dp[2])。不难发现,(2)和(A)的深度都相比一开始减1,那么对答案的贡献就是减子树的大小,即(siz[2]),然后除了(2)和(A)以外的所有点深度都加1,对答案的贡献加(n - siz[2])。
整理得
[dp[2] = dp[1] - siz[2] + n - siz[2] = dp[1] + n - 2siz[2]
]
推广到一般形式:
[dp[v] = dp[x] + n - 2siz[v]
]
不难发现只需要两次dfs,所以时间复杂度为(mathcal{O}(n))。
做法
1.先定一个根(一般是1),然后先算出答案,同时预处理一些转移需要的东西。
2.根据具体题目推式子转移。