Codeforces Round #236 (Div. 2)

A. Nuts

time limit per test：1 second
memory limit per test:256 megabytes
input:standard input
output:standard output

You have a nuts and lots of boxes. The boxes have a wonderful feature: if you put x (x ≥ 0) divisors (the spacial bars that can divide a box) to it, you get a box, divided into x + 1 sections.

You are minimalist. Therefore, on the one hand, you are against dividing some box into more than k sections. On the other hand, you are against putting more than v nuts into some section of the box. What is the minimum number of boxes you have to use if you want to put all the nuts in boxes, and you have b divisors?

Please note that you need to minimize the number of used boxes, not sections. You do not have to minimize the number of used divisors.

Input

The first line contains four space-separated integers k, a, b, v (2 ≤ k ≤ 1000; 1 ≤ a, b, v ≤ 1000) — the maximum number of sections in the box, the number of nuts, the number of divisors and the capacity of each section of the box.

Output

Print a single integer — the answer to the problem.

Sample test(s)

input

3 10 3 3

output

2

input

3 10 1 3

output

3

input

100 100 1 1000

output

1

Note

In the first sample you can act like this:

• Put two divisors to the first box. Now the first box has three sections and we can put three nuts into each section. Overall, the first box will have nine nuts.
• Do not put any divisors into the second box. Thus, the second box has one section for the last nut.

In the end we've put all the ten nuts into boxes.

The second sample is different as we have exactly one divisor and we put it to the first box. The next two boxes will have one section each.

题意：给你四个数字，k，a，b，v，分别代表着一个盒子最大的section，nut的数量，板的数量，每个section能容纳的最多的nut的数量。让你求出最少可以用几个盒子来装

思路：这个比赛的时候想复杂了，结果就悲剧了。。。。。我分了好多种情况，实际上我分的那些情况如果真拿出来的话能写成很多不同的方法A了这道题T_T。。。。。主要注意一下别让nut的数量小于0还有挡板的数量也要注意

#include <iostream>
#include <stdio.h>

using namespace std;

int main()
{
    int k ,a,b,v ;
    while(~scanf("%d %d %d %d",&k,&a,&b,&v))
    {
        int ans = 0 ;
        int temp = (a-1)/v+1 ;
        while(a > 0)
        {
            b++ ;
            for(int i = 1 ; i <= k && b ; i++)
            {
                a -= v ;
                b -= 1 ;
            }
            ans++ ;
        }
        printf("%d
",ans) ;
    }
    return 0;
}

#include<stdio.h>

int main()
{
    int k,a,b,v;
    scanf("%d %d %d %d",&k,&a,&b,&v);
    int temp = (a-1)/v+1;//求出放下所有的nut需要多少section
    printf("%d
",max((temp-1)/k+1,temp-b));//因为结果受制于板的数量和盒子所能容纳的section的数量
    return 0;
}

B. Trees in a Row

time limit per test： 1 second

                                                                                             memory limit per test：

256 megabytes

input ：

standard input

output：

standard output

The Queen of England has n trees growing in a row in her garden. At that, the i-th (1 ≤ i ≤ n) tree from the left has height ai meters. Today the Queen decided to update the scenery of her garden. She wants the trees' heights to meet the condition: for all i (1 ≤ i < n),ai + 1 - ai = k, where k is the number the Queen chose.

Unfortunately, the royal gardener is not a machine and he cannot fulfill the desire of the Queen instantly! In one minute, the gardener can either decrease the height of a tree to any positive integer height or increase the height of a tree to any positive integer height. How should the royal gardener act to fulfill a whim of Her Majesty in the minimum number of minutes?

Input

The first line contains two space-separated integers: n, k (1 ≤ n, k ≤ 1000). The second line contains n space-separated integersa1, a2, ..., an (1 ≤ ai ≤ 1000) — the heights of the trees in the row.

Output

In the first line print a single integer p — the minimum number of minutes the gardener needs. In the next p lines print the description of his actions.

If the gardener needs to increase the height of the j-th (1 ≤ j ≤ n) tree from the left by x (x ≥ 1) meters, then print in the corresponding line "+ j x". If the gardener needs to decrease the height of the j-th (1 ≤ j ≤ n) tree from the left by x (x ≥ 1) meters, print on the corresponding line "- j x".

If there are multiple ways to make a row of trees beautiful in the minimum number of actions, you are allowed to print any of them.

Sample test(s)

input

4 1
1 2 1 5

output

2
+ 3 2
- 4 1

input

4 1
1 2 3 4

output

0

题意 ：n棵树，希望后一棵树比前一棵树高k米，一次可以将一棵树加高若干米或减少若干米，问你最少需要修剪几棵树，然后将具体修剪输出

思路 ：这个题比赛的是愣是没反应过来，看了大神的代码才知道思路 ，就是说先找出以谁为基准让别的改变，给出k就可以求每个相对于第一个的增量求出来，然后用自身减这个增量，哈希一下，出现次数最多的那个数就是可以作为基准的，即第一个数，说不清楚，，，，，，

#include <stdio.h>
#include <string.h>
#include <iostream>

using namespace std ;

int a[1001],b[1001001] ;
int main()
{
    int n,k ;

    while(~scanf("%d %d",&n,&k))
    {
        int j = 1 ;
        memset(b,0,sizeof(b)) ;
        memset(a,0,sizeof(a)) ;
        for(int i = 0 ; i < n ; i++)
        {
            scanf("%d",&a[i]) ;
            if(a[i]-i*k > 0)
                b[a[i]-i*k]++ ;
        }
        for(int i = 0 ; i < 1001000 ; i++)
            if(b[i] > b[j]) j = i ;
        printf("%d
",n-b[j]) ;
        for(int i = 0 ; i < n ; i++)
        {
            if(j != a[i])
            {
                if(j > a[i])
                    printf("+ %d %d
",i+1,j-a[i]) ;
                else if(j < a[i])
                    printf("- %d %d
",i+1,a[i]-j) ;
            }
            j += k ;
        }
    }
    return 0 ;
}

C. Searching for Graph

time limit per test：1 second
memory limit per test：256 megabytes
input：standard input
output：standard output

Let's call an undirected graph of n vertices p-interesting, if the following conditions fulfill:

• the graph contains exactly 2n + p edges;
• the graph doesn't contain self-loops and multiple edges;
• for any integer k (1 ≤ k ≤ n), any subgraph consisting of k vertices contains at most 2k + p edges.

A subgraph of a graph is some set of the graph vertices and some set of the graph edges. At that, the set of edges must meet the condition: both ends of each edge from the set must belong to the chosen set of vertices.

Your task is to find a p-interesting graph consisting of n vertices.

Input

The first line contains a single integer t (1 ≤ t ≤ 5) — the number of tests in the input. Next t lines each contains two space-separated integers: n, p (5 ≤ n ≤ 24; p ≥ 0; 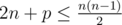) — the number of vertices in the graph and the interest value for the appropriate test.

It is guaranteed that the required graph exists.

Output

For each of the t tests print 2n + p lines containing the description of the edges of a p-interesting graph: the i-th line must contain two space-separated integers ai, bi (1 ≤ ai, bi ≤ n; ai ≠ bi) — two vertices, connected by an edge in the resulting graph. Consider the graph vertices numbered with integers from 1 to n.

Print the answers to the tests in the order the tests occur in the input. If there are multiple solutions, you can print any of them.

Sample test(s)

input

1
6 0

output

1 2
1 3
1 4
1 5
1 6
2 3
2 4
2 5
2 6
3 4
3 5
3 6

题意 ：给你n和p，让你构造一个图，满足3个条件，1是这个图刚好有2*n+p条边，2是没有环和重边，3是该图的任何一个只有K个顶点的子图，最多有2*k+p条边

思路 ：CF刷人玩儿呢，这么道大水题放在C题，害我只纠结AB了，早知道我先去把C做了，这个分数啊，其实就是按样例那样敲就行了。。。。。

#include <stdio.h>
int main()
{
    int T ;
    int n, p;
    scanf("%d",&T) ;
    while(T--)
    {
        scanf("%d %d",&n,&p) ;
        int cnt = 0 ;
        for(int i = 1 ; i <= n ; i++)
        {
            if(cnt == 2*n+p)
                break ;
            for(int j = i+1 ; j <= n ; j++)
            {

                printf("%d %d
",i,j) ;
                cnt++ ;
                if(cnt == 2*n+p)
                    break ;
            }
        }
    }
    return 0 ;
}