Codeforces Round #272 (Div. 1) A. Dreamoon and Sums（数论）

题目链接

Dreamoon loves summing up something for no reason. One day he obtains two integers a and b occasionally. He wants to calculate the sum of all nice integers. Positive integer x is called nice if 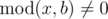 and 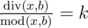, where k is some integer number in range[1, a].

By 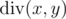 we denote the quotient of integer division of x and y. By  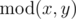we denote the remainder of integer division of x andy. You can read more about these operations here: http://goo.gl/AcsXhT.

The answer may be large, so please print its remainder modulo 1 000 000 007 (10⁹ + 7). Can you compute it faster than Dreamoon?

Input

The single line of the input contains two integers a, b (1 ≤ a, b ≤ 10⁷).

Output

Print a single integer representing the answer modulo 1 000 000 007 (10⁹ + 7).

题意 ： 给你a，b。让你找出符合以下条件的x，div(x,b)/mod(x,b)=k，其中k所在范围是[1,a]，其中mod(x,b)!= 0.然后将所有符合条件的x加和，求最后的结果

官方题解 ：

If we fix the value of k, and let d = div(x, b), m = mod(x, b), we have :
d = mk
x = db + m
So we have x = mkb + m = (kb + 1) * m.
And we know m would be in range [0, b - 1] because it's a remainder, so the sum of x of that fixed k would be .
Next we should notice that if an integer x is nice it can only be nice for a single particular k because a given x uniquely definesdiv(x, b) and mod(x, b).
Thus the final answer would be sum up for all individual k: 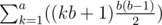 which can be calculated in O(a) and will pass the time limit of 1.5 seconds.
Also the formula above can be expanded to .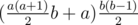 

#include <stdio.h>
#include <string.h>
#include <iostream>

using namespace std ;
#define mod 1000000007

int main()
{
    long long a,b ;
    while(~scanf("%I64d %I64d",&a,&b)){
        //    printf("%I64d
",a*(a+1)/2) ;
        long long sum = (((a*(a+1)/2%mod)*b%mod+a)%mod*(b*(b-1)/2%mod))%mod ;
        printf("%I64d
",sum) ;
    }
    return 0 ;
}