一、PTA实验作业
题目1:7-2区位码输入法
1.本题PTA提交记录
2.设计思路
3.代码截图

4.本题调试过程碰到问题及PTA提交列表情况说明
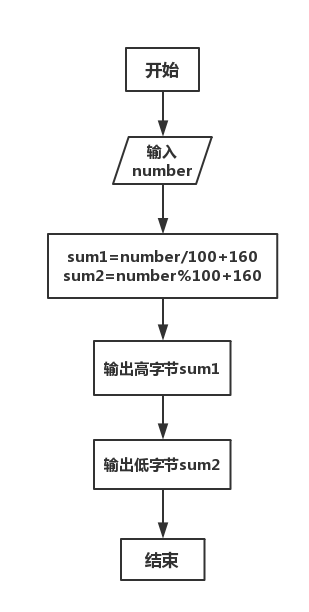
本来这道题看到题目我是惊慌失措的,还以为很难然后继续往下看看到了这个
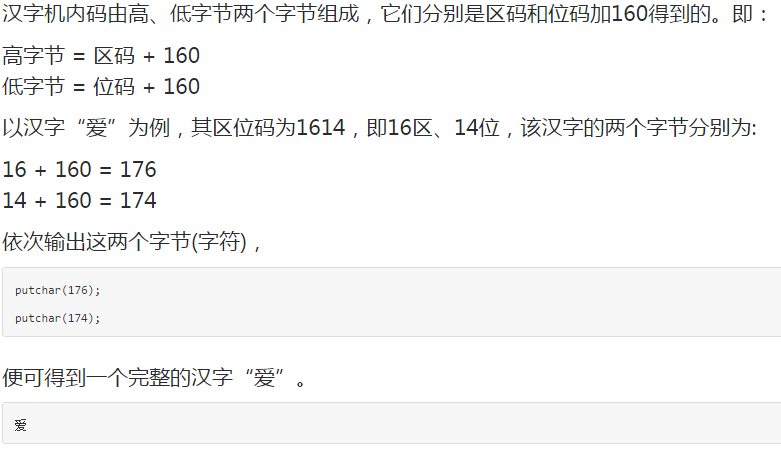
恍然大悟,写出代码之后出现了下面的问题:
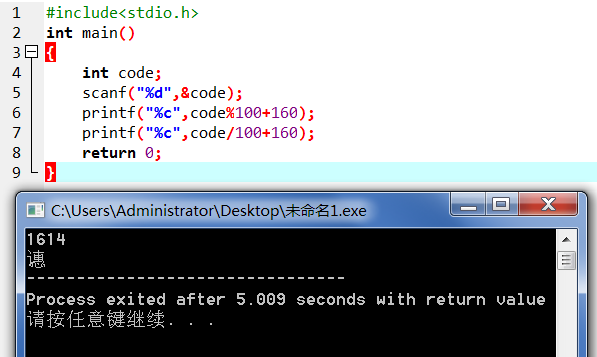
是高字节跟低字节的输出顺序错了,顺序调过来就好了。
题目2:7-6掉入陷阱的数字
1.本题PTA提交记录

2.设计思路
1.定义一个计算陷阱数的函数trap;
2.定义三个变量i,number,N,输入number的值;
3.进入循环:i=1,当i>0时,N=number,number=trap(number),输出i:number,当N=number时,程序结束;否,则i++,继续循环。
3.代码截图

4.本题调试过程碰到问题及PTA提交列表情况说明
编译错误是因为之前没什么思路,写到一半卡住了,就先提交去做别的事了。
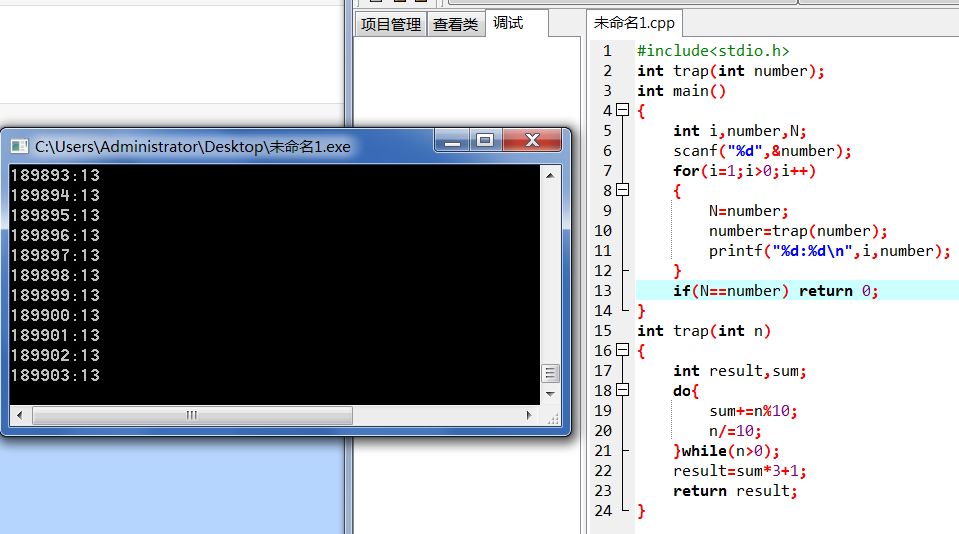
出现这个问题的原因是我把循环的结束条件放在了外面。
题目3.7-10简单计算器
1.本题PTA提交记录

2.设计思路
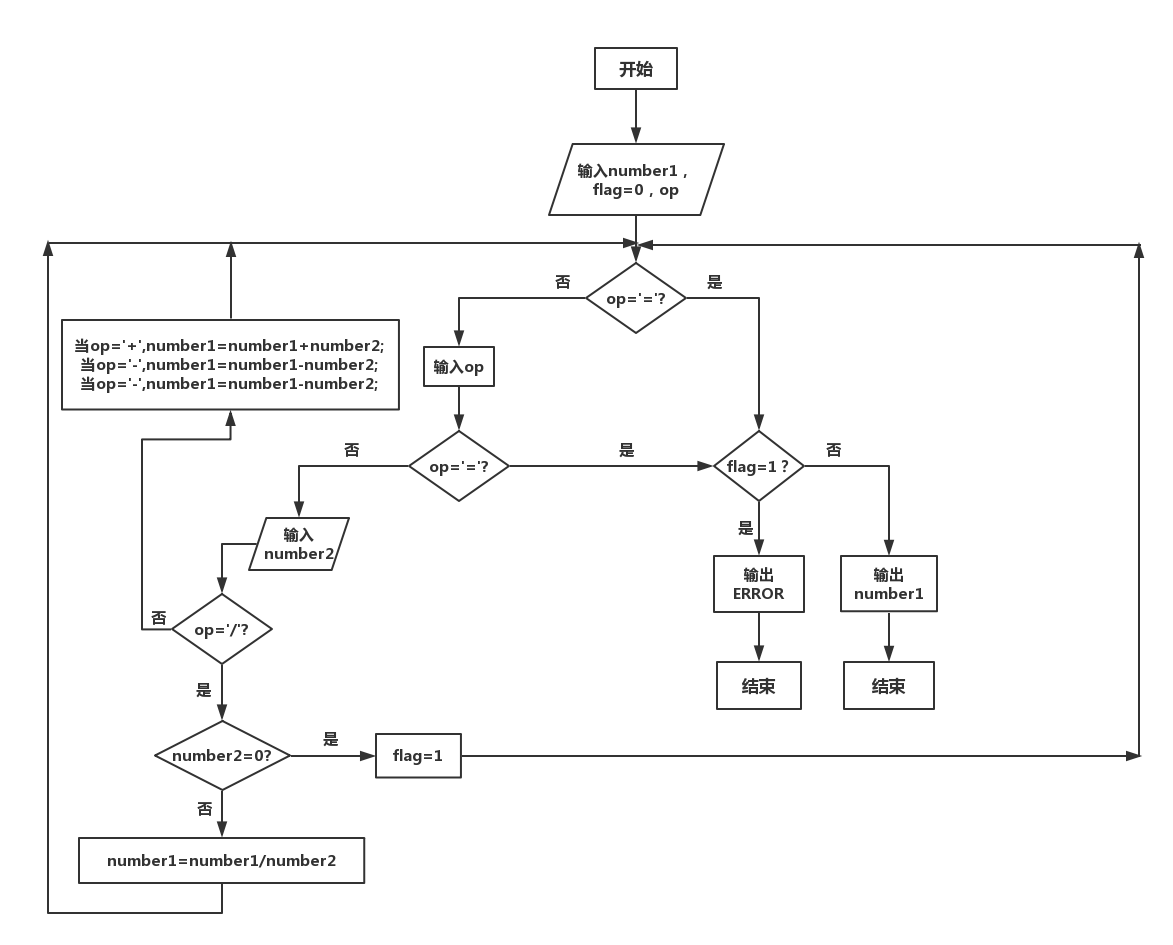
3.代码截图
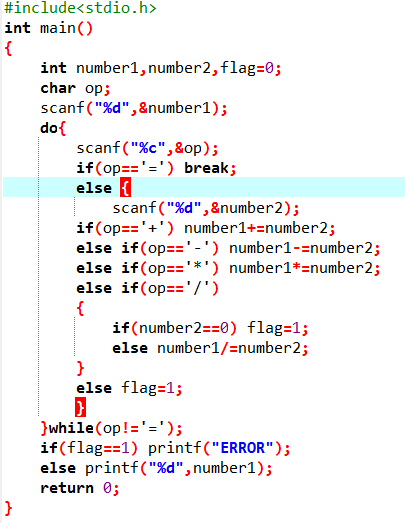
4.本题调试过程碰到问题及PTA提交列表情况说明
第一次错误是if里面的条件只用了一个等号,检查了很久才发现
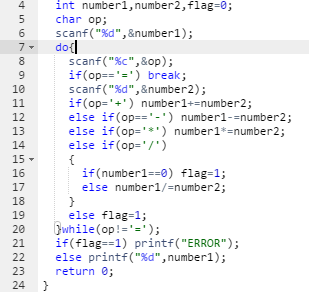
第二次则是判断输出“ERROR”的条件用了flag=0,反了,改为flag=1,时输出ERROR即可。
二、截图本周题目集的PTA最后排名

三、本周学习总结
1.你学会了什么?
1.1 一维数组如何定义、初始化?
- 定义:类型名 数组名 [数组长度];数组长度是一个常量
- 初始化:类型名 数组名 [数组长度]={初值表},例如inta a[10]={1,2,3,4,5,6,7,8,9,10}
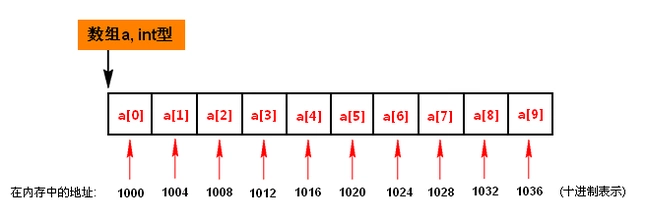
1.2 一维数组在内存中结构?可画图说明。数组名表示什么?
数组名是一个地址常量,存放数组内存空间的首地址。
1.3 为什么用数组?
可以减少定义变量带来的麻烦,便于数据的调用。
1.4 介绍选择法、冒泡法、直接插入排序如何排序?伪代码展示.
- 选择法排序
定义整型变量i,index,k,n,temp,index存放最小值所在的下标
定义数组a[10]
输入n
i=0
当i<n时,输入数, i递增
将输入的数依次赋给数组a的n个元素
k=0;k<n-1,用index来存放最小值所在下标
判断数组a中元素与a[index]大小
如果a[i]<a[index],index=i,最小元素与下标为k的元素交换
temp=a[index];
a[index]=a[k];
a[k]=temp;
输出排好后的n 个数组元素的值。 - 冒泡法排序
定义数组a[n]
定义整型变量i,j,temp,n
i=0
满足i<=n-1时
输入数
i++
将这组数据依次赋值给a[n]
判断相邻俩个数据,如果a[j]>a[j+1]
temp=a[j]
a[j]=a[j+1]
a[j+1]=temp
像这样的过程要重复n=q-i次
循环结束后输出新数组。 - 直接插入法排序
定义数组a[n]
定义整型变量i,j,k,temp
i=0;
满足i<=n-1时
输入数
i=0;
temp表示最小值的角标
判断数据a[j]和temp的大小
如果temp<a[j],a[j]=temp
通过a[k+1]=a[k]实现插入位置后的数据整体往右挪
重复n -1次,输出新数组。
1.5 介绍什么是二分查找法?它和顺序查找法区别?
- 对一组有序的数字中进行查找,传递相应的数据,比较与元数据相同的数据,查找到后返回对应数组下标
- 区别:顺序查找的特点是从第一个元素开始一个一个往下查找,如果和目标一致的元素,则查找成功,如果到最后一个元素仍没有目标元素,则查找失败。而二分查找就是从表的中间查找目标元素,如果找到一致元素,这查找成功,如果中间元素比目标元素小,仍用二分查找表的后半部分,反之,中间元素比目标元素大,则查找表的前半部分。
1.6 二维数组如何定义、初始化?
- 二维数组定义形式:类型名 数组名 [行长度][列长度]。
- 初始化:
(1)分行赋初值
一般形式:类型名 数组名 [行长度][列长度]={{初值表0},...,{{初值表k},...}
把初值表中的K中所有数据依次赋给第k行的元素。
(2)顺序赋值法
一般形式:类型名 数组名 [行长度][列长度] = {初值表}
根据数组元素在内存中的存放顺序,把初值表中的数据依次赋给元素。
1.7 矩阵转置怎么实现?方阵中:下三角、上三角、对称矩阵的行标i列标j的关系?请说明。
- 矩阵转置:以主对角线为对称轴,将所有元素互换位置;
- 下三角:i>=j;
- 上三角:i<=j;
- 对称矩阵:i==j;
1.8 二维数组一般应用在哪里?
- 二维表
- 矩阵
2.本周的内容,你还不会什么?
- 字符串的输入及判断极有难度,只有极个别情况的题目我才能写出来,一般写不出。。。
- 进制运算有点生疏。
- 对于二维数组的认识模糊,运用起来生涩。