洛谷3768：简单的数学题——题解

https://www.luogu.org/problemnew/show/P3768

题面来自洛谷，因为没用markdown所以直接截的图。

剩余的图是我用markdown写完然后截的图。

参考洛谷第一篇题解。

这个式子直观感受就需要莫比乌斯反演，大致的过程参考：BZOJ2693：jzptab

那么跳过暴力推式子，我们能够得到：

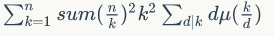
（如果你疑问为什么是miu(k/d)而不是miu(d)，其实二者皆可，但是为什么这么干请往下看）

显然可以分块O(sqrt(n))做，那么后面的那一串东西怎么做呢？

参考jzptab的想法的话我们知道后面的式子是积性函数可以O(n)筛出来。

emmm……虽然时间可能能过但是你空间也存不下啊，所以我们要舍弃这个想法。

我们有这样的式子：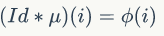

于是我们可以把后面的式子转换成这个，那么就变成了：

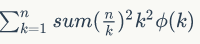
phi的前缀和可以杜教筛做，k^2也是分块求和。

具体的杜教筛式子可以看：http://blog.csdn.net/samjia2000/article/details/70147436

#include<cstdio>
#include<queue>
#include<map>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=4700050;
ll su[N],phi[N],sum[N],n,p,inv2,inv6;
bool he[N];
ll maxn=4700000;
map<ll,ll>mp;
inline ll s2(ll x){x%=p;return x*(x+1)%p*inv2%p;}
inline ll s3(ll x){x%=p;return x*(x+1)%p*(2*x+1)%p*inv6%p;}
inline ll sqr(ll x){x%=p;return x*x%p;}
ll pow(ll x,ll y){
    ll res=1;
    while(y){
    if(y&1)res=res*x%p;
    x=x*x%p;
    y>>=1;
    }
    return res;
}
void Euler(int n){
    int tot=0;
    phi[1]=1;he[1]=1;
    for(int i=2;i<=n;i++){
    if(!he[i]){
        su[++tot]=i;
        phi[i]=i-1;
    }
    for(int j=1;j<=tot;j++){
        if(i*su[j]>n)break;
        he[i*su[j]]=1;
        if(i%su[j]==0){
        phi[i*su[j]]=phi[i]*su[j]%p;
        break;
        }
        else phi[i*su[j]]=phi[i]*phi[su[j]]%p;
    }
    }
    for(int i=1;i<=n;i++){
    phi[i]=(phi[i-1]+phi[i]*sqr(i)%p)%p;
    }
    return;
}
ll f(ll x){
    if(x<=maxn)return phi[x];
    if(mp[x])return mp[x];
    ll res=sqr(s2(x));
    for(ll i=2,j;i<=x;i=j+1){
    j=x/(x/i);
    res-=f(x/i)*(s3(j)-s3(i-1))%p;
    res%=p;
    }
    return mp[x]=(res+p)%p;
    
}
int main(){
    scanf("%lld%lld",&p,&n);
    inv2=pow(2,p-2);inv6=pow(6,p-2);
    maxn=min(maxn,n);
    Euler(maxn);
    ll ans=0;
    for(ll i=1,j;i<=n;i=j+1){
    j=n/(n/i);
    ans+=(f(j)-f(i-1))%p*sqr(s2(n/i))%p;
    ans%=p;
    }
    printf("%lld
",(ans+p)%p);
    return 0;
}

+++++++++++++++++++++++++++++++++++++++++++

+本文作者：luyouqi233。 　　　　　　　　　　　　　　+

+欢迎访问我的博客：http://www.cnblogs.com/luyouqi233/+

+++++++++++++++++++++++++++++++++++++++++++