作为神秘奖励……?也是为了方便背。

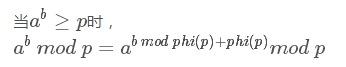
所有的除法都是向下取整。
数论函数:
((f*g)(n)=sum_{d|n}f(d)g(frac{n}{d}))
((Id*mu)(n)=sum_{d|n}mu(d)frac{n}{d}=phi(n))
筛法求积性函数:
int su[N],he[N],miu[N],phi[N],c[N],d[N],tot;
void Euler(int n){
miu[1]=d[1]=c[1]=phi[1]=1;
for(int i=2;i<=n;i++){
if(!he[i]){
su[++tot]=i;
miu[i]=-1;
phi[i]=i-1;
d[i]=2;
c[i]=1;
}
for(int j=1;j<=tot;j++){
int p=su[j];
if(i*p>n)break;
he[i*p]=1;
if(i%p==0){
miu[i*p]=0;
phi[i*p]=phi[i]*p;
d[i*p]=d[i]/(c[i]+1)*(c[i]+2);
c[i*p]=c[i]+1;
break;
}else{
miu[i*p]=miu[i]*miu[p];
phi[i*p]=phi[i]*phi[p];
d[i*p]=d[i]*d[p];
c[i*p]=1;
}
}
}
}
莫比乌斯反演:
(n=sum_{d|n}phi(d))
([n=1]=sum_{d|n}mu(d))
推导:
(sum_{i=1}^nsum_{j=1}^m[gcd(i,j)=p]=sum_{d=1}^{min(frac{n}{p},frac{m}{p})}mu(d)*frac{frac{n}{p}}{d}*frac{frac{m}{p}}{d})
例题+推导:BZOJ1101 & 洛谷3455:[POI2007]ZAP
(sum_{i=1}^nsum_{j=1}^mgcd(i,j)=sum_{d=1}^{min(n,m)}phi(d)*frac{n}{d}*frac{m}{d})
例题+推导:BZOJ2005:[Noi2010]能量采集
(sum_{i=1}^nsum_{j=1}^mlcm(i,j)=sum_{k=1}^{min(n,m)}sum(frac{n}{k})sum(frac{m}{k})sum_{d|k}d^2mu(d)frac{k}{d})
例题+推导:BZOJ2693:jzptab——题解
杜教筛:
令(M(n)=∑_{i=1}^nμ(i))
则(M(n)=1−∑_{i=2}^nM(frac{n}{i}))
令(S(n)=∑_{i=1}^nphi(i))
则(S(n)=∑_{i=1}^ni−∑_{i=2}^nS(frac{n}{i}))
推导:http://blog.csdn.net/samjia2000/article/details/70147436
+++++++++++++++++++++++++++++++++++++++++++
+本文作者:luyouqi233。 +
+欢迎访问我的博客:http://www.cnblogs.com/luyouqi233/ +
+++++++++++++++++++++++++++++++++++++++++++