http://acm.timus.ru/problem.aspx?space=1&num=1297
https://vjudge.net/problem/URAL-1297
给定一个字符串,求最长回文子串。
论文题,摘一下论文的图片,保证一下就看懂了。
(由于我摘不下来图片所以用了https://www.cnblogs.com/lidaxin/p/5002878.html的图片,代码也是参考的他)
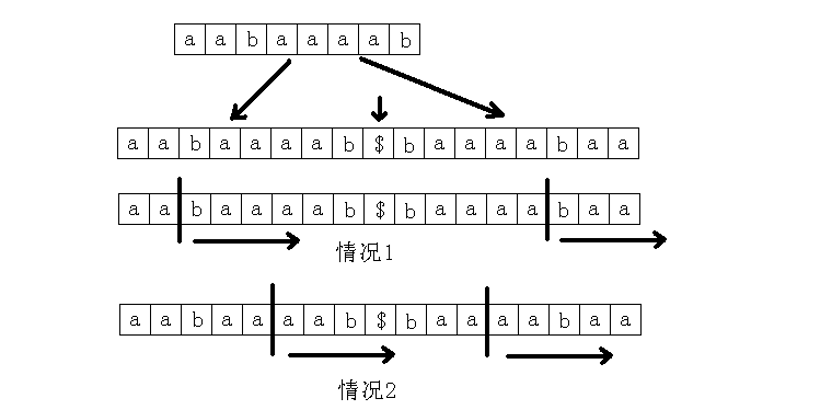
emm要是还没看懂的话稍微解释一下吧。
也就是说,实际上我们是把反串接到正串后面,然后后缀数组高度数组处理LSP(最大公共前缀),这样的公共前缀实际上就是回文串的一半。
当然是有上述的两种情况的,就是奇数长和偶数长的回文串,当然很好处理。
最后为了O(n),我们RMQ预处理一下即可。
#include<cstdio> #include<cmath> #include<iostream> #include<vector> #include<cstring> #include<algorithm> #include<cctype> using namespace std; const int N=3010; char s[N],ans[N]; int n,m,sa[N],rk[N],height[N],w[N],f[N][22],lg[N]; inline int qpow(int a){return 1<<a;} inline bool pan(int *x,int i,int j,int k){ int ti=i+k<n?x[i+k]:-1; int tj=j+k<n?x[j+k]:-1; return x[i]==x[j]&&ti==tj; } inline void SA_init(){ int *x=rk,*y=height,r=256; for(int i=0;i<r;i++)w[i]=0; for(int i=0;i<n;i++)w[s[i]]++; for(int i=1;i<r;i++)w[i]+=w[i-1]; for(int i=n-1;i>=0;i--)sa[--w[s[i]]]=i; r=1;x[sa[0]]=0; for(int i=1;i<n;i++) x[sa[i]]=s[sa[i]]==s[sa[i-1]]?r-1:r++; for(int k=1;r<n;k<<=1){ int yn=0; for(int i=n-k;i<n;i++)y[yn++]=i; for(int i=0;i<n;i++) if(sa[i]>=k)y[yn++]=sa[i]-k; for(int i=0;i<r;i++)w[i]=0; for(int i=0;i<n;i++)++w[x[y[i]]]; for(int i=1;i<r;i++)w[i]+=w[i-1]; for(int i=n-1;i>=0;i--)sa[--w[x[y[i]]]]=y[i]; swap(x,y);r=1;x[sa[0]]=0; for(int i=1;i<n;i++) x[sa[i]]=pan(y,sa[i],sa[i-1],k)?r-1:r++; } } inline void height_init(){ int i,j,k=0; for(i=1;i<=n;i++)rk[sa[i]]=i; for(i=0;i<n;i++){ if(k)k--; else k=0; j=sa[rk[i]-1]; while(s[i+k]==s[j+k])k++; height[rk[i]]=k; } } void st_init(){ for(int i=1;i<=n;i++){ f[i-1][0]=height[i]; lg[i]=lg[i-1]; if((1<<lg[i]+1)==i)lg[i]++; } for(int j=1;j<=lg[n];j++){ for(int i=0;i<n;i++){ if(i+qpow(j)-1>=n)break; f[i][j]=min(f[i][j-1],f[i+qpow(j-1)][j-1]); } } } int lcp(int a,int b){ int l=rk[a],r=rk[b]; if(r<l)swap(l,r); l--;r--; if(r<0)return 0; l++; int len=r-l+1; int k=lg[len]; int h=qpow(k); return min(f[l][k],f[r-h+1][k]); } int main(){ cin>>s; m=strlen(s),n=m*2+1; for(int i=0;i<m;i++)ans[i]=s[i]; s[m]=1; for(int i=m+1;i<n;i++){ s[i]=s[n-i-1]; } s[n++]=0; SA_init(); n--; height_init(); st_init(); int maxn=0,l,tmp; for(int i=0;i<n;i++){ tmp=lcp(i,n-i-1); if(2*tmp-1>maxn){ maxn=2*tmp-1; l=i-tmp+1; } tmp=lcp(i,n-i); if(2*tmp>maxn){ maxn=2*tmp; l=i-tmp; } } ans[l+maxn]='�'; printf("%s ",ans+l); return 0; }
+++++++++++++++++++++++++++++++++++++++++++
+本文作者:luyouqi233。 +
+欢迎访问我的博客:http://www.cnblogs.com/luyouqi233/+
+++++++++++++++++++++++++++++++++++++++++++