<泛> C++3D数学库设计详解 简单光学几何 && 随机向量生成

// 注：本内容为作者原创，禁止在其他网站复述内容以及用于商业盈利，如需引用，请标明出处：http://www.cnblogs.com/lv_anchoret/

 Preface

当初写这个库，是为了支持光线追踪的学习，所以，学完第一本书，这时候，我们整合一些物理光学方面的运算，封装到我们的泛型库里面

新库增加的目录：

--lvgm

　　----opticsfunc.hpp

　　----randfunc.cpp 

 Ready

需要大家拥有之前的向量库做支持

我们这一篇涉及到的库文件比较少

我们这一篇涉及到的基本是函数

据说，写库一般用hpp比较好，所以我们开始用hpp写C++泛型库

 theory

1.反射

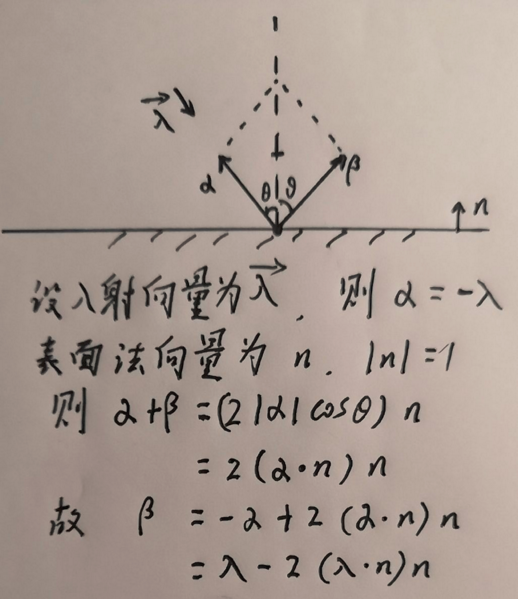
2.折射

公式中的η为相对折射率：n2/n1

而由于入射光线方向的随机性和eta的不同，可能导致 1-η*η*（1-cosθ1 * cosθ1）小于0，此时取根号毫无意义

而事实上，这也就是全反射现象。即：当光线从光密介质进入光疏介质中如果入射角大于某个临界值的时候，就会发生全反射现象。

该临界角即折射角为90°时对应的入射角，也就是cosθ2恰好等于0的时候

完整工程应用见https://www.cnblogs.com/lv-anchoret/p/10217719.html

3.单位球体内部随机向量

根据一个完全随机算法，确保生成一个0~1的随机数，用这样的三个随机数构建一个三维向量t

设 β = 2 * t - （1,1,1）

即保证了β的每一个分量均随机分布于0~1

这样的话，我们的向量β就等于时一个单位正方体之内的存在，而我们需要的是单位球体

所以，我们筛出单位球体外的，通过x^2 + y^2 + z^2 >= 1.0 式（a） 筛掉球体之外的

如果β = （x,y,z），也就是式（a）也就等价于 β·β >= 1.0

4. 生成单位球体表面随机点（向量）

推导详情见https://www.cnblogs.com/lv-anchoret/p/10518961.html

5.单位圆盘内的随机向量

和上面一样，减少一维即可

 实现

/// opticsfunc.hpp

// -----------------------------------------------------
// [author]        lv
// [ time ]        2019.1
// [brief ]        optics functions
//                reflect
//                refract
// -----------------------------------------------------

#pragma once

#include <lvgm	ype_vec	ype_vec.h>

namespace lvgm
{

    /*
    @in:    the Incident light
    @n:    the Surface normal
    @ret:    the reflected light
    */
template<typename T>
    const T reflect(const T& in, const T& n)
        {
        return in - 2 * dot(in, n)*n;
        }



    /*
    @in:    the Incident light
    @n:    the Surface normal
    @eta:    the Refractive indices
    @ret:    if it has a refracted light or not
    */
template<typename T>
    const bool refract(const T& in, const T& n, lvgm::precision eta, T& refracted)
        {
        if (typeid(T) == typeid(lvgm::vec2<int>))
            {
            std::cerr << "the refract is adapted to float and percision-upper
";
            return false;
            }

        T unitIn = in.ret_unitization();    //将入射光线单位化

        lvgm::precision cos1 = dot(-unitIn, n);
        lvgm::precision cos2 = 1. - eta*eta*(1. - cos1*cos1);
        if (cos2 > 0)
            {
            refracted = eta * unitIn + n * (eta * cos1 - std::sqrt(cos2));
            return true;
            }
        return false;
        }
}

#pragma once

#include <lvgm	ype_vec	ype_vec.h>
#include <random>

namespace lvgm
{

//@brief:    create a random number that from 0 to 1 completely
template<typename T = lvgm::precision>
    const T rand01()
        {
        if (typeid(T) == typeid(int))
            {
            std::cerr << "integer doesn't have a random number from 0 to 1
";
            throw "integer doesn't have a random number from 0 to 1
";
            }

        static std::mt19937 mt;
        static std::uniform_real_distribution<T> r;
        return r(mt);
        }


//@brief:    find a random point in unit_sphere
template<typename T = lvgm::precision>
    const lvgm::vec3<T> random_unit_sphere()
        {
        if (typeid(T) == typeid(int))
            {
            std::cerr << "integer doesn't have a random number from 0 to 1
";
            throw "integer doesn't have a random number from 0 to 1
";
            }

        lvgm::vec3<T> p;
        do
            {
            p = 2.0*lvgm::vec3<T>(rand01(), rand01(), rand01()) - lvgm::vec3<T>(1, 1, 1);
            } while (dot(p, p) >= 1.0);
        return p;
        }

//@brief:    find a random point on unit_sphere
template<typename T = lvgm::precision>
    const lvgm::vec3<T> random_on_sphere()
        {
        if (typeid(T) == typeid(int))
            {
            std::cerr << "integer doesn't have a random number from 0 to 1
";
            throw "integer doesn't have a random number from 0 to 1
";
            }

        double r1{ rand01() }, r2{ rand01() };
        return lvgm::vec3<T>
            {
            cos(2 * π * r1) * 2 * sqrt(r2 * (1 - r2)),
            sin(2 * π * r1) * 2 * sqrt(r2 * (1 - r2)),
            1 - 2 * r2
            };
        }


//@brief:    find a random point in unit_plane
template<typename T = lvgm::precision>
    const lvgm::vec2<T> random_unit_plane()
        {
        if (typeid(T) == typeid(int))
            {
            std::cerr << "integer doesn't have a random number from 0 to 1
";
            throw "integer doesn't have a random number from 0 to 1
";
            }

        lvgm::vec2<T> p;
        do
            {
            p = 2.0*lvgm::vec2<T>(rand01(), rand01()) - lvgm::vec2<T>(1, 1);
            } while (dot(p, p) >= 1.0);
        return p;
        }

}//lvgm namespace

感谢您的阅读，生活愉快~