2019年11月23日开发手记

提取外切轮廓目前没有什么现成的API可用，所以也得自己写一个，考虑到经过滤波后的目标图像为点集状态，所以打算采用聚类算法，经过比较，决定选择聚类算法中的k-means算法作为运动区域中心点检测算法。

k-means算法：

算法步骤：

(1) 首先我们选择一些类/组，并随机初始化它们各自的中心点。中心点是与每个数据点向量长度相同的位置。这需要我们提前预知类的数量(即中心点的数量)。

(2) 计算每个数据点到中心点的距离，数据点距离哪个中心点最近就划分到哪一类中。

(3) 计算每一类中中心点作为新的中心点。

(4) 重复以上步骤，直到每一类中心在每次迭代后变化不大为止。也可以多次随机初始化中心点，然后选择运行结果最好的一个。

代码例程：

# -*- coding:utf-8 -*-
import re
import math
import numpy as np
import pylab as pl
data = 
"1,0.697,0.46,Y,
2,0.774,0.376,Y,
3,0.634,0.264,Y,
4,0.608,0.318,Y,
5,0.556,0.215,Y,
6,0.403,0.237,Y,
7,0.481,0.149,Y,
8,0.437,0.211,Y,
9,0.666,0.091,N,
10,0.243,0.267,N,
11,0.245,0.057,N,
12,0.343,0.099,N,
13,0.639,0.161,N,
14,0.657,0.198,N,
15,0.36,0.37,N,
16,0.593,0.042,N,
17,0.719,0.103,N"
#定义一个西瓜类，四个属性，分别是编号，密度，含糖率，是否好瓜
class watermelon:
    def __init__(self, properties):
        self.number = properties[0]
        self.density = float(properties[1])
        self.sweet = float(properties[2])
        self.good = properties[3]

#数据简单处理
a = re.split(',|
|	', data.strip(" "))
dataset = []     #dataset:数据集
for i in range(int(len(a)/4)):
    temp = tuple(a[i * 4: i * 4 + 4])
    dataset.append(watermelon(temp))

#计算欧几里得距离,a,b分别为两个元组
def dist(a, b):
    return math.sqrt(math.pow(a[0]-b[0], 2)+math.pow(a[1]-b[1], 2))


#算法模型
def k_means(k, dataset, max_iter):
    U = np.random.choice(dataset, k)#从a中随机选取3个值
    U = [(wm.density, wm.sweet) for wm in U]    #均值向量列表
    C = [[] for i in range(k)]      #初始化分类列表
    U_update = []                   #均值向量更新列表
    while max_iter > 0:
        #分类
        for i in dataset:
            temp = np.argmin([dist((i.density, i.sweet), U[j]) for j in range(len(U))])#返回最小值的下标
            C[temp].append(i)
        #更新均值向量
        for i in range(k):
            ui_density = 0.0
            ui_sweet = 0.0
            for j in C[i]:
                ui_density += j.density
                ui_sweet += j.sweet
            U_update.append((ui_density/len(C[i]), ui_sweet/len(C[i])))#求得均值
        #每五次输出一次分类图
        if max_iter % 5 == 0:
            draw(C, U)
        #比较U和U_update
        if U == U_update:
            break
        U = U_update
        U_update = []
        C = [[] for i in range(k)]
        max_iter -= 1

    return C, U

#画图
def draw(C, U):
    colValue = ['r', 'y', 'g', 'b', 'c', 'k', 'm']
    for i in range(len(C)):
        coo_X = []    #x坐标列表
        coo_Y = []    #y坐标列表
        for j in range(len(C[i])):
            coo_X.append(C[i][j].density)
            coo_Y.append(C[i][j].sweet)
        pl.scatter(coo_X, coo_Y, marker='x', color=colValue[i%len(C)], label=str(i))
    #展示均值向量
    U_x = []
    U_y = []
    for i in U:
        U_x.append(i[0])
        U_y.append(i[1])
    pl.scatter(U_x, U_y, marker='.', color=colValue[6], label="avg_vector")
    pl.legend(loc='upper right')
    pl.show()

C, U = k_means(3, dataset, 30)
draw(C, U)

输出结果：

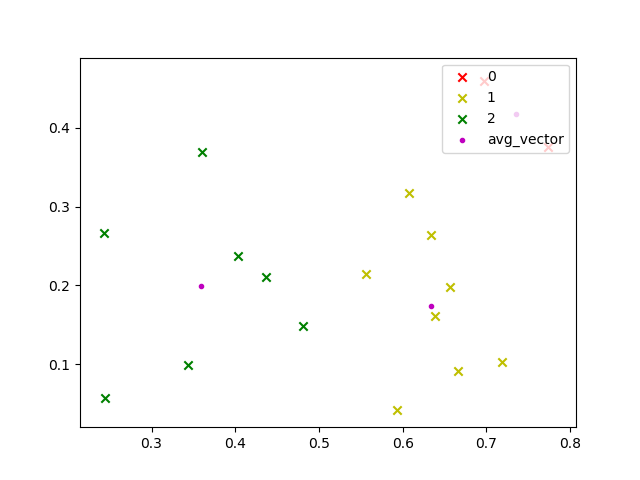
第一张图是最开始初始化的样子，均值向量和样本点重合。 第二张图为最后聚类结果。

目前的打算是先用cv2.findContours得到轮廓的点集，再用k-means算法得到每个轮廓的几何中心，继而根据得到的多个几何中心绘制矩形，从而得到目标外切轮廓。