买书方案01

设计思想：

本次购买书的方案是一次分情况讨论实验，上课老师讲用枚举的情况分析先从6本书开始找购买方案的规律发现，买书方案在10种情况之内：

6本书=5本书+1本书；

7本书=5本书+2本书；

8本书=4本书+4本书；

9本书=5本书+4本书；

10本书=5本书+5本书；

这种方案最合适，只要用买书的数量取余和取整，求每种情况所花的钱就可以；

//信1301-2 20133056 吕兰兰
// 题目：根据购买的卷数以及本数，会对应不同折扣规则情况。单数一本书只会对应一个折扣规则，例如购买了两本卷1，一本卷2，
//则可以享受5%的折扣，另外一本卷一则不享受优惠。
 
#include<iostream> 
using namespace std;
void book_buy(int book_quantity)
{
//    int book_quantity;//要购买的书的数量； 
     int book_remainder;//根据余数选择的购买的方式 
     int book_count;//计数 
     double book_money1; 
     double book_money2;
     double book_money;//总共花费的钱数 
     book_remainder=book_quantity%10;
     book_count=book_quantity/10; 
     //整数部分的购买方式为：五五购买
    book_money1=(5*8*0.75*2)*book_count;// 
    cout<<"购买"<<book_count<<"整套书（每套书10本） "; 
     //每种情况所要花的钱数 
    switch(book_remainder)
    {
        case 0: book_money2=0; break;
        case 1: cout<<" 1 本书";
        book_money2=8*1;
        break;
        case 2: cout<<" 2 本书";
        book_money2=8*2*0.95;
        break;
        case 3:cout<<" 3 本书";
         book_money2=8*3*0.9;
         break;
        case 4: cout<<" 4 本书";
        book_money2=8*4*0.8;
        break;
        case 5: cout<<" 5 本书" ;
        book_money2=8*5*0.75;
        break;
        case 6: cout<<" 6 本书";
        book_money2=8*5*0.75+8*1;
        break;
        case 7: cout<<" 7 本书";
        book_money2=8*5*0.75+8*2*0.95;
        break;
        case 8:cout<<" 8 本书";
         book_money2=4*8*0.8*2;
         break;
        case 9:cout<<" 9 本书";
         book_money2=5*8*0.75+4*8*0.8;
         break;
        
    }
    book_money=book_money1+book_money2;//计算总共花的钱数 
    cout<<endl; 
     cout<<"总共的花费为：";
    cout<<book_money;
    cout<<"元。";
 } 
 int main()
 {
     double book_quantity; 
     cout<<"请输入要购买的数量：";
     cin>>book_quantity;
     //判断输入是否正确 
     while (book_quantity<0||(book_quantity!=(int)book_quantity))
     {
         cout<<"Error!";
         cout<<"请输入大于零的整数量：";
         cin>>book_quantity;
    }     
    //调用子函数 
     book_buy(book_quantity);
 }

代码截图：

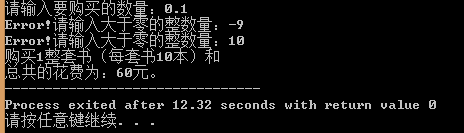
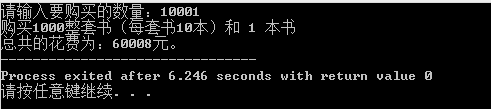
个人总结：

本次实验实验思路老师上课已将，实现起来比较简单，但是购买数量输入的判断对于数量超出一定范围不能实现判断并且对于非数字的输入判断还不能实现，这次实验的难点我认为就是在此，下来就此问题会好好查看相关资料看能否解决；