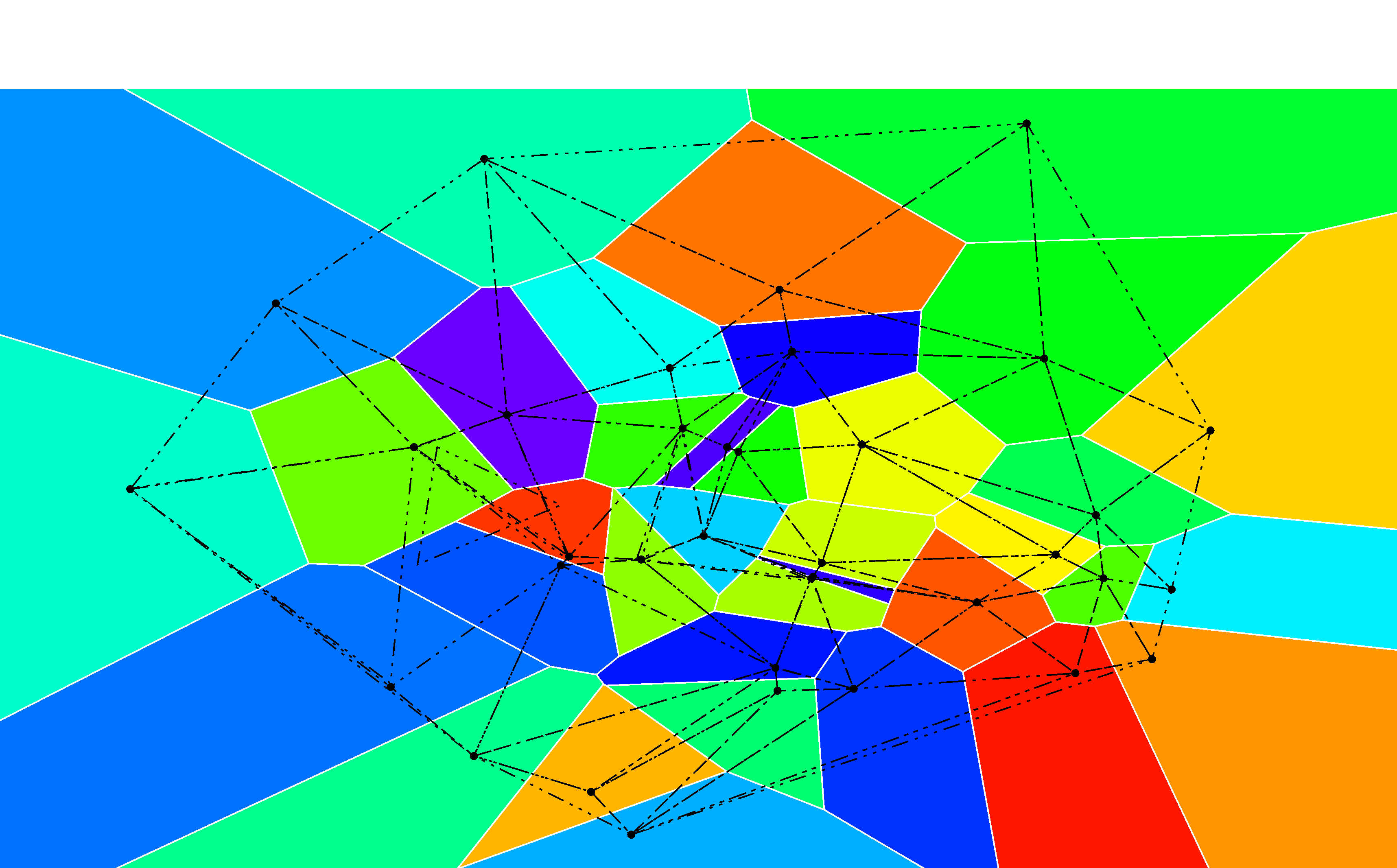
结果图:
附加源码:
PRO testVoronoi
idx = 0
; 创建离散点
CASE idx OF
; 随机离散点
0: BEGIN
N = 36
X = RANDOMN(seed, N)
Y = RANDOMN(seed, N)
END
; 规则离散点
1: BEGIN
X = REBIN(INDGEN(6)+10, 36,1)
Y = REFORM(REBIN(INDGEN(6)+10, 6,6),36,1)
N = N_ELEMENTS(X)
END
; 较规则离散点
2: BEGIN
X = REBIN(INDGEN(6)+10, 36,1)+ RANDOMU(seed, 36,1)
Y = REFORM(REBIN(INDGEN(6)+10, 6,6),36,1)+ RANDOMU(seed, 36,1)
N = N_ELEMENTS(X)
END
ELSE:
ENDCASE
; 构建Delaunay三角网
TRIANGULATE, X, Y, tr, CONN=C
; 绘制离散点
Points = PLOT(x, y, $
LINESTYLE=6, $
SYMBOL='o', SYM_COLOR='black', $
SYM_SIZE=0.5, $
/SYM_FILLED, SYM_FILL_COLOR='black', $
AXIS_STYLE=4, $
MARGIN=[0,0,0,0], $
WINDOW_TITLE='泰森多边形')
FOR I=0, N-1 DO BEGIN
; 获取第i个泰森多边形:
VORONOI, X, Y, I, C, Xp, Yp
; 快速可视化绘制
; 创建Polygon函数中的CONNECTIVITY关键字,指定连通性
n=N_ELEMENTS(Xp)
con = [n,INDGEN(n)]
; 绘制泰森多边形
poly = POLYGON(Xp,Yp,/data,CONNECTIVITY=con, /current, $
FILL_BACKGROUND=1, FILL_COLOR=I*7+5, RGB_TABLE=25, $
COLOR='white')
ENDFOR
; 绘制三角网,如果不想绘制,把这几行注释即可
n_Tr = (SIZE(tr, /DIMENSIONS))[1]
FOR i = 0,n_Tr-1 DO BEGIN
tri = POLYGON(X[tr[*,i]], Y[tr[*,i]], CONNECTIVITY=[3,0,1,2], $
/current, color = 'black', /data, FILL_BACKGROUND=0, $
LINESTYLE=4)
ENDFOR
; 将离散点置顶显示
Points.ORDER, /BRING_TO_FRONT
END