题意:餐厅每天会需要用Ri块新的餐巾 用完后也会产生Ri块旧的餐巾
每天购买新的餐巾单价p元 每天产出的旧餐巾可以送到快洗部花费每张c1元 在i + v1天可以使用
也可以花费c2元每张送到慢洗部 在i + v2天可以使用 问n天的最小花费
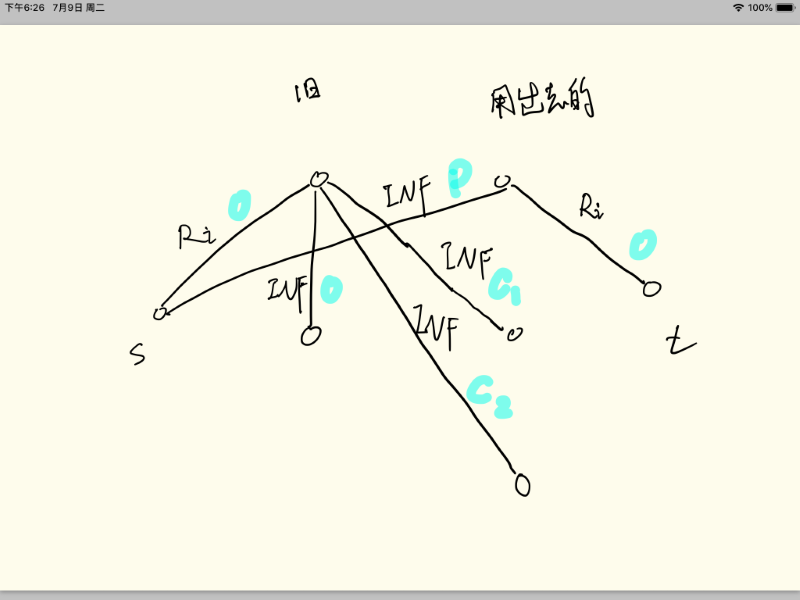
题解:把每天拆点 分为用出去的 和得到的旧餐巾
s -> 用出去的 表示每天可以买新的
用出去的-> t 表示每天一定会用Ri张纸巾
s-> 旧 表示每天一定会产生Ri块旧的纸巾
特判一下后 旧的按题意可以送去快洗和慢洗 然后今天没用完的旧的 明天也可以用

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int INF = 0x3f3f3f3f; int n, v1, c1, v2, c2, p; int cnt, s, t; int q[2005]; ll mincost, maxflow; struct node { int to, nex, val, cost; }E[25005]; int head[4005]; int cur[4005]; void addedge(int x, int y, int va, int cos) { E[++cnt].to = y; E[cnt].nex = head[x]; head[x] = cnt; E[cnt].val = va; E[cnt].cost = cos; E[++cnt].to = x; E[cnt].nex = head[y]; head[y] = cnt; E[cnt].val = 0; E[cnt].cost = -cos; } int inque[4005]; int dis[4005]; int vis[4005]; bool spfa() { for(int i = 0; i <= (n << 1 | 1); i++) dis[i] = INF, inque[i] = 0, cur[i] = head[i], vis[i] = 0; queue<int> que; que.push(s); dis[s] = 0; inque[s] = 1; while(!que.empty()) { int u = que.front(); que.pop(); inque[u] = 0; for(int i = head[u]; i; i = E[i].nex) { int v = E[i].to; if(E[i].val > 0 && dis[v] > dis[u] + E[i].cost) { dis[v] = dis[u] + E[i].cost; if(!inque[v]) { que.push(v); inque[v] = 1; } } } } if(dis[t] != INF) return true; return false; } int dfs(int x, int flow) { if(x == t) { vis[t] = 1; return flow; } vis[x] = 1; int used = 0; int rflow = 0; for(int i = cur[x]; i; i = E[i].nex) { cur[x] = i; int v = E[i].to; if(E[i].val > 0 && dis[v] == dis[x] + E[i].cost && (!vis[v] || v == t)) { if(rflow = dfs(v, min(flow - used, E[i].val))) { used += rflow; E[i].val -= rflow; E[i ^ 1].val += rflow; mincost += 1LL * rflow * E[i].cost; if(used == flow) break; } } } return used; } void dinic() { while(spfa()) { vis[t] = 1; while(vis[t]) { vis[t] = 0; dfs(s, INF); } } } int main() { mincost = maxflow = 0; cnt = 1; scanf("%d", &n); for(int i = 1; i <= n; i++) scanf("%d", &q[i]), maxflow += 1LL * q[i]; s = 0; t = 1; scanf("%d%d%d%d%d", &p, &v1, &c1, &v2, &c2); for(int i = 1; i <= n; i++) { addedge(s, i << 1, q[i], 0); addedge(i << 1 | 1, t, q[i], 0); addedge(s, i << 1 | 1, INF, p); if(i + v1 <= n) addedge(i << 1, (i + v1) << 1 | 1, INF, c1); if(i + v2 <= n) addedge(i << 1, (i + v2) << 1 | 1, INF, c2); if(i + 1 <= n) addedge(i << 1, (i + 1) << 1, INF, 0); } dinic(); printf("%lld ", mincost); return 0; }
