算法：Number of 1 Bits 收藏

Approach #1 (Loop and Flip) [Accepted]

Algorithm

The solution is straight-forward. We check each of the 3232 bits of the number. If the bit is 11, we add one to the number of 11-bits.

We can check the i^{th}i​th​​ bit of a number using a bit mask. We start with a mask m=1m=1, because the binary representation of 11 is,

0000 0000 0000 0000 0000 0000 0000 00010000 0000 0000 0000 0000 0000 0000 0001

Clearly, a logical AND between any number and the mask 11 gives us the least significant bit of this number. To check the next bit, we shift the mask to the left by one.

0000 0000 0000 0000 0000 0000 0000 00100000 0000 0000 0000 0000 0000 0000 0010

And so on.

Java

public int hammingWeight(int n) {
    int bits = 0;
    int mask = 1;
    for (int i = 0; i < 32; i++) {
        if ((n & mask) != 0) {
            bits++;
        }
        mask <<= 1;
    }
    return bits;
}

Complexity Analysis

The run time depends on the number of bits in nn. Because nn in this piece of code is a 32-bit integer, the time complexity is O(1)O(1).

The space complexity is O(1)O(1), since no additional space is allocated.

---

Approach #2 (Bit Manipulation Trick) [Accepted]

Algorithm

We can make the previous algorithm simpler and a little faster. Instead of checking every bit of the number, we repeatedly flip the least-significant 11-bit of the number to 00, and add 11 to the sum. As soon as the number becomes 00, we know that it does not have any more 11-bits, and we return the sum.

The key idea here is to realize that for any number nn, doing a bit-wise AND of nn and n - 1n−1 flips the least-significant 11-bit in nn to 00. Why? Consider the binary representations of nn and n - 1n−1.

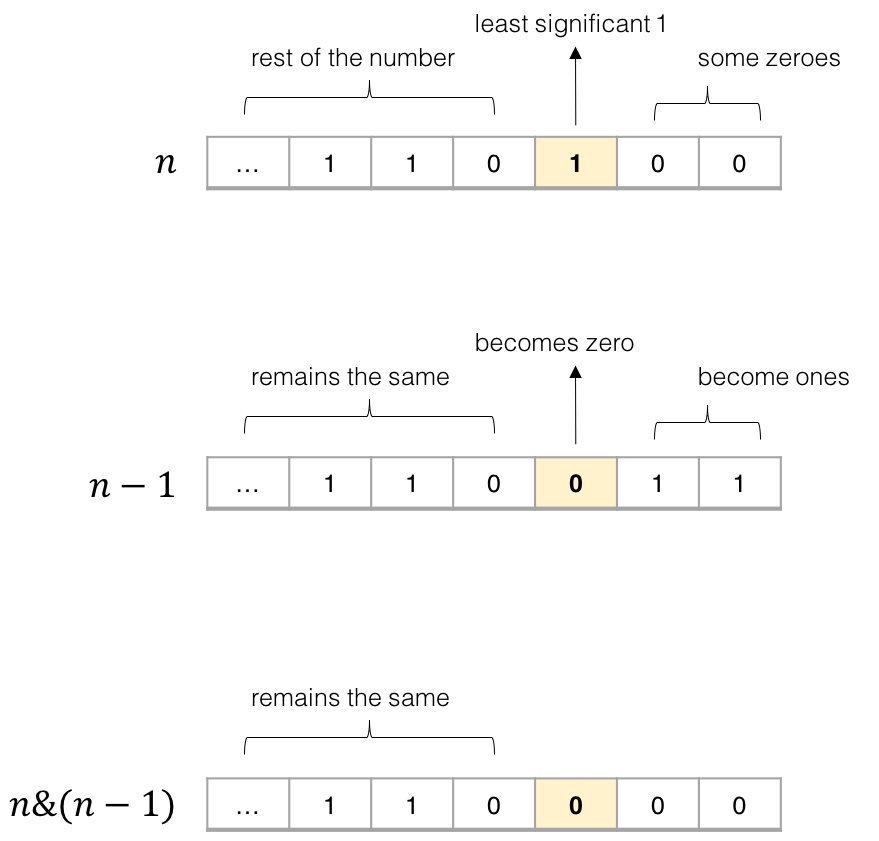
Figure 1. AND-ing nn and n-1n−1 flips the least-significant 11-bit to 0.

In the binary representation, the least significant 11-bit in nn always corresponds to a 00-bit in n - 1n−1. Therefore, anding the two numbers nn and n - 1n−1 always flips the least significant 11-bit in nn to 00, and keeps all other bits the same.

Using this trick, the code becomes very simple.

Java

public int hammingWeight(int n) {
    int sum = 0;
    while (n != 0) {
        sum++;
        n &= (n - 1);
    }
    return sum;
}

Complexity Analysis

The run time depends on the number of 11-bits in nn. In the worst case, all bits in nn are 11-bits. In case of a 32-bit integer, the run time is O(1)O(1).

The space complexity is O(1)O(1), since no additional space is allocated.

Analysis written by: @noran.