CRB and Puzzle
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Submission(s): 483 Accepted Submission(s): 198
Problem Description
CRB is now playing Jigsaw Puzzle.
There are
He can assemble one piece to the right side of the previously assembled one.
For each kind of pieces, only restricted kinds can be assembled with.
How many different patterns he can assemble with at most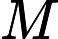

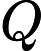


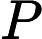
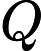
There are

He can assemble one piece to the right side of the previously assembled one.
For each kind of pieces, only restricted kinds can be assembled with.
How many different patterns he can assemble with at most
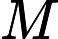

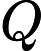


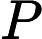
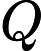
Input
There are multiple test cases. The first line of input contains an integer 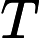
The first line contains two integers
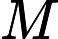
Then
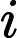
k









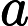

Here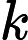
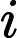
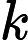
1 ≤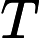
1 ≤
1 ≤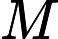
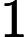
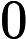
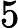
0 ≤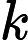

1 ≤

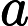


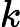
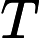
The first line contains two integers

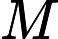
Then

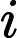
k










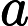

Here
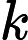
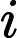
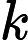
1 ≤
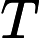
1 ≤

1 ≤
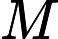
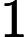
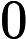
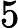
0 ≤
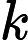

1 ≤


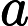


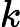
Output
For each test case, output a single integer - number of different patterns modulo 2015.
Sample Input
1 3 2 1 2 1 3 0
Sample Output
6Hintpossible patterns are ∅, 1, 2, 3, 1→2, 2→3
Author
KUT(DPRK)
解题思路:
DP方程非常easy想到 dp[i][j] = sum(dp[i-1][k] <k,j>连通) 构造矩阵用矩阵高速幂加速就可以。
DP方程非常easy想到 dp[i][j] = sum(dp[i-1][k] <k,j>连通) 构造矩阵用矩阵高速幂加速就可以。
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <queue>
#include <set>
#include <map>
#include <algorithm>
#define LL long long
using namespace std;
const int MAXN = 55 + 10;
const int mod = 2015;
int n, m;
struct Matrix
{
int m[MAXN][MAXN];
Matrix(){memset(m, 0, sizeof(m));}
Matrix operator * (const Matrix &b)const
{
Matrix res;
for(int i=1;i<=n+1;i++)
{
for(int j=1;j<=n+1;j++)
{
for(int k=1;k<=n+1;k++)
{
res.m[i][j] = (res.m[i][j] + m[i][k] * b.m[k][j]) % mod;
}
}
}
return res;
}
};
Matrix pow_mod(Matrix a, int b)
{
Matrix res;
for(int i=1;i<=n+1;i++) res.m[i][i] = 1;
while(b)
{
if(b & 1) res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
Matrix a, b;
scanf("%d%d", &n, &m);
for(int i=1;i<=n+1;i++) a.m[i][n+1] = 1;
for(int i=1;i<=n;i++)
{
int x, k;scanf("%d", &k);
for(;k--;)
{
scanf("%d", &x);
a.m[i][x] = 1;
}
}
a = pow_mod(a, m);
int ans = 0;
for(int i=1;i<=n+1;i++) ans = (ans + a.m[i][n+1]) % mod;
printf("%d
", ans);
}
return 0;
}