作业五——线性回归算法

【1.总结】

线性回归可以理解为：在N维空间中找一个形式像直线方程（y=ax+b）一样的函数来拟合数据。

因此，线性回归包括：

　　单元（单因素）线性回归

　　多元（多因素）线性回归

而在构建线性回归模型的过程中，我们需要选择最合适的那条线，即预测结果与真实结果误差最小，这里就涉及到一个概念：损失函数（最小二乘法）。

损失函数是模型输出和观测结果间概率分布差异的量化

 其实质为欧式距离加和。

李航-《统计学习方法》中总结了“算法-策略-优化”模型，以下归纳线性回归算法的思想。

 　　（1）所谓正规方程，

 　　（2）所谓梯度下降，是对自变量进行不断的更新（针对w和b求偏导），使得目标函数不断逼近最小值的过程

【2.思考线性回归算法可以用来做什么？】

线性回归算法主要是学习已有数据集，预测后续发展。如可以根据气候条件等因素预测某地区日出时间。

【3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）】

1）获取数据

import pandas as pd
import matplotlib.pyplot as plt


points = pd.read_csv("E:/机器学习/机器学习及其算法/data/data.csv")
# points
# 提取points中的两列数据，分别作为x,y
x = points.iloc[:, 0]
y = points.iloc[:, 1]
x = x.values.reshape(1, -1)
y = y.values.reshape(1, -1)


# 用plt画出散点图
plt.scatter(x, y)
plt.show()

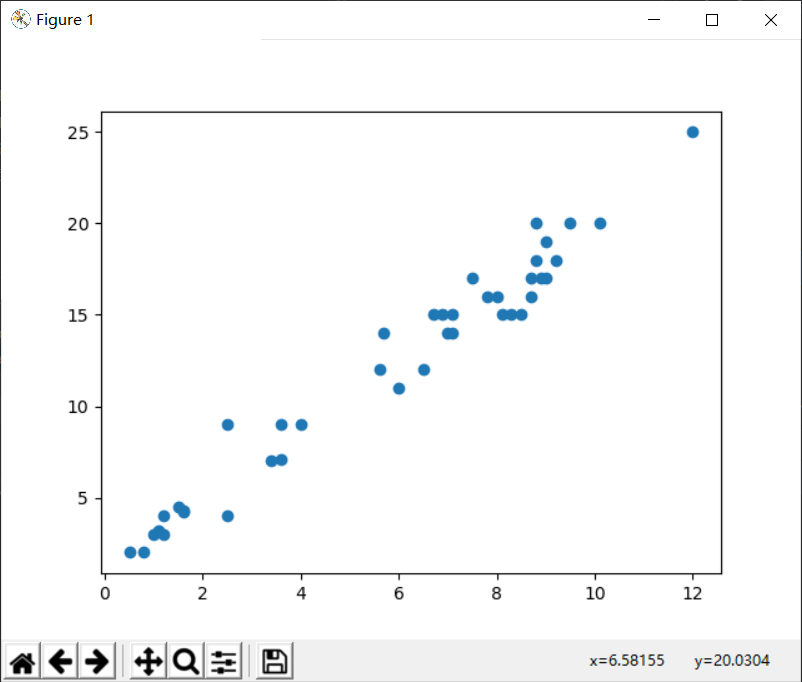
2）构造函数

 · 损失函数

# 损失函数是系数的函数，另外还要传入数据的x,y
def compute_cost(w, b, points):
    total_cost = 0
    m = float(len(points))
    for i in range(len(points)):
        x = points.iloc[i, 0]
        y = points.iloc[i, 1]
        total_cost += (y - w * x - b) ** 2
    return total_cost / m  # 一除都是浮点

 · 优化器——梯度下降

def grad_desc(points, initial_w, initial_b, alpha, num_iter):
    # alpha为学习率，num_iter为迭代次数
    w = initial_w
    b = initial_b
    # 定义一个list保存所有的损失函数值，用来显示下降过程。
    cost_list = []
    for i in range(num_iter):
        cost_list.append(compute_cost(w, b, points))
        w, b = step_grad_desc(w, b, alpha, points)
    return [w, b, cost_list]

 · 参数更新——计算梯度

def step_grad_desc(current_w, current_b, alpha, points):
    sum_grad_w = 0
    sum_grad_b = 0
    m = float(len(points))
    # 对每个点代入公式求和
    for i in range(len(points)):
        x = points.iloc[i, 0]
        y = points.iloc[i, 1]
        sum_grad_w += (current_w * x + current_b - y) * x
        sum_grad_b += current_w * x + current_b - y
    # 用公式求当前梯度
    grad_w = 2 / m * sum_grad_w
    grad_b = 2 / m * sum_grad_b

    # 梯度下降，更新当前的w和b
    updated_w = current_w - alpha * grad_w
    updated_b = current_b - alpha * grad_b
    return updated_w, updated_b

 · 初始化数据

alpha = 0.0000001
initial_w = 0
initial_b = 0
num_iter = 20

 · 调用函数——计算w、b和损失值

w, b, cost_list = grad_desc(points, initial_w, initial_b, alpha, num_iter)
print("w is :", w)
print("b is :", b)

cost = compute_cost(w, b, points)

print("cost_list:", cost_list)
print("cost is:", cost)
pred_y = w * x + b
plt.plot(cost_list)

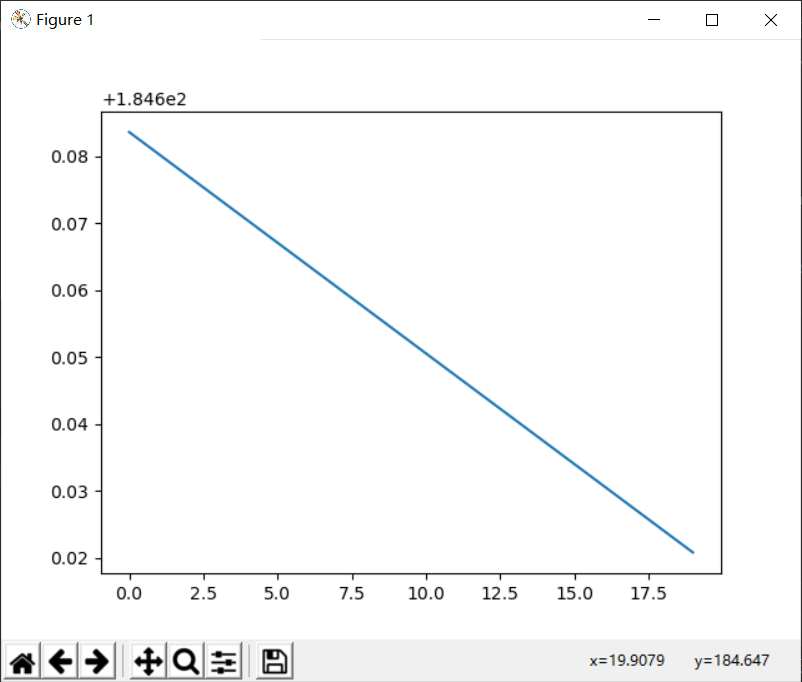
  · 可视化——预测值与原始值

plt.scatter(x, y)
plt.plot(x, pred_y, c='r')
plt.show()

 

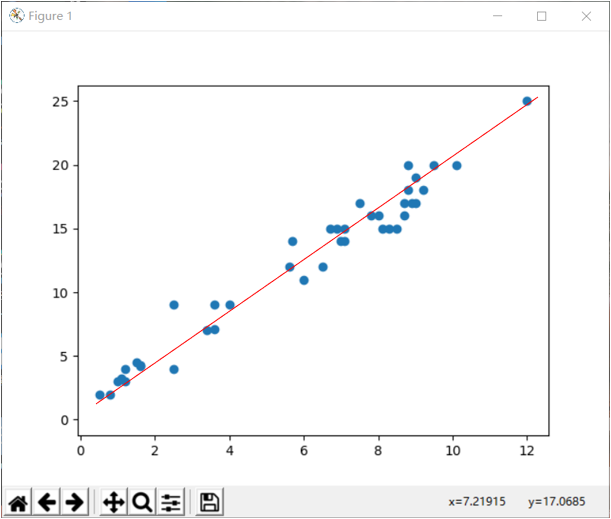
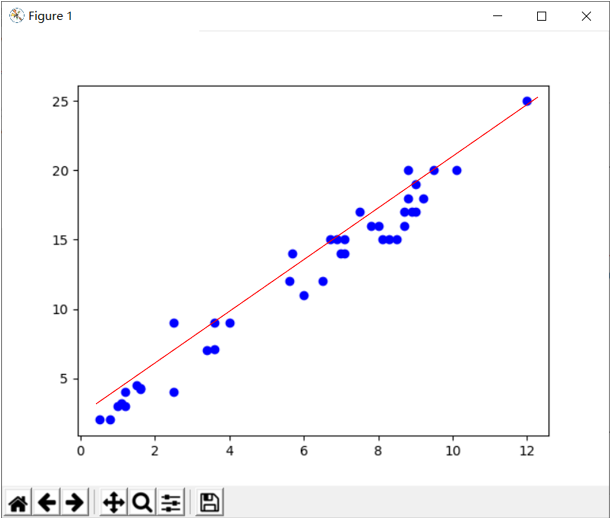
 3）对比sklearn.LinearRegression

from sklearn.linear_model import LinearRegression

model = LinearRegression()
model.fit(x, y)
pre = model.predict(x)
plt.scatter(x, y, c='b')
plt.plot(x, pre, c='r')
plt.show()

学习资料