1.简述人工智能、机器学习和深度学习三者的联系与区别。
人工智能是一个大的发展中的概念,其中包括包括专家系统、机器学习、进化计算、模糊逻辑、计算机视觉、自然语言处理、推荐系统等。即机器学习是实现人工智能的其中一个方法,而深度学习是机器学习所使用的一种算法。
总结:人工智能 > 机器学习 > 深度学习
2. 全连接神经网络与卷积神经网络的联系与区别。
在全连接神经网络中,每两层之间的节点都有边相连。(不适用图片识别)
神经元都是拉成一列排列,对于图片的像素空间信息会丢失。
卷积神经网络也是通过一层一层的节点组织起来的,对于卷积神经网络,相邻两层之间只有部分节点相连。在卷积神经网络的前几层中,每一层的节点都被组织成一个三维矩阵。前几层中每一个节点只和上一层中部分节点相连。
卷积神经网络结构:
- 1、输入层
- 2、卷积层
- 3、池化层(Pooling)
- 4、全连接层
- 5、softmax层
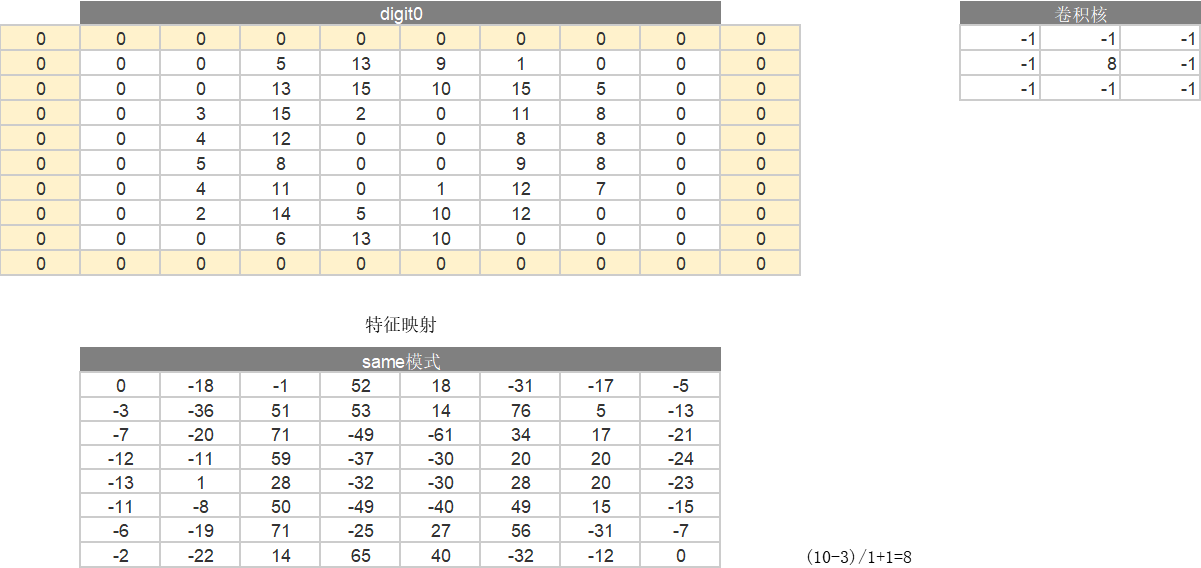
3.理解卷积计算。
以digit0为例,进行手工演算。
from sklearn.datasets import load_digits #小数据集8*8
digits = load_digits()
|
0 |
0 |
5 |
13 |
9 |
1 |
0 |
0 |
|
0 |
0 |
13 |
15 |
10 |
15 |
5 |
0 |
|
0 |
3 |
15 |
2 |
0 |
11 |
8 |
0 |
|
0 |
4 |
12 |
0 |
0 |
8 |
8 |
0 |
|
0 |
5 |
8 |
0 |
0 |
9 |
8 |
0 |
|
0 |
4 |
11 |
0 |
1 |
12 |
7 |
0 |
|
0 |
2 |
14 |
5 |
10 |
12 |
0 |
0 |
|
0 |
0 |
6 |
13 |
10 |
0 |
0 |
0 |
【额外补充】
卷积运算与相关运算
在计算机视觉领域,卷积核、滤波器通常为较小尺寸的矩阵,比如 3 × 3 、5 × 5 等,数字图像是相对较大尺寸的2维(多维)矩阵(张量),图像卷积运算与相关运算的关系如下图所示(图片来自链接),其中 F 为滤波器,X 为图像,O 为结果。
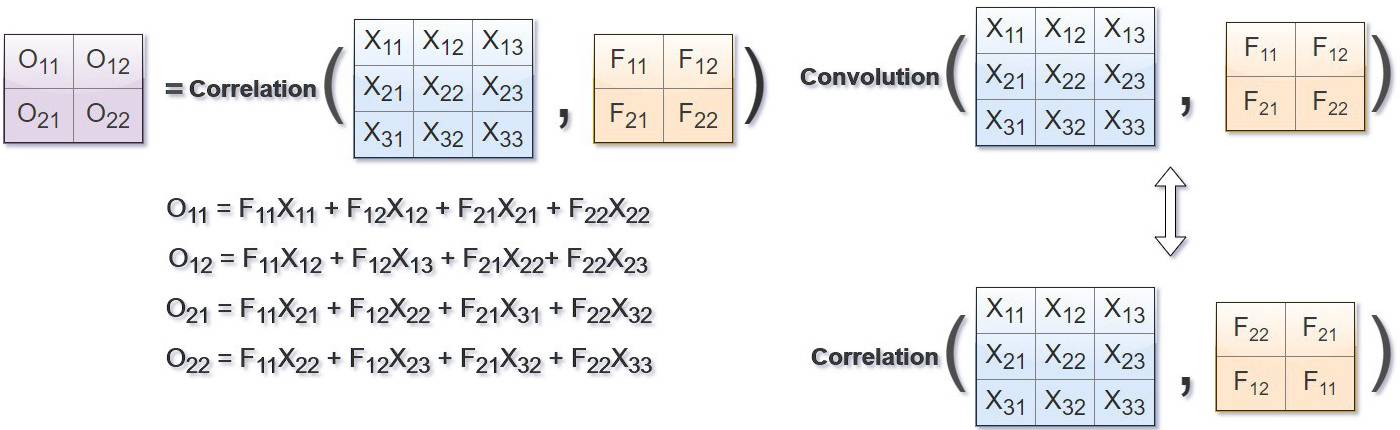
相关是将滤波器在图像上滑动,对应位置相乘求和;
卷积则先将滤波器旋转180度(行列均对称翻转),然后使用旋转后的滤波器进行相关运算。
两者在计算方式上可以等价,有时为了简化,虽然名义上说是“卷积”,但实际实现时是相关。
4.理解卷积如何提取图像特征。
读取一个图像;
1 from PIL import Image 2 import matplotlib.pyplot as plt 3 # %matplotlib inline 4 import numpy as np 5 from scipy.signal import convolve2d 6 import tf.keras.layers.Conv2D 7 8 9 I = Image.open(r'./img/see.jpg') 10 L = I.convert('L') 11 12 cat = np.array(I) # 原图 13 catg = np.array(L) # 灰度图
以下矩阵为卷积核进行卷积操作;
1 k1 = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]]) # 垂直边缘检测 2 k2 = np.array([[1, 1, 1], [0, 0, 0], [-1, -1, -1]]) # 水平边缘检测(转置) 3 k3 = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]]) 4 5 cat1 = convolve2d(catg, k1, boundary='symm', mode='same') 6 cat2 = convolve2d(catg, k2, boundary='symm', mode='same') 7 cat3 = convolve2d(catg, k3, boundary='symm', mode='same')
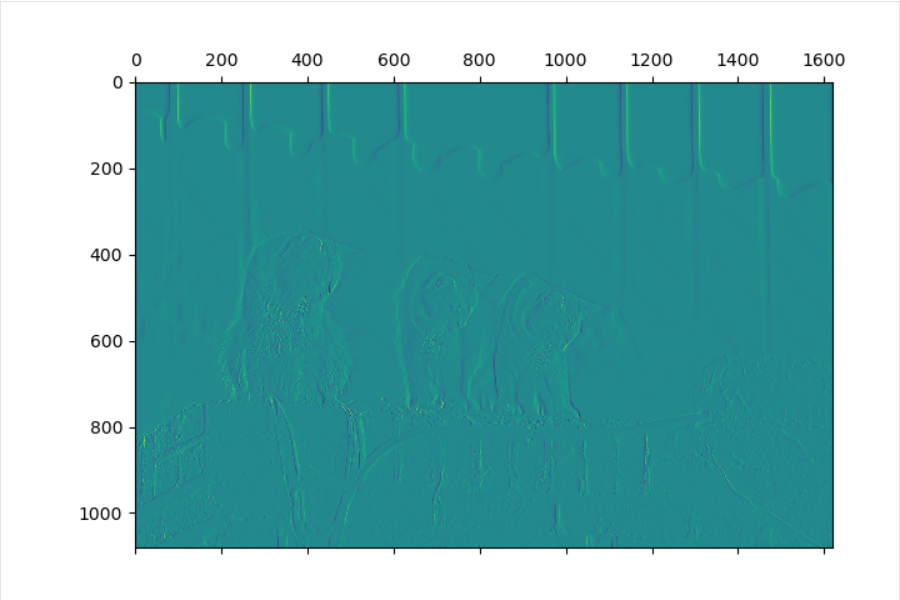
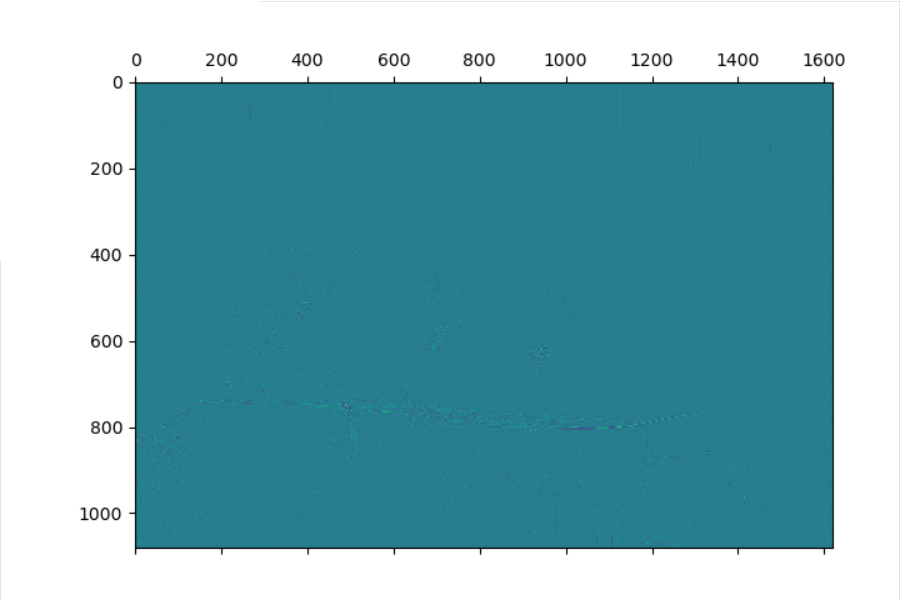
显示卷积之后的图像,观察提取到什么特征。
原图

纵向特征
|
1 |
0 |
-1 |
|
1 |
0 |
-1 |
|
1 |
0 |
-1 |
横向特征
|
1 |
1 |
1 |
|
0 |
0 |
0 |
|
-1 |
-1 |
-1 |

中心特征
|
-1 |
-1 |
-1 |
|
-1 |
8 |
-1 |
|
-1 |
-1 |
-1 |
卷积API
scipy.signal.convolve2d
tf.keras.layers.Conv2D
5. 安装Tensorflow,keras
安装anaconda

在anaconda prompt中运行命令 conda install tensorflow==2.0 进行安装
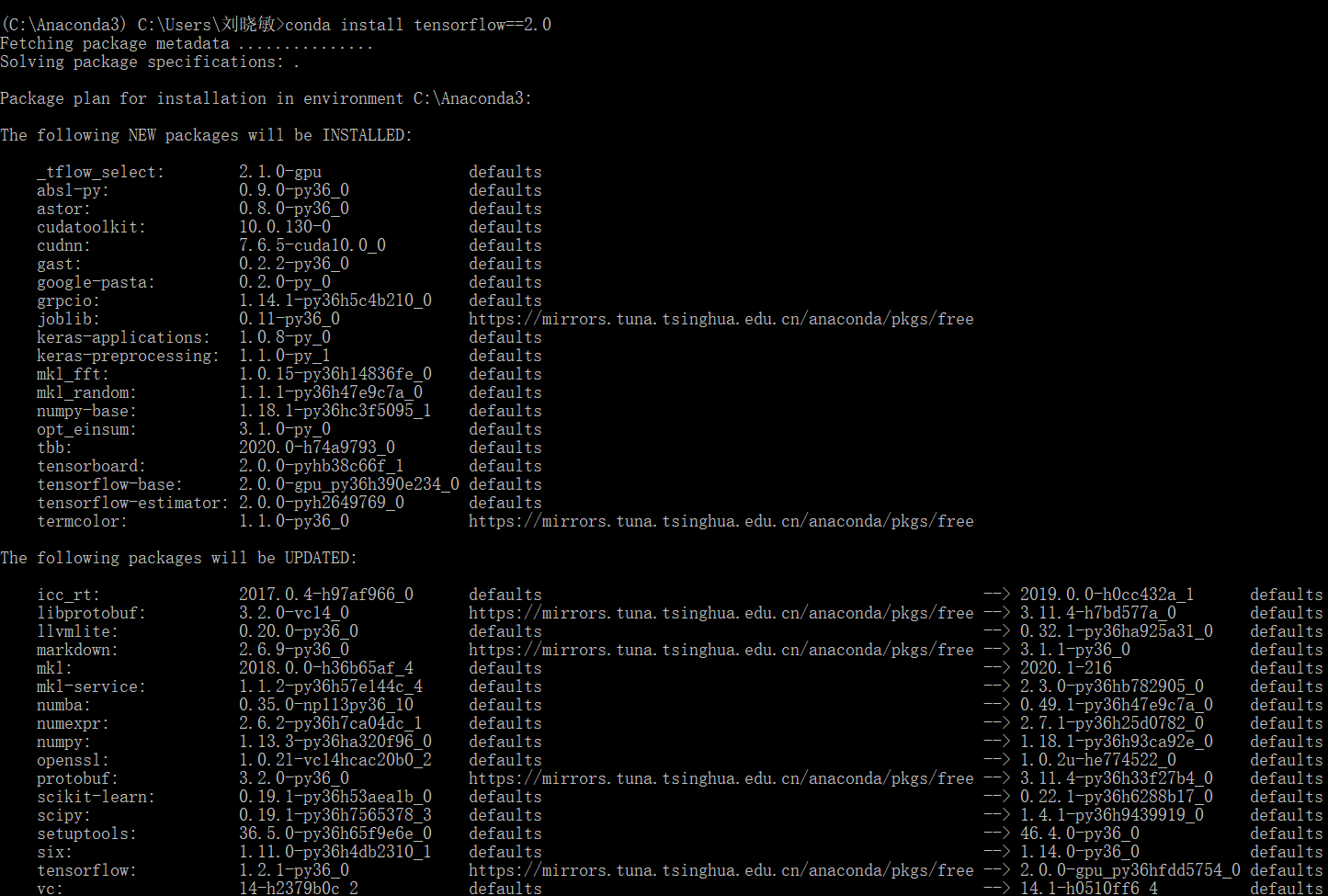
检测安装是否成功

在pycharm导入相关依赖(或者直接在anaconda使用)
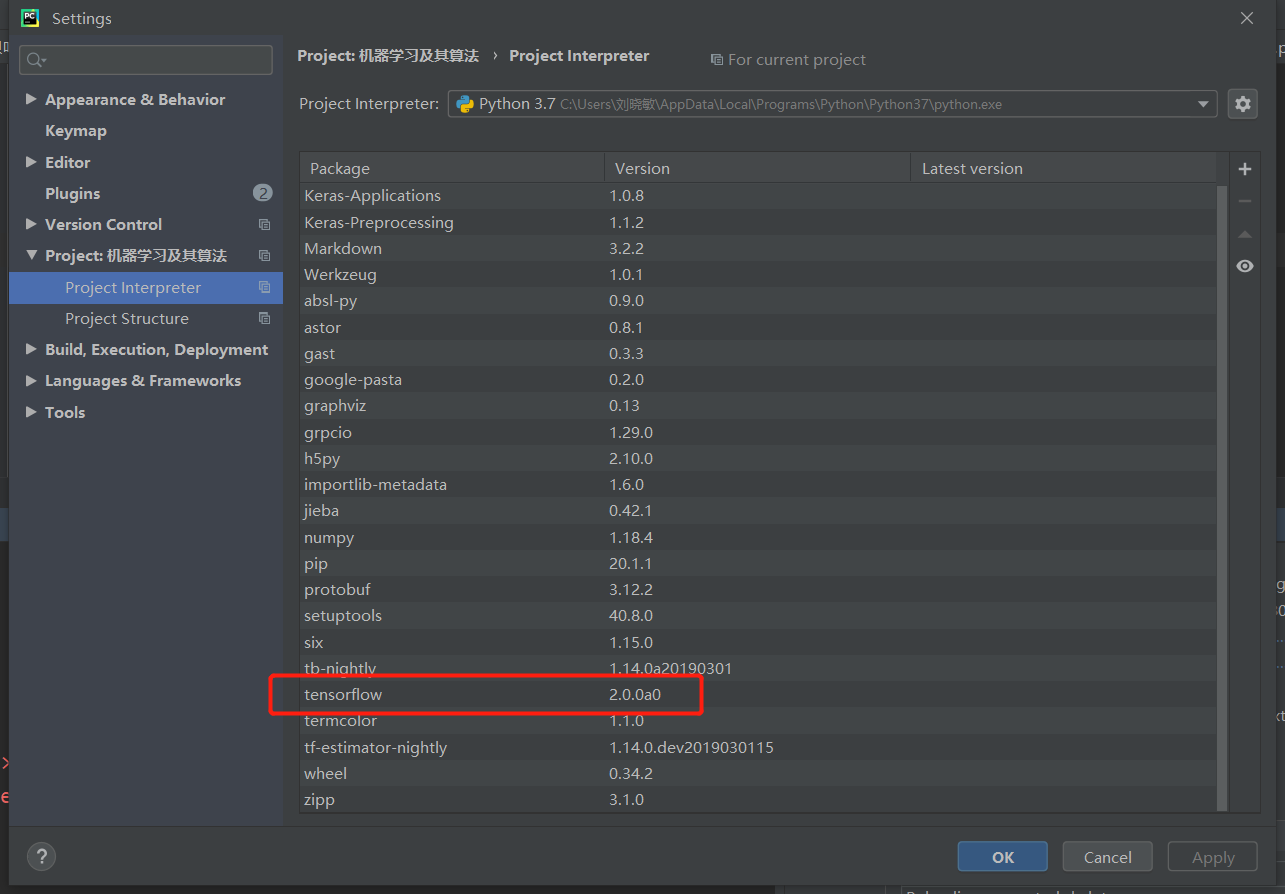
6. 设计手写数字识别模型结构,注意数据维度的变化。
Conv2D相关系数

1 # 导入相关包 2 from tensorflow.keras.models import Sequential 3 from tensorflow.keras.layers import Dense, Dropout, Flatten, Conv2D, MaxPool2D 4 5 # 建立模型 6 model = Sequential() 7 8 # 一层卷积 9 model.add( 10 Conv2D( 11 filters=16, 12 kernel_size=(5, 5), 13 padding='same', # 保证卷积核大小,不够补零 14 input_shape=(28, 28, 1), 15 activation='relu')) 16 # 池化层1 17 model.add(MaxPool2D(pool_size=(2, 2))) 18 19 # 二层卷积 20 model.add( 21 Conv2D( 22 filters=32, 23 kernel_size=(5, 5), # 卷积核的大小 24 padding='same', # 保证卷积核大小,不够补零 25 activation='relu')) 26 # 池化层2 27 model.add(MaxPool2D(pool_size=(2, 2))) 28 model.add(Dropout(0.25)) 29 30 model.add(Flatten()) # 平坦层 31 model.add(Dense(128, activation='relu')) # 全连接层 32 model.add(Dropout(0.25)) 33 model.add(Dense(10, activation='softmax')) # 激活函数
显示每层数据结构的变化过程。model.summary()
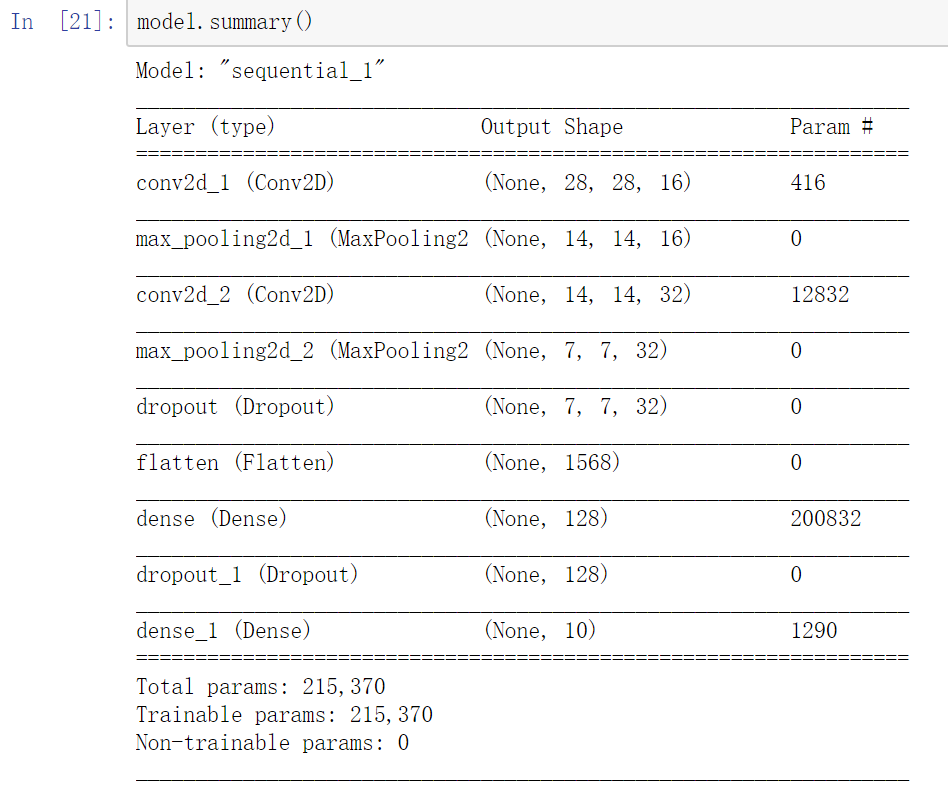
参考:
https://www.jianshu.com/p/afe485aa08ce
https://blog.csdn.net/junjun150013652/article/details/82217571