007整数反转

写在前面，参考的是力扣官网的画解算法

一、java代码

/*
 * @lc app=leetcode.cn id=7 lang=java
 *
 * [7] 整数反转
 */

// @lc code=start
class Solution {
    public int reverse(int x) {

        //定义最后输出的结果为ans
        int ans=0;
        while (x!=0){

            //取个位
            int pop=x%10;
            //判断是否上溢出
            //1、ans>Integer.MAX_VALUE/10，还有pop需要添加
            //2、ans==Integer.MAX_VALUE/10 && pop>7，7是2^31-1的个位数
            if(ans>Integer.MAX_VALUE/10 || (ans==Integer.MAX_VALUE/10 && pop>7)){
                return 0;
            }

            //判断是否下溢出
            //1、ans<Integer.MIN_VALUE/10，还有pop需要添加
            //2、ans==Integer.MIN_VALUE/10 && pop<-8，8是2^31的个位数
            if(ans<Integer.MIN_VALUE/10 || (ans==Integer.MIN_VALUE/10 && pop<-8)){
                return 0;
            }

            //反转输出结果
            ans=ans*10+pop;
            //将数字x的每一位拆开
            x/=10;
        }

        //得到最后的结果
        return ans;

    }
}
// @lc code=end

二、思路分析

2.1溢出

1、通过字符串转换加try catch的方式来解决(效率低)

2、通过数学计算来解决

2.2思路

1、通过循环将数字x的每一位拆开，在计算新值时每一步都判断是否溢出

2、溢出的条件有两个

  （1）大于整数最大值MAX_VALUE

  （2）小于整数最小值MIN_VALUE

3、设当前计算结果为ans；下一位为pop

4、从ans*10+pop>MAX_VALUE这个溢出条件来看

  （1）当出现ans>MAX_VALUE/10且还有pop需要添加时，则一定溢出

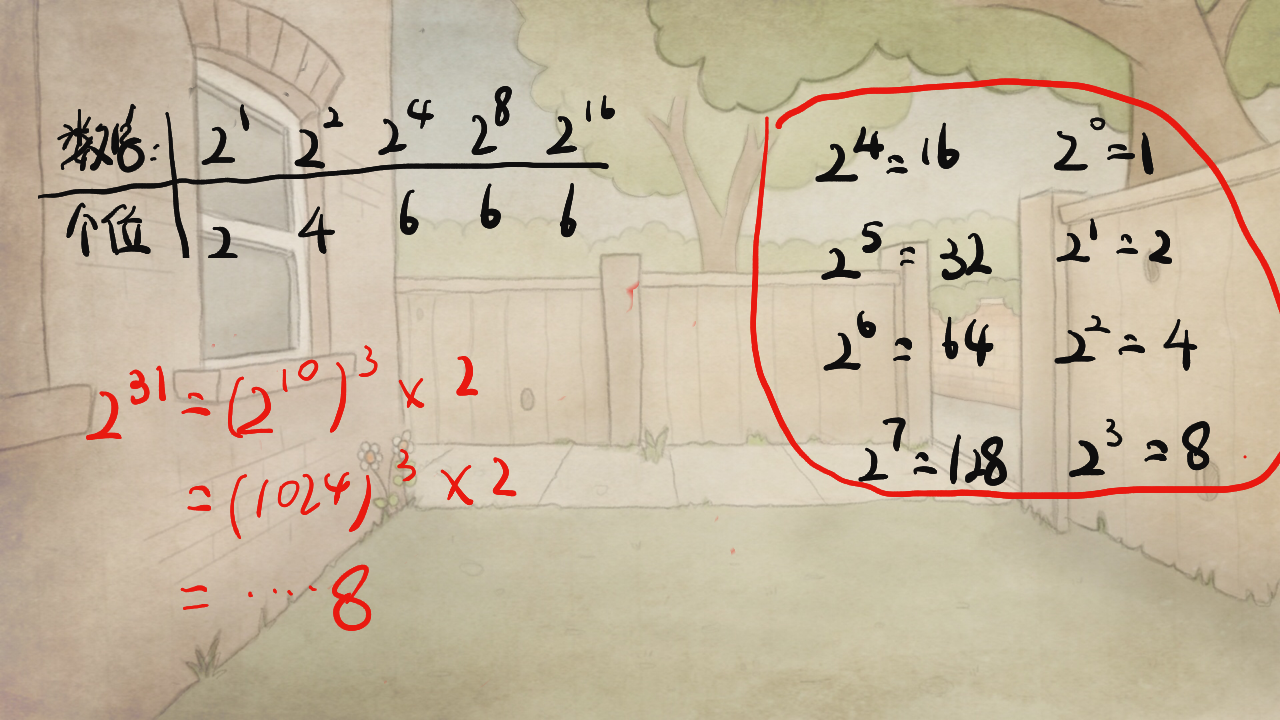
  （2）当出现ans=MAX_VALUE/10且pop>7时，则一定溢出，7是2^31-1的个位数

5、从ans*10+pop<MIN_VALUE这个溢出条件来看

  （1）当出现ans<MIN_VALUE/10且还有pop需要添加时，则一定溢出

  （2）当出现ans=MIN_VALUE/10且pop<-8时，则一定溢出，8是2^31的个位数

三、画图举例

拆解

3.1

3.2

3.3