学号20162320 《程序设计与数据结构》第8周学习总结
教材学习内容总结
一、堆
堆是一棵完全二叉树,其中每个元素大于等于其所有子结点的值。准确的说这是最大堆(maxheap)的定义,堆还可以是最小堆(minheap),即每个元素都小于等于它的孩子
堆有三种基本操作:
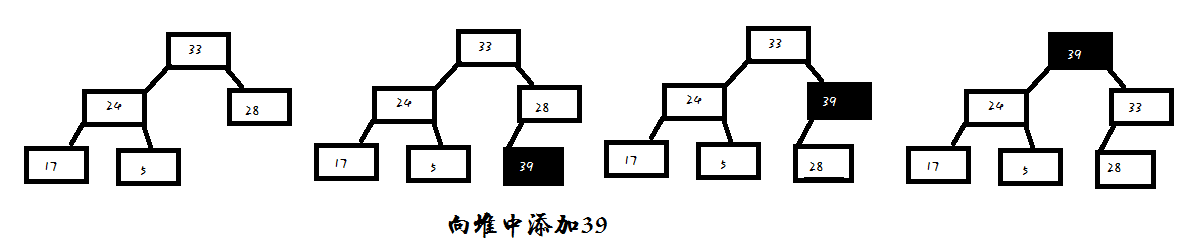
- 1.向堆中添加一个新元素
策略:将元素添加为新的叶结点,同时保持树是完全树,然后将该元素向根的方向移动,与它的父结点对换,直到其中的元素大小关系满足要求为止。
- 2.找到最大元素
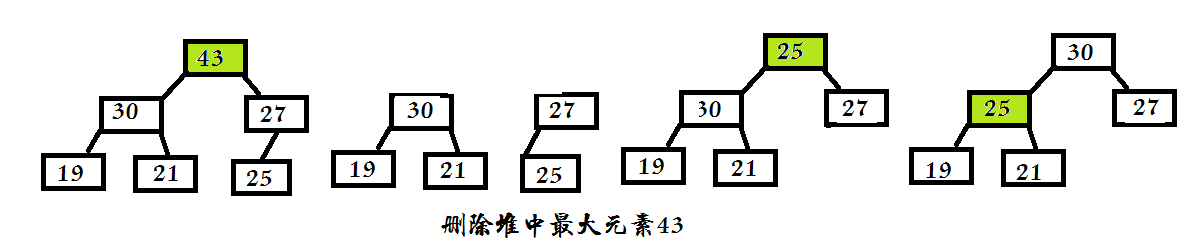
- 3.删除最大元素
策略:由堆的特性得知,最大元素在根上,所以删除最大元素就是要删除根结点,然后将余下的两个分开的子树重新构造为堆。
利用最后的叶结点来取代根,然后将其向下移动到合适的位置。
二、堆的排序
堆排序是先将一组元素一项项地插入到堆中,然后一次删除一个,因为元素最先从堆中删除(在最大堆中),从堆中得到的元素序列将是有序序列,而且是降序的,类似地,一个最小堆可用来得到升序的排序结果。
算法思路:每次将堆的堆顶记录输出;同时调整剩余的记录,使他们重新排成一个堆。重复以上过程。
1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆,此堆为初始的无须区;
2)将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n];
3)由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。(转)
public int[] heapSort(int[] array){
array = buildMaxHeap(array);
for(int i=array.length-1;i>1;i--){
int temp = array[0];
array[0] = array[i];
array[i] = temp;
adjustDownToUp(array, 0,i);
}
return array;
}
代码实现思路:首先初始建堆,array[0]为第一趟值最大的元素, 将堆顶元素和堆低元素交换,即得到当前最大元素正确的排序位置,最后将剩余的元素整理成堆。
三、优先队列
优先队列(priority queue)是一个服从两个有序规则的集合。首先,具有更高优先级的项排在前面,其次,具有相同优先级的项按先进先出的规则排序。
优先队列不是FIFO队列,它根据优先级排序元素,而不是根据它们进入队列的次序排序。
可用多个队列来实现优先队列,具有相同优先级的项保存在一个队列中。对于这个问题的更好的解决方案是使用堆。如果按优先级进行排序,就能看出优先队列和堆之间存在的自然关系,但要注意的是,具有相同优先级的项采用先进先出的原则,并没有自动应用到堆中。
教材学习中的问题和解决过程
- 问题1: 一个有n个结点的堆的插入和删除操作,时间复杂度是多少?为什么?
解答:假设该二叉树总共有x层,当该二叉树为满二叉树的时候,插入和删除耗费的时间是最长的,那么则有:
2^x - 1 = n;在最坏的情况下,我们插入一个元素是从第一层遍历到第n层,那么进行的操作次数是树的深度,而树的深度x = log(2)(n+1)(表示以2为底,以n+1为真数的对数),忽略常数,那么我们就求得插入时的最坏时间复杂度则为O(logn)级别。 - 问题2:堆与二叉查找树的区别是什么?
解答:具有n个结点的二叉查找树和堆都是约束了元素之间关系的二叉树。
(1)二叉查找树的结点大于它的左子结点,并小于等于它的右子结点,而(最大)堆中的结点大于等于它的两个子结点。
(2)二叉排序树的深度取决于给定集合的初始排列顺序,在最优情况的深度为log n(表示以2为底的对数),最坏情况下其深度为n;而堆的深度是为堆所对应的完全二叉树的深度log n 。
(3)二叉排序树是为了实现动态查找而设计的数据结构,它是面向查找操作的,在二叉排序树中查找一个结点的平均时间复杂度是O(log n);堆是为了实现排序而设计的一种数据结构,它不是面向查找操作的,因而在堆中查找一个结点需要进行遍历,其平均时间复杂度是O(n)。
代码学习中的问题及解决
- 问题1:完成作业PP18.1,实现程序设计项目中的
getMax()方法
解答:
HeapNode<T> node = new HeapNode<T>(element);
HeapNode<T> newParent = null;
if (root == null) root = node;
else {
newParent = ((HeapNode<T>)root).getParentAdd(last);
if (newParent.left == null)
newParent.setLeft(node);
else
newParent.setRight(node);
}
node.setParent(newParent);
last = node;
((HeapNode<T>)root).heapifyAdd(last);
}
在LinkedMaxHeap类中已经给出了add的方法,可以知道add方法中引用HeapNode中排序的方法,将元素与其的左右子结点进行比较,若子结点大于父结点,则交换二者。所以建立测试用例中添加大小顺序不同的数入堆中就已经排好序,已知最大堆中根结点是最大元素,所以getMax()可以直接返回根结点。return root.getElement();
- 问题2:完成PP18.5,实现堆排序算法
public static class HeapSort {
private int[] buildMaxHeap(int[] array) {
//从最后一个节点array.length-1的父节点(array.length-1-1)/2开始,直到根节点0,反复调整堆
for (int i = (array.length - 2) / 2; i >= 0; i--) {
adjustDownToUp(array, i, array.length);
}
return array;
}
private void adjustDownToUp(int[] array, int k, int length) {
int temp = array[k];
for (int i = 2 * k + 1; i < length - 1; i = 2 * i + 1) {
if (i < length && array[i] < array[i + 1]) {
i++;
}
if (temp >= array[i]) {
break;
} else {
array[k] = array[i];
k = i;
}
}
array[k] = temp;
}
public int[] heapSort(int[] array) {
array = buildMaxHeap(array);
for (int i = array.length - 1; i > 1; i--) {
int temp = array[0];
array[0] = array[i];
array[i] = temp;
adjustDownToUp(array, 0, i);
}
return array;
}
public void toString(int[] array) {
for (int i : array) {
System.out.print(i + " ");
}
}
}
解答:首先初始建立最大堆,array[0]为第一趟值最大的元素, 将堆顶元素和堆低元素交换,即得到当前最大元素正确的排序位置,最后将剩余的元素整理成堆。
- 1)将存放在array[0,...,n-1]中的n个元素建成初始堆;
- 2)将堆顶元素与堆底元素进行交换,则序列的最大值即已放到正确的位置;
- 3)但此时堆被破坏,将堆顶元素向下调整使其继续保持大根堆的性质,再重复第23步,直到堆中仅剩下一个元素为止。
代码托管
(statistics.sh脚本的运行结果截图)
上周考试错题总结
- 错题1:
Which of the following best describes a balanced tree?
A .A balanced trees has all nodes at exactly the same level.
B .A balanced tree has no nodes at exactly the same level.
C .A balanced tree has half of the nodes at one level and half the nodes at another level.
D .A balanced tree has all of the nodes within one level of each other.
E .none of the above correctly describe a balanced tree.
解答:D,我选的是E,我认为ABCD四个选项描述平衡树的概念都不完整或片面。比如说答案A,尽管树的节点在同一层次上是平衡的,但并不是所有的平衡树都有这个属性。所有A错误。相对其他选项只有D是正确定义了平衡树。
- 错题2:
A .true
B .false
解答:B,这个题目答案应该是给错了,因为答案给的是在后序遍历中根是最后访问的一个元素,这应该和A选项符合。
结对及互评
点评过的同学博客和代码
- 本周结对学习情况
其他(感悟、思考等,可选)
You have to fight to reach your dream. You have to sacrifice and work hard for it. 为了实现梦想,你必须奋斗;你必须做出牺牲,必须为之努力。调整心态,继续前行,未来加油。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 188 | 1/1 | 25 | 算法分析 |
| 第二周 | 70/258 | 1/2 | 15/40 | 《构建之法》7-9章 |
| 第三周 | 474/732 | 1/3 | 20/60 | 查找和排序 |
| 第四五六周 | 1313/2045 | 4/7 | 12/72 | 栈和队列 |
| 第七周 | 890/2935 | 1/8 | 14/86 | 树 |
| 第八周 | 913/3848 | 1/9 | 20/106 | 二叉查找树 |
| 第九周 | 890/3738 | 1/10 | 13/119 | 堆 |
| 第十周 |
- 计划学习时间: 20+小时
- 实际学习时间: 25小时
(有空多看看现代软件工程 课件 软件工程师能力自我评价表)