一.函数式编程
1.函数与闭包
函数式编程vc函数指针
- 函数是一等公民:参数,边临,返回值都可以是函数
- 高阶函数
- 函数->闭包
"正统"函数式编程
- 不可变性:不能有状态,只有常量和函数
- 函数只能有一个参数

package main
import "fmt"
func adder() func(int) int {
sum := 0
return func(v int) int {
sum += v
return sum
}
}
func main() {
a := adder()
for i := 0; i < 10; i++ {
fmt.Printf("0+1+...%d=%d\n",i,a(i))
}
}
package main
import "fmt"
func adder() func(int) int {
sum := 0
return func(v int) int {
sum += v
return sum
}
}
/**
正统
*/
type iAdder func(int) (int, iAdder)
func adder2(base int) iAdder {
return func(v int) (int, iAdder) {
return base + v, adder2(base + v)
}
}
func main() {
a := adder2(0)
for i := 0; i < 9; i++ {
var s int
s, a = a(i)
fmt.Printf("0+1+...%d=%d\n", i, s)
}
}
2.闭包的应用
- 更为自然,不需要修饰如何访问自由变量
- 没有lambda表达式,但是有匿名函数
扩展:
二叉树遍历(前序、中序、后序、层次遍历、深度优先、广度优先)
二叉树是一种非常重要的数据结构,很多其它数据结构都是基于二叉树的基础演变而来的。对于二叉树,有深度遍历和广度遍历,深度遍历有前序、中序以及后序三种遍历方法,广度遍历即我们平常所说的层次遍历。因为树的定义本身就是递归定义,因此采用递归的方法去实现树的三种遍历不仅容易理解而且代码很简洁,而对于广度遍历来说,需要其他数据结构的支撑,比如堆了。所以,对于一段代码来说,可读性有时候要比代码本身的效率要重要的多。
四种主要的遍历思想为:
前序遍历:根结点 ---> 左子树 ---> 右子树
中序遍历:左子树---> 根结点 ---> 右子树
后序遍历:左子树 ---> 右子树 ---> 根结点
层次遍历:只需按层次遍历即可
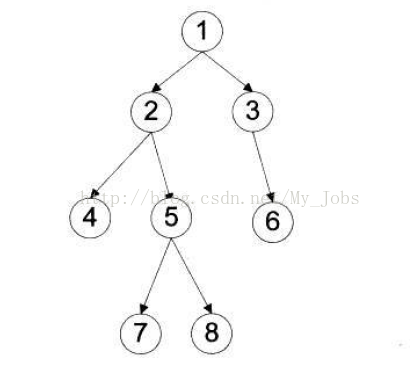
例如,求下面二叉树的各种遍历
前序遍历:1 2 4 5 7 8 3 6
中序遍历:4 2 7 5 8 1 3 6
后序遍历:4 7 8 5 2 6 3 1
层次遍历:1 2 3 4 5 6 7 8