PriorityQueue详解

美人如斯！好好看文章！

前言

java中关于Queue队列的实现繁多（关于Queue可以移步至我的另一篇文章：《Queue介绍》），每种实现根据自身的特性都有相应的应用场景。这里我们就来聊聊Queue的直接实现PriorityQueue队列，主要从以下几个方面看看：

• PriorityQueue是什么
• PriorityQueue特性
• PriorityQueue实现原理

一.PriorityQueue

顾名思义：PriorityQueue是和优先级有关系的一种队列。的确，它是优先队列，这里的优先是指：根据某种规则将队列元素进行排序，每次出队时总是取出排序中的最大或者最小元素，这样的特性决定优先队列不完全遵循FIFO规则，其中排序规则可以决策元素的优先级。
这里通过一个简单的例子来看一看PriorityQueue的入队和出队情况：

public void addTest() {

    Queue<Integer> random = new PriorityQueue<>();
    System.out.println("输入：" + "2,1,3,");
    random.add(2); random.add(1); random.add(3);
    System.out.print("输出：" );
    int rs = random.size();
    for (int i = 0; i < rs; i++) {
       System.out.print(random.remove() + ",");
    }
}

根据FIFO算法，上述结果应该是：

输入：2,1,3,  
输出：2,1,3,

但是实际输出：

输入：2,1,3,
输出：1,2,3,

可以看出，优先队列按照自然顺序对元素进行排序。

二.特性

PriorityQueue具有以下特性：

• 队列元素根据自然排序或者根据具体的比较器排序
• 实例化时若未指定初始容量，默认容量为11
• 自动扩容。如果容量小于64，两倍增长扩容；否则增长50%
• 无边界容器
• 迭代器不具有以特定顺序访问队列元素
• 不支持null元素
• 非线程安全
• 支持被序列化
• 入队出队的时间复杂度O(log(n))

三.原理

1. 存储结构

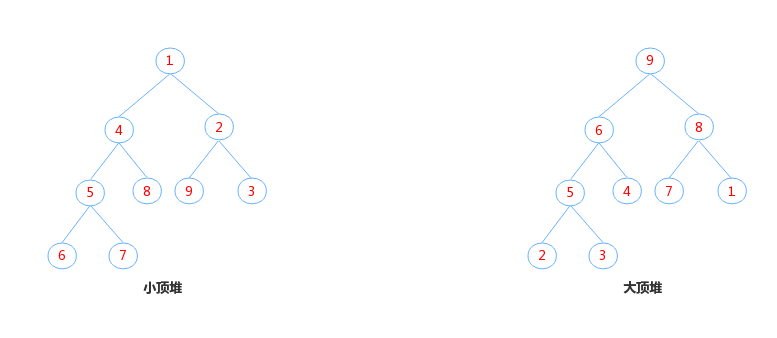
在介绍PriorityQueue之前，先来温习下一种基本的数据结构——堆，定义如下：

• 是一颗完全二叉树；
• 其中任意节点的都不大于（不小于）左节点的值和右节点的值；

因为是完全二叉树，所以满足val(n) > val(2n+1) && val(n) > val(2(n+1))或者val(n) < val(2n+1) && val(n) < val(2(n+1))。正是节点之间存在这样线性关系，堆的存储可以使用线性数组实现。其中不小于时，是大顶堆，不大于时，是小顶堆。如下图:

关于堆的具体详情，这里就不再赘述，这里主要以介绍PriorityQueue为主。PriorityQueue是基于堆，所以建议读者在了解其之前，先熟悉堆的数据结构，可移步至基本数据结构——堆(Heap)的基本概念及其操作和图解排序算法(三)之堆排序。

PriorityQueue本质正是小顶堆，每次出队时，总是获取值最小的元素。其内部的存储使用线性数组，可以看下代码：

/**
 * Priority queue represented as a balanced binary heap: the two
 * children of queue[n] are queue[2*n+1] and queue[2*(n+1)].  The
 * priority queue is ordered by comparator, or by the elements'
 * natural ordering, if comparator is null: For each node n in the
 * heap and each descendant d of n, n <= d.  The element with the
 * lowest value is in queue[0], assuming the queue is nonempty.
 */
transient Object[] queue; // non-private to simplify nested class access

从以上java doc中可以看出，优先队列被当做为平衡二叉堆，即n下标的元素的两个孩子分别是2n+1和2n+2下标的元素。优先队列元素按照比较器comparator排序，如果比较器为空，按照元素的自然顺序排序。队列中的元素最小值是下标为0的元素，即是小顶堆！

优先队列持有int类型值：

/**
 * The number of elements in the priority queue.
 */
private int size = 0;

用来记录当前队列的元素个数，当入队时，size加1，当出队时size减1。
size()方法将通过返回size值来实现统计当前队列的元素个数。

优先队列中有个比较器对象：

/**
 * The comparator, or null if priority queue uses elements'
 * natural ordering.
 */
private final Comparator<? super E> comparator;

该比较器用于在入队或者出队时，比较队列元素，重新排序，构造小顶堆。
可以在实例化优先队列对象时通过指定构造函数中比较器参数进行赋值，这个在后面将会详解。

还持有一个int类型值：

/**
 * The number of times this priority queue has been
 * <i>structurally modified</i>.  See AbstractList for gory details.
 */
transient int modCount = 0; // non-private to simplify nested class access

该变量用于记录优先队列的修改次数，以在并发情况下访问时，实现fast-fail。

2. 构造函数

优先队列PriorityQueue共有多种构造函数，其中以以下为主：
1）无参构造函数，初始化一个容量为11的且以自然顺序排序元素的优先队列

public PriorityQueue() {
    this(DEFAULT_INITIAL_CAPACITY, null);
}

2）初始化指定大小的容量的优先队列，且以自然顺序排列元素

public PriorityQueue(int initialCapacity) {
    this(initialCapacity, null);
}

3）初始化指定的比较器的优先队列

public PriorityQueue(Comparator<? super E> comparator) {
    this(DEFAULT_INITIAL_CAPACITY, comparator);
}

4）初始化指定大小和比较器的优先队列

public PriorityQueue(int initialCapacity,
                     Comparator<? super E> comparator) {
    // Note: This restriction of at least one is not actually needed,
    // but continues for 1.5 compatibility
    if (initialCapacity < 1)
        throw new IllegalArgumentException();
    this.queue = new Object[initialCapacity];
    this.comparator = comparator;
}

如果指定初始化容量小于1，将抛出IllegalArgumentException。

3. 重要接口实现

优先队列是队列中的一种实现，也不外乎就是队列的插入、移除、检查的几种行为。下面就让我们以源码的方式来看看优先队列中的这几种行为的具体实现。

1）add方法

/**
 * Inserts the specified element into this priority queue.
 *
 * @return {@code true} (as specified by {@link Collection#add})
 * @throws ClassCastException if the specified element cannot be
 *         compared with elements currently in this priority queue
 *         according to the priority queue's ordering
 * @throws NullPointerException if the specified element is null
 */
public boolean add(E e) {
    return offer(e);
}

add方法实际是调用offer实现，且从java doc中可以看出，不支持插入null。如果插入的元素不能与队列中的元素比较大小，则会抛出ClassCastException异常。
下面继续看看offer内部实现，在看之前，先来看看小顶堆的构造过程：

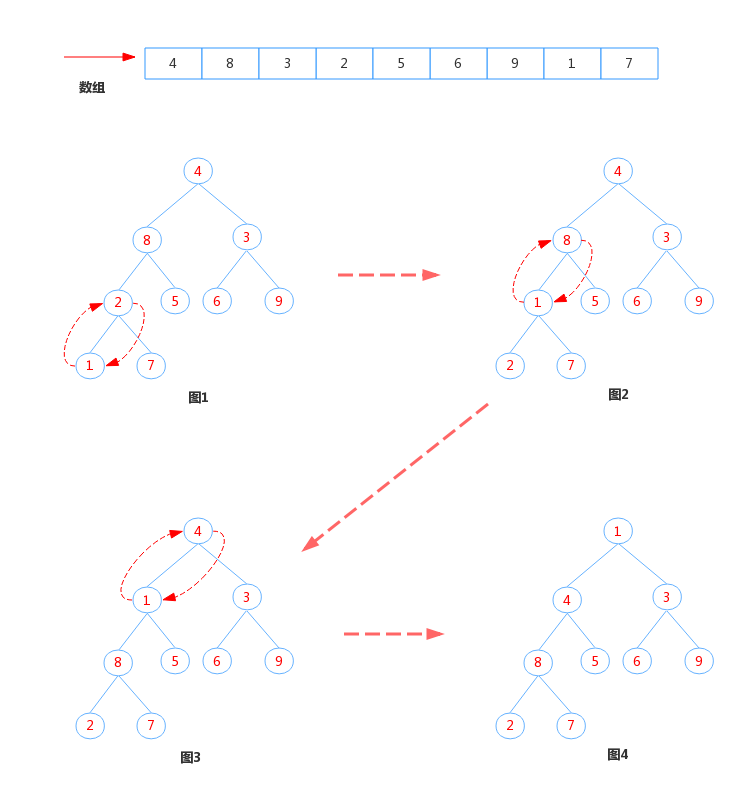
1. 将数组按顺序构造成一颗完全二叉树
2. 从左至右，从下往上，将具有子节点的节点的值与其左右子节点值比较，交换最小的为父节点，直到将最小的节点交换到根节点位置

以上的过程称作为：上浮(sitUp)，通过上浮操作就能找出最小值，重复上浮操作的过程，就能构造出小顶堆。

2）offer方法

/**
 * Inserts the specified element into this priority queue.
 *
 * @return {@code true} (as specified by {@link Queue#offer})
 * @throws ClassCastException if the specified element cannot be
 *         compared with elements currently in this priority queue
 *         according to the priority queue's ordering
 * @throws NullPointerException if the specified element is null
 */
public boolean offer(E e) {
    if (e == null)
        throw new NullPointerException();
    modCount++;
    int i = size;
    if (i >= queue.length)
        grow(i + 1);
    size = i + 1;
    if (i == 0)
        queue[0] = e;
    else
        siftUp(i, e);
    return true;
}

首先判断插入元素e是否为null，如果是，则抛出啊NullPointerException。然后记录一次修改，modCount加1。
再判断队列容量是否足够，如果不足则进行扩容操作，否则将元素个数加1。
这里继续往下看如何插入数组中，扩容操作后面介绍。
在插入之前，先if判断队列中是否有元素，如果无，则直接将元素插入数组的第一个位置，返回true；如果有，则进行上浮，优先队列中通过sitUp方法实现，下面继续来看看sitUp方法：

/**
 * Inserts item x at position k, maintaining heap invariant by
 * promoting x up the tree until it is greater than or equal to
 * its parent, or is the root.
 *
 * To simplify and speed up coercions and comparisons. the
 * Comparable and Comparator versions are separated into different
 * methods that are otherwise identical. (Similarly for siftDown.)
 *
 * @param k the position to fill
 * @param x the item to insert
 */
private void siftUp(int k, E x) {
    if (comparator != null)
        siftUpUsingComparator(k, x);
    else
        siftUpComparable(k, x);
}

该方法有两个参数，k标识元素插入的位置，x表示待插入元素。插入一个元素肯定是需要重新进行上浮，将最小值保持在根节点处。api定义非常合理，插入动作肯定需要两个要素：位置和元素！
首先判断当前队列是否有比较器，如果有则就是用比较器比较元素进行上浮，否则使用元素的自然顺序比较进行上浮。
两个实现只是元素比较上的差异，整个上浮的算法流程是一样的，这里只详细的分析下使用自然顺序比较的方式：

private void siftUpComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>) x;
    while (k > 0) {
        int parent = (k - 1) >>> 1;   //计算插入位置的父节点的数组下标
        Object e = queue[parent];
        if (key.compareTo((E) e) >= 0) //比较父节点与待插入的大小
            break;   //如果待插入较大，循环中断
        queue[k] = e; //将父节点值下沉
        k = parent; //将父节点下标赋值给k，继续循环判断
    }
    queue[k] = key; 
}

根据堆的父节点与左右孩子节点的线性关系：

• left_Children = 2n +1
• right_Children = 2(n+1)

首先计算出插入位置的的父节点parent，然后将parent的值与待插入元素比较。如果待插入元素较大，则不需要上浮，循环结束，直接将x插入k位置；如果较小，则将parent的值下沉至k位置， 再比较父节点的父节点值与待插入元素，如此重复，直到k等于0或者带插入元素比其中节点值大，循环break出来。

3）remove方法

该方法是移除并返回优先队列的队头元素。PriorityQueue中队头即小顶堆的根节点，队尾即最后一个叶子节点的下一位置。PriorityQueue的remove方法是继承AbstractQueue的实现：

/**
 * Retrieves and removes the head of this queue.  This method differs
 * from {@link #poll poll} only in that it throws an exception if this
 * queue is empty.
 *
 * <p>This implementation returns the result of <tt>poll</tt>
 * unless the queue is empty.
 *
 * @return the head of this queue
 * @throws NoSuchElementException if this queue is empty
 */
public E remove() {
    E x = poll();
    if (x != null)
        return x;
    else
        throw new NoSuchElementException();
}

首先看下java doc描述，该方法是移除并获得队头元素，与poll方法不一样，如果队列为空则抛出NoSuchElementException
remove中直接调用poll，如果该元素非空则直接返回，否则抛出异常！

3）poll方法

public E poll() {
    if (size == 0)
        return null;
    int s = --size;
    modCount++;
    E result = (E) queue[0];
    E x = (E) queue[s];
    queue[s] = null;
    if (s != 0)
        siftDown(0, x);
    return result;
}

首先判断队列是否为空，如果空，则返回null。然后队列大小减1，记录一次修改次数。
取出队头元素和队尾元素，将队尾置空移除。
判断此时队列是否为空，若空，则返回队头元素，否则执行下沉操作，这里先通过图解的方式来直观的感受下下沉操作的过程，再进一步分析代码。下沉过程：

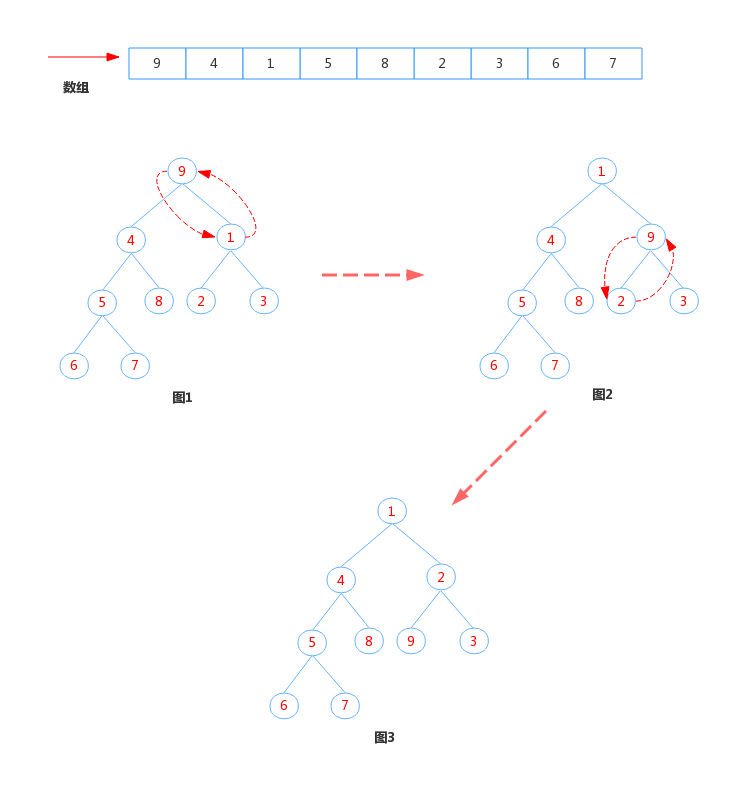
从根节点开始，从上往下，将父节点和左右子节点比较，将较小的子节点和父节点交换，将被交换的子节点重新作为父节点再与其子节点比较并交换，直到变成叶子节点或者比左右子节点都小时结束。这样就重新构成了小顶堆。
下面再来看下下沉过程的实现：

/**
 * Inserts item x at position k, maintaining heap invariant by
 * demoting x down the tree repeatedly until it is less than or
 * equal to its children or is a leaf.
 *
 * @param k the position to fill
 * @param x the item to insert
 */
private void siftDown(int k, E x) {
    if (comparator != null)
        siftDownUsingComparator(k, x);
    else
        siftDownComparable(k, x);
}

private void siftDownComparable(int k, E x) {
    Comparable<? super E> key = (Comparable<? super E>)x;
    int half = size >>> 1;        // loop while a non-leaf
    while (k < half) {
        int child = (k << 1) + 1; // assume left child is least
        Object c = queue[child];
        int right = child + 1;
        if (right < size &&
            ((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
            c = queue[child = right];
        if (key.compareTo((E) c) <= 0)
            break;
        queue[k] = c;
        k = child;
    }
    queue[k] = key;
}

和上浮实现类似，比较器为空时使用自然顺序比较。这里主要分析自然顺序比较的下沉过程。
首先根据队列元素个数计算堆的深度，判断下沉元素位置与深度大小关系，如果比深度值小，可认为下沉元素是非叶子节点。然后根据下沉元素k位置计算出左子节点和右子节点，然后比较，找出较小值给临时变量c，再将待插入元素x与c比较，如果待插入元素比左右子节点都小，则结束循环。否则将子节点值赋值给k位置，并将该子节点的位置作为新的下沉位置，继续循环。

3）element方法和peek方法

/**
 * Retrieves, but does not remove, the head of this queue.  This method
 * differs from {@link #peek peek} only in that it throws an exception if
 * this queue is empty.
 *
 * <p>This implementation returns the result of <tt>peek</tt>
 * unless the queue is empty.
 *
 * @return the head of this queue
 * @throws NoSuchElementException if this queue is empty
 */
public E element() {
    E x = peek();
    if (x != null)
        return x;
    else
        throw new NoSuchElementException();
}

PriorityQueue的element是继承自AbstractQueue，调用peek，然后判断元素是否为空，若不为空，则直接返回元素。否则抛出NoSuchElementException。

public E peek() {
    if (size == 0)
        return null;
    return (E) queue[0];
}

如果队列为空，则返回null，否则返回队头元素，这里并不移除。

PriorityQueue还有其他的一些操作，比如根据一个现有集合初始化优先队列等，这里不再赘述，感兴趣的读者可以自行阅读源码和编写测试代码学习。