连续碰到几个与卡塔兰数相关的题,忍不住写一篇博客。
递推公式的几种表达:
1、h(0)=h(1)=1;h(n)=h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
2、h(n)=h(n-1)*(4*n-2)/(n+1);
3、h(n)=c(2n,n)/(n+1);
4、h(n)=c(2n,n)-c(2n,n-1);
卡塔兰数抽象成图像模型:
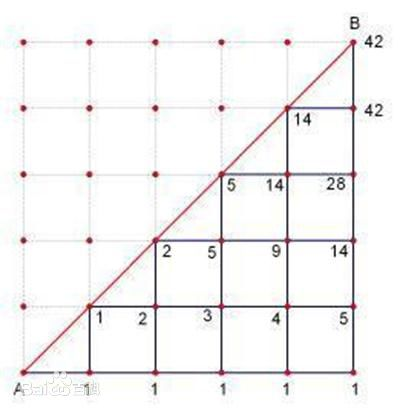
意思是从原点向上走到(n,n),只能向上和向右,且y<=x始终成立共有多少种走法。
抽象成数学模型就是:n个1和n个0组成排列,要求在组成的排列中,在任意的前k个字符中,1的个数不能少于0的个数。
卡塔兰数的应用:
应用
括号化
矩阵连乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,试问有几种括号化的方案?(h(n)种)[4]
因为将前n个数括号化,括号的个数必然不超过n/2个,符合卡塔兰数的性质
出栈次序
常规分析
首先,我们设f(n)=序列个数为n的出栈序列种数。(我们假定,最后出栈的元素为k,显然,k取不同值时的情况是相互独立的,也就是求出每种k最后出栈的情况数后可用加法原则,由于k最后出栈,因此,在k入栈之前,比k小的值均出栈,此处情况有f(k-1)种,而之后比k大的值入栈,且都在k之前出栈,因此有f(n-k)种方式,由于比k小和比k大的值入栈出栈情况是相互独立的,此处可用乘法原则,f(n-k)*f(k-1)种,求和便是Catalan递归式。)
首次出空之前第一个出栈的序数k将1~n的序列分成两个序列,其中一个是1~k-1,序列个数为k-1,另外一个是k+1~n,序列个数是n-k。
此时,我们若把k视为确定一个序数,那么根据乘法原理,f(n)的问题就等价于——序列个数为k-1的出栈序列种数乘以序列个数为n - k的出栈序列种数,即选择k这个序数的f(n)=f(k-1)×f(n-k)。而k可以选1到n,所以再根据加法原理,将k取不同值的序列种数相加,得到的总序列种数为:f(n)=f(0)f(n-1)+f(1)f(n-2)+……+f(n-1)f(0)。
看到此处,再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n)= C(2n,n)/(n+1)= c(2n,n)-c(2n,n-1)(n=0,1,2,……)。
最后,令f(0)=1,f(1)=1。
非常规分析
对于每一个数来说,必须进栈一次、出栈一次。我们把进栈设为状态‘1’,出栈设为状态‘0’。n个数的所有状态对应n个1和n个0组成的2n位二进制数。由于等待入栈的操作数按照1‥n的顺序排列、入栈的操作数b大于等于出栈的操作数a(a≤b),因此输出序列的总数目=由左而右扫描由n个1和n个0组成的2n位二进制数,1的累计数不小于0的累计数的方案种数。
在2n位二进制数中填入n个1的方案数为c(2n,n),不填1的其余n位自动填0。从中减去不符合要求(由左而右扫描,0的累计数大于1的累计数)的方案数即为所求。
不符合要求的数的特征是由左而右扫描时,必然在某一奇数位2m+1位上首先出现m+1个0的累计数和m个1的累计数,此后的2(n-m)-1位上有n-m个 1和n-m-1个0。如若把后面这2(n-m)-1位上的0和1互换,使之成为n-m个0和n-m-1个1,结果得1个由n+1个0和n-1个1组成的2n位数,即一个不合要求的数对应于一个由n+1个0和n-1个1组成的排列。
反过来,任何一个由n+1个0和n-1个1组成的2n位二进制数,由于0的个数多2个,2n为偶数,故必在某一个奇数位上出现0的累计数超过1的累计数。同样在后面部分0和1互换,使之成为由n个0和n个1组成的2n位数,即n+1个0和n-1个1组成的2n位数必对应一个不符合要求的数。
因而不合要求的2n位数与n+1个0,n-1个1组成的排列一一对应。
显然,不符合要求的方案数为c(2n,n+1)。由此得出输出序列的总数目=c(2n,n)-c(2n,n+1)=c(2n,n)/(n+1)=h(n)。
类似问题 买票找零
有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?(将持5元者到达视作将5元入栈,持10元者到达视作使栈中某5元出栈)
将入栈出栈抽象成01序列即可带入模型
凸多边形三角划分
在一个凸多边形中,通过若干条互不相交的对角线,把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n,求不同划分的方案数f(n)。比如当n=6时,f(6)=14。
分析
如果纯粹从f(4)=2,f(5)=5,f(6)=14,……,f(n)=n慢慢去归纳,恐怕很难找到问题的递推式,我们必须从一般情况出发去找规律。
因为凸多边形的任意一条边必定属于某一个三角形,所以我们以某一条边为基准,以这条边的两个顶点为起点P1和终点Pn(P即Point),将该凸多边形的顶点依序标记为P1、P2、……、Pn,再在该凸多边形中找任意一个不属于这两个点的顶点Pk(2<=k<=n-1),来构成一个三角形,用这个三角形把一个凸多边形划分成两个凸多边形,其中一个凸多边形,是由P1,P2,……,Pk构成的凸k边形(顶点数即是边数),另一个凸多边形,是由Pk,Pk+1,……,Pn构成的凸n-k+1边形。
此时,我们若把Pk视为确定一点,那么根据乘法原理,f(n)的问题就等价于——凸k多边形的划分方案数乘以凸n-k+1多边形的划分方案数,即选择Pk这个顶点的f(n)=f(k)×f(n-k+1)。而k可以选2到n-1,所以再根据加法原理,将k取不同值的划分方案相加,得到的总方案数为:f(n)=f(2)f(n-2+1)+f(3)f(n-3+1)+……+f(n-1)f(2)。看到此处,再看看卡特兰数的递推式,答案不言而喻,即为f(n)=h(n-2) (n=2,3,4,……)。
最后,令f(2)=1,f(3)=1。
此处f(2)=1和f(3)=1的具体缘由须参考详尽的“卡特兰数”,也许可从凸四边形f(4)=f(2)f(3)+ f(3)f(2)=2×f(2)f(3)倒推,四边形的划分方案不用规律推导都可以知道是2,那么2×f(2)f(3)=2,则f(2)f(3)=1,又f(2)和f(3)若存在的话一定是整数,则f(2)=1,f(3)=1。(因为我没研究过卡特兰数的由来,此处仅作刘抟羽的臆测)。
类似问题
一位大城市的律师在她住所以北n个街区和以东n个街区处工作。每天她走2n个街区去上班。如果她从不穿越(但可以碰到)从家到办公室的对角线,那么有多少条可能的道路?
在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数?
给定节点组成二叉搜索树
(能构成h(N)个)
(这个公式的下标是从h(0)=1开始的)
n对括号正确匹配数目
给定n对括号,求括号正确配对的字符串数,例如:
0对括号:[空序列] 1种可能
1对括号:() 1种可能
2对括号:()() (()) 2种可能
3对括号:((())) ()(()) ()()() (())() (()()) 5种可能
那么问题来了,n对括号有多少种正确配对的可能呢?
考虑n对括号时的任意一种配对方案,最后一个右括号有唯一的与之匹配的左括号,于是有唯一的表示A(B),其中A和B也是合法的括号匹配序列
假设S(n)为n对括号的正确配对数目,那么有递推关系S(n)=S(0)S(n-1)+S(1)S(n-2) +...+S(n-1)S(0),显然S(n)是卡特兰数。
扩展
编辑对于在n位的2进制中,有m个0,其余为1的catalan数为:C(n,m)-C(n,m-1)。证明可以参考标准catalan数的证明。[7]
问题1的描述:有n个1和m个-1(n>m),共n+m个数排成一列,满足对所有0<=k<=n+m的前k个数的部分和Sk > 0的排列数。 问题等价为在一个格点阵列中,从(0,0)点走到(n,m)点且不经过对角线x==y的方法数(x > y)。
考虑情况I:第一步走到(0,1),这样从(0,1)走到(n,m)无论如何也要经过x==y的点,这样的方法数为(( n+m-1,m-1 ));
考虑情况II:第一步走到(1,0),又有两种可能:
a . 不经过x==y的点;(所要求的情况)
b . 经过x==y的点,我们构造情况II.b和情况I的一一映射,说明II.b和I的方法数是一样的。设第一次经过x==y的点是(x1,y1),将(0,0)到(x1,y1)的路径沿对角线翻折,于是唯一对应情况I的一种路径;对于情况I的一条路径,假设其与对角线的第一个焦点是(x2,y2),将(0,0)和(x2,y2)之间的路径沿对角线翻折,唯一对应情况II.b的一条路径。
问题的解就是总的路径数 ((n+m, m)) - 情况I的路径数 - 情况II.b的路径数。
((n+m , m)) - 2*((n+m-1, m-1))
或:((n+m-1 , m)) - ((n+m-1 , m-1))
问题2的描述:有n个1和m个-1(n>=m),共n+m个数排成一列,满足对所有0<=k<=n+m的前k个数的部分和Sk >= 0的排列数。(和问题1不同之处在于此处部分和可以为0,这也是更常见的情况) 问题等价为在一个格点阵列中,从(0,0)点走到(n,m)点且不穿过对角线x==y的方法数(可以走到x==y的点)。
把(n,m)点变换到(n+1,m)点,问题变成了问题1。
方法数为:
((n+m+1, m)) - 2*((n+m+1-1, m-1))
或:((n+m+1-1, m)) - ((n+m+1-1, m-1))
摘自百度百科

