参考:
https://blog.csdn.net/vivid117/article/details/101427302
http://wscentity.lofter.com/post/1d00edbd_6476453
Verilog中有符号与无符号的加法和乘法运算
无符号乘法和加法
对于无符号的乘法和加法,没有什么好说的,就是直接用‘*’和‘+’。
有符号乘法和加法
有符号和无符号运算
verilog里如果有符号数和无符号数做运算,会强制当作无符号运算
这就涉及verilog处理运算时的法则:
例如 c = a + b; 其中a和b都是四位数,c是五位。在计算时,verilog会将a和b都扩展到5位,然后再做加法,而如果a和b中有无符号数,则位宽扩展就按照无符号数来,也就是高位补0。所以如果a和b中既有无符号又有有符号,结果就不正确了。
解决方法是用 $signed()来修饰:c = a + $signed(b)这样在c = a + b,这个运算开始的扩位就会按照有符号数的方式进行扩位,在高位补符号位,加法得出的结果就是a、b视为有符号数的结果。
例子:
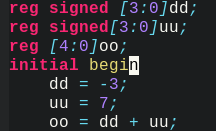 |||
||| 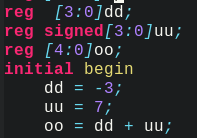 |||
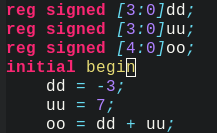
||| 
 |||
|||  |||
||| 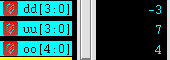
可见结果是不是signed倒是无所谓的。但是最好还是加上。
有符号数乘法
例如有符号数[3:0]a * [3:0]b. 其中a=-5,b=7。a用补码表示为1011,b用补码表示是0111,对于这个例子,乘法过程如下:
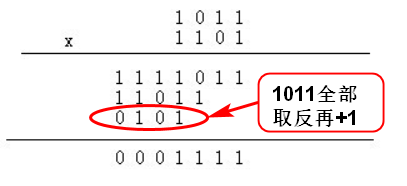
可以看到上面最后一行的结果需要对a进行(color{red}{取反加一})才正确,并且此时(color{red}{取反加一也包括a的符号位})。
另外,还需要注意的是所有部分积都要补符号位补到乘法输出值的位数。
其实乘法器就是由加法组成,所以b中的每一位跟a做乘法(异或)之后把部分积累加时,仍然需要遵从加法的原则,扩展符号位直到达到输出位宽,然后再加。
所以有符号乘法跟无符号乘法的区别就在这,无符号乘法不需要考虑符号位扩展问题,而有符号乘法在累加部分积的时候需要做符号位扩展,并且还要考虑符号位参与乘法时的含义不同,也就是说符号位的0表示0,但1却表示-1,所以符号位的1做乘法就不是异或而是(color{red}{对所有位取反再加一})了。
有符号乘法器的实现
上面说的是对于补码形式的有符号数如何计算乘法,而实际上上面这种方法是将符号位也参与到运算中,这种方式实际上需要区分符号位的乘法,所以在设计带符号乘法器时可能需要修改传统无符号乘法器中的加法器类型,可以参考:
https://blog.csdn.net/iteye_3619/article/details/82282317
在verilog中,一般有符号乘法器的做法是先将补码的输入都转成原码,再将符号位单独拿出来进行异或,然后其余部分当作无符号数乘起来,最后再对结果取补码转回原码结果。