链接:http://www.zhihu.com/question/20298134/answer/37952808
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
本回答想从一个更系统的角度来叙述pathfinding这一系列问题,希望可以成为一个更容易理解的tutorial。这里所涉及的寻路算法不限于RTS游戏,其中一些方法可能更适合静态的游戏环境。
这个回答中所包含的topics涉及
1.游戏地图的划分及其优劣性,这里包括:
- Grid (方格)
- Navigation Mesh(导航网格)
2.游戏中常用的搜寻算法及其优劣性
- A Star search
- Dijkstra’s algorithm
- Floyd-Warshall algorithm
首先假设我们有下面这样一个游戏地图
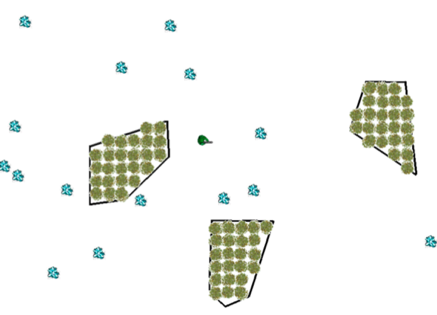
我们想使我们的小人从地图任意一个位置出发,都可以顺利避过障碍物到达另一个目的地。这时候该怎么做呢?
假设我们现在只有一张上面的地图,这时候小人是不能动的,因为我们需要告诉他哪些地方可以走。由此引入了第一个topic,也就是方格grid。
这个方法很简单,我只需要选择一个合适的正方形的边的大小,然后在地图上没有障碍物的地方画square就可以了。然后我们可以选取每一个square的中心,作为小人实际可以走的点,这样这个地图就成了下图模样(图中绿色的方格代表每一个grid,方格的中心才是可以走的点)。
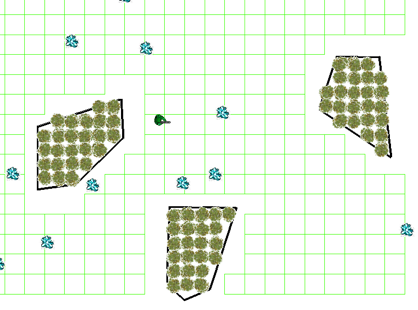
有了这些网格,我们只是告诉了小人哪些点是可以走的,但我们还要告诉它在某一个点上有哪些路径可以选择。这个很简单,我们可以选择某一个点周围八个点作为可以走的路径(如果这个方向没被障碍物挡住的话)。对所有的点重复这一过程,我们就可以生成这个地图的path networks(路径网络)了。如下图,图中蓝色的线代表路径网络。
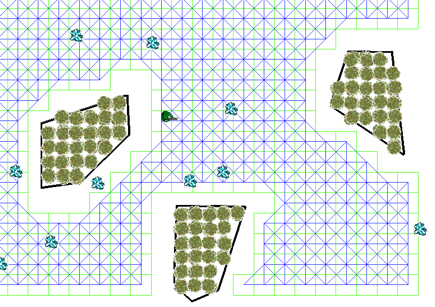
此时我们就已经完成了对连续的地图离散化这一过程,小人也就可以在游戏世界里乱走了(注意是乱走~)。这是因为我们还没有使用搜索算法来告诉小人如何到达目的的,或者说走哪条路可以到达目的地。
以上就是grid navigation的大致方法了,在此总结一下它的优缺点。
优点:这是一种对地图离散化的方法。这种方法真的很简单,非常容易实现而且容易和A star search或者uniform cost search算法结合起来使用。
缺点:使用这种方法划分出来的网格,小人的移动其实是不连续的。有时可能看起来并不自然,就如下图所示的情况。而且可以从上图看出,网格数灰常的多,可能需要大量的资源来计算和存储路径。
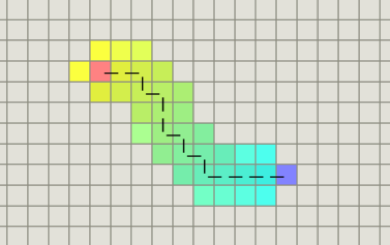
在说明常用的搜寻算法之前,我想详细说明一种游戏中更常用的路径生成方法,这就是navigation mesh(导航网格)。这里的mesh和grid有区别,mesh可以是很多种形状的多边形。下图中的每一个多边形都是navigation mesh的组成部分,魔兽世界就用到了这种方法进行地图的划分。
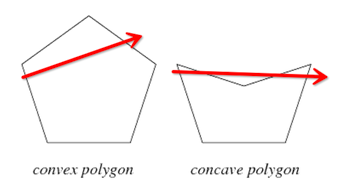
请注意这里的划分出的每一个多边形都是凸多边形。这里其实是使用到了凸多变形的性质,在凸多边形边上的一个点走到另外一点,不管怎么走都不会走出这个多边形,如下图所示(参考Convex Polygon -- from Wolfram MathWorld)。相反凹多边形就不满足这一性质。
应用到游戏世界里,我们只要在空地上放置凸多边形,小人在多边形内怎么走都不会碰到障碍。
这种方法听上去挺简单,实际该怎么操作呢。我们知道任意一个三角形都是凸多边形,我们可以先通过地图的边界点和障碍物的边界点,将地图划分成很多个三角形,如下图所示。
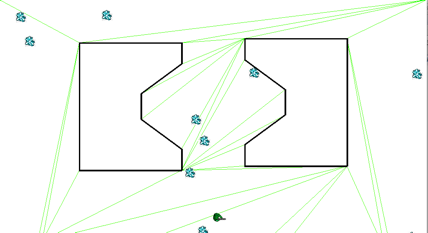
我们可以看到,虽然通过这种方法生成的网格相比grid已经大大减少,但是图上很多相邻的三角形是可以合并形成新的凸多边形的。所以我们其实还可以进一步优化,将可以合并成新的凸多边形的相邻多边形合并,并重复这一过程,最终得到下图。
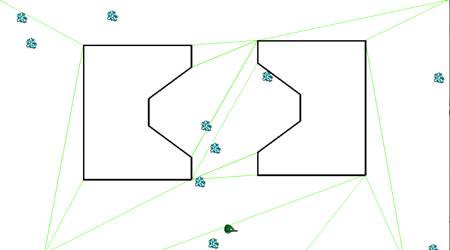
然后我们可以在每一个网格每一条边的中点上放置pathnode(路径点),然后将每一个网格自己边上的路径点连接起来就得到了完整的路径网络了,如下图,同上绿色的线代表画好的navigation mesh,蓝色的线代表可以走的路径网络。
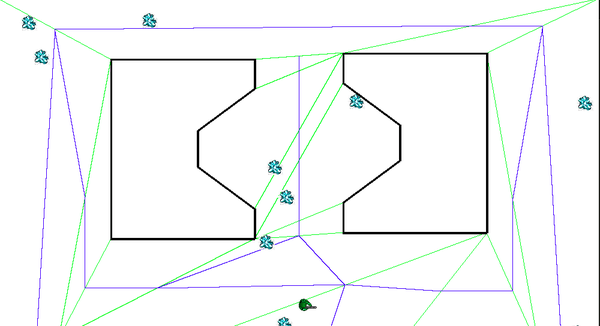
以上就是navigation mesh的大致思想与方法,其优缺点总结如下,参考(http://en.wikipedia.org/wiki/Navigation_mesh#Advantages):
优点:这种方法可以大大减少路径点和搜寻所需的计算量,同时也使小人的移动更加自然。在这样的路径点之间行走,我们其实可以完全无视地图上的任何障碍物。
缺点:计算三角形和合并相邻的凸多边形需要很大的计算量,而且实现起来没有看上去那么简单。不过成熟的游戏引擎一般是有现成的解决方案的。
在有了path network(路径网络)后,我们就可以开始考虑如果让小人从一点走到另外一点,如果寻找最优路线了(即返回一系列路径点)。
首先大多数人会想到A* search。A*是一种非常经典的搜索算法,使用到了heuristic和accumulated cost,细节这里就不赘述了,不太清楚的可以参考(A*_search_algorithm)。值得注意的是,这里的heuristic一般是admissible的,也就是说在A*中我们对目标的估计必须小于或等于其实际值,不然可能会出现找不到最优路径或者根本找不到路径的情况。当然也有很多情况下我们根本不需要找到最优路径,只要player觉得合理,who cares optimality呢lol~
这里除去A*的实现细节,我想说明的是,A*是一种single source single destination的算法,它的时间复杂度是O(|E|), E是地图上所有路径点所形成的路径网络的edge的数目。也就是说A*可以用来计算从一个点到另外一个点的最优路径。这也就说明A*适合用来对动态环境进行路径计算,可以实时根据当时的环境立即计算出路径。相对应的,Dijkstra’s algorithm和Floyd-Warshall适合对于不变的环境来进行计算,下面会说明为什么。
这里介绍的第二种寻路算法就是Dijkstra’s algorithm。说Dijkstra是A*的无heuristic版本,其实并不准确。A*去掉heuristic其实是uniform cost search。而Dijkstra是uniform cost search的multiple destination的变形。也就是说,给出地图上一个路径点,使用Dijkstra可以对地图上所有其他的路径点一次性计算出最优路径。Dijkstra的时间复杂度是O(|E|+|V|log|V|),这时E是edge数,V是vertex的数目(Dijkstra's_algorithm)。从这里可以看出,如果需要对地图上所有的路径点同时计算左右路径,Dijkstra会比使用A*更方便。这也就说明了为什么Dijkstra适合对静态的环境进行计算,因为静态的环境是不会变的,我们可以是用Dijkstra对地图进行preprocess获得navigation table(后面会说明navigation table如何生成)。我们可以把navigation table记录下来,这样在游戏进行的时候从一个路径点到另外一个路径点只需要查表就可以了,这样一来游戏实际运行时的寻路的时间复杂度就减少到了O(V),也就是线性复杂度了,而且对于静态的环境,我们的navigation table是百分之百可靠的。
另外还想简要介绍一种寻路算法Floyd-Warshall。这个算法是all sources all destinations的,也就是说给出一个地图,这个算法可以计算出从所有路径点到所有其他路径点的最优路径,而且可以一边运行算法一边生成navigation table,而Dijkstra需要先跑一遍算法,然后从一个路径点backtrack才能生成navigation table。这个算法的时间复杂度是O(|V|^3),详情可以参考Floyd。
至于Navigation table, 它大概是长这样的,假设地图上已经通过上述的grid或navigation mesh生成了5个路径点,表示为0到4。表上的数字代表了从某一点要到另外一个点,应该走哪个相临的点,再从走到的下一个点继续查表。
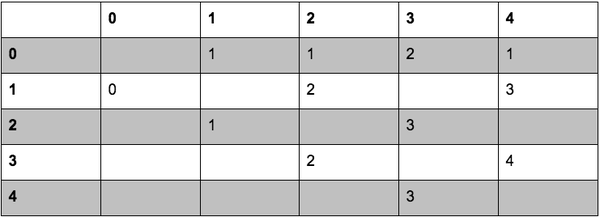
假设我们已经通过运行Dijkstra和Floyd-Warshall生成了这个navigation table。如果我们需要找到从第0个点到第4的点的最优路径,我们可以查表上第0行的第4列,列上的数字是1,意思是要从0走到4,第一个要走的点是1;再查第一行第四列,下一个要走的点是3;再查第三行第四列,我们就可以通过3走到目的地4了。这一系列0-1-3-4就是之前计算出的最优路径。这种方法对于静态的环境十分有效,只要环境不变,通过提前计算navigation table,在游戏实际运行时只需要O(|V|)的时间复杂度就可以获得到达目标点的最优路径了。
总结:
A* search:single source single destination,速度较快但依赖于heuristic函数的设计。适用于动态环境的寻路,因此适合RTS。
Dijkstra's Algorithm:single souce all destinations,速度也比较快,不需要heuristic函数,但是在建立navigation table的时候需要backtrack。适用于静态环境的寻路。
Floyd-Warshall Algorithm: all sources all destinations,可以在算法运行过程中建立navigation table。适用于静态环境的寻路。
对于即时战略游戏,地图中所涉及的环境多是动态,所以A*可能更适合一些。