最近学习数论来着,然后就萌生了一个整理一个数论题板子集合的想法
不过,会推数学式子才是数论题的关键,数学才是数论题的基础与核心
Code:
int gcd(int a,int b) { if(a % b == 0) return a; return gcd(b,a % b); }
Exgcd:
目的是求: ax + by = gcd(a,b)的一组解(x,y)
同时返回的是d = gcd(a,b)
Code:
int Exgcd(int a,int b,int &x,int &y) { if(!b) { x = 1; y = 0; return a; } else { int d = Exgcd(b,a%b,x,y); int t = x; x = y; y = t - (a / b) * y; } }
这个算法是主要用来判断某一个数是不是质数的算法
但是请注意这个算法具有随机性,而且是单点判断,不适用于区间的素数筛选
这个算法的证明(手写):

Code:
int gg[8] = {2,3,5,7,13,29,37,89}; Miller_Rabin(int a,int n) { int d = n - 1; int r = 0; while(d % 2 == 0) { d /= 2; r++; } int x = kuaisumi(a,d,n); if(x == 1) return true; for(int i=0;i<r;i++) { if(x == n - 1) return true; x = (long long)x * x % n; } return false; } bool is_prime(int n) { if(n <= 1) return false; for(int a=0;a<8;a++) if(n == gg[a]) return true; for(int a=0;a<8;a++) if(!Miller_Rabin(gg[a],n)) return false; return true; }
线性筛:
线性筛的算法有很多种,但是本文这里为了简便起见
只介绍欧拉筛了,同时因为欧拉筛可以预处理莫比乌斯函数和欧拉函数等数论函数
还可以得出每一个合数的最小非1因子
好处多多a
Code:
memset(not_prime,0,sizeof(not_prime)); for(int i=2;i<=n;i++) { if(!not_prime[i]) { prime[++prime_cnt] = i; phi[i] = i - 1; mu[i] = -1; } for(int j=1;j<=prime_cnt;j++) { int x = i * prime[j]; if(x > n) break; not_prime[x] = true; phi[x] = phi[i] * phi[prime[j]]; mu[x] = mu[i] * mu[prime[j]]; if(i % prime[j] == 0) { phi[x] = phi[i] * prime[j]; mu[x] = 0; break; } } }
快速幂:
这个的原理就是在实现的时候将每一个数将其"拆分"
从而我们可以用倍数来×代替了×多少次
Code:
int quickpow(int a,int b,int p) { int res = 1; while(b) { if(b & 1) res = res * a % p; a = a * a % p; b >>= 1; } return res; }
中国剩余定理:
定理内容:
中国剩余定理的形式是这样的:
存在一个这样的式子:(中国剩余定理的限制条件:m1,m2,m3...mn这些数是互质的)
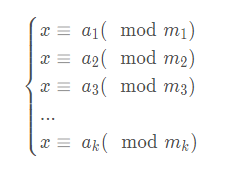
然后我们的任务是求最小的整数x使得非负整数x满足以上条件
我们设定一个 M = ∏mi (即M为所有m的最小公倍数)
方程 M / mi * ti ≡ 1 (mod mi) 中 ti 为其最小非负整数解 (这里可以用exgcd来实现求解)
那么有一个解为 x = ∑ ai * M / mi * ti
通解为: x + i * M
特别地,算法的非负整数解为 (x % M + M) % M (将x移到[0,M]这个区间内)
算法证明:
因为M / mi 是除了mi之外的所有数的倍数
那么对于任意的k ≠ i 都有 ai * M / mi * ti ≡ 0 (mod mk)
又有M / mi * ti ≡ 1 (mod mi)
将两边同时乘ai得 ai * M / mi * ti ≡ ai (mod mi)
最后我们带入x = ∑ ai * M / mi * ti
从而原方程组成立
Code:
void exgcd(int a,int b,int &x,int &y) { if(b == 0) { x = 1; y = 0; return ; } exgcd(b,a % b,x,y); int t = x; x = y; y = t - a / b * y; } int crt() { int ans = 0; int M = 1; int x,y; for(int i=1;i<=k;i++) M *= b[i]; for(int i=1;i<=k;i++) { int t = M / b[i]; exgcd(t,b[i],x,y); x = (x % b[i] + b[i]) % b[i]; ans = (ans + t * x * a[i]) % M; } return (ans + M) % M; }
拓展中国剩余定理
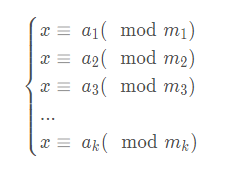
这个与中国剩余定理不同的地方就在于这里的mi不一定两两互质了
解法:
我们假设已经求解出前k - 1个同余方程组的解为x
并且有M=∏(i−1,k−1)mi
那么前k个方程组的通解为 x + i * M(i ∈ Z)
对于我们即将插入第k个方程后形成的k个方程形成的方程组
我们就是要求一个正整数t,使得
x + t * M ≡ ak (mod mk)
我们针对于这一个式子转化一下就可以得到:
t * M ≡ ak - x (mod mk)
我们可以利用exgcd求解t
若这一个方程组无解t那么这整个方程组也就是无解的(显然,我们无法找到一个x使得x满足以上的方程成立条件)
若有,则前k个同余式构成的方程组的一个解为:
xk = x + t * M
所以我们整个算法的核心思路就是我们求解k次exgcd对于方程进行了k - 1次的展开
Code:
int exgcd(int a,int b,int &x,int &y) { if(b == 0) { x = 1; y = 0; return a; } int d = exgcd(b,a % b,x,y); int t = x; x = y; y = t - a / b * y; return d; } int excrt() { int x,y,k; int M = b[1]; int ans = a[1]; for(int i=2;i<=n;i++) { int aa = M; int bb = b[i]; int c = (a[i] - ans % bb + bb) % bb; // x + t * M ≡ ak (mod mk) int d = exgcd(aa,bb,x,y); //求一组解 int m = bb / d; if(c % d != 0) //若无解就直接返回 return -1; x = x * (c / d) % m; ans += x * M; M *= m; //要将这个mi加入到M里面 ans = (ans % M + M) % M; // xk = x + t * M } return (ans % M + M) % M; //返回值 }
放两道模板题:
BSGS(Baby Step Giant Step)算法
它还可以找循环节!
其实它还叫(拔山盖世算法qwq)
这个算法的问题主要就是求解已知A, B, C,求X使得A^x = B (mod C)
然后这个算法的核心思路就是分块枚举(也就是比较好看的暴力)
我们需要完整地算出第一行的所有数的值
在第二行及以后我们便可以对于每一行都进行二分运算(这里我们对于它进行排序便于二分)
我们判断在每一行的值有没有等于的地方
最后就可以在有这个函数值的一行进行算找那一个特殊值就好了(对于取模运算可以在快速幂的时候注意一下)
分块的大小是sqrt() * sqrt()的
而接下来将给出为什么是sqrt()的证明
因为 x = i*m-j , 所以x 的最大值不会超过p
由费马小定理知: 当p为质数且 (a,p) = 1 时 ap-1 ≡ 1 (mod p)
所以 当 x = p-1 时 ap-1 ≡ 1 会重新开始循环 所以 x 最大不会超过 p-1
所以:如果枚举 x 的话枚举到 p 即可。
所以使 im−j<=p , 即 m=⌈√p⌉ , i,j 最大值也为m。
Code:
int size; bool erfen(int x) { int l = 0; int r = size; while(l + 1 != r) { int m = (l + r) >> 1; if(z[m] >= x) r = m; else l = m; } return z[r] == x; } int BSGS(int a,int b,int p) { size = sqrt(p); int nowv = 1; for(int i=1;i<=size;i++) { nowv = (long long) nowv * a % p; z[i] = nowv; if(z[i] == b) return i; } sort(z + 1,z + size + 1); for(int i=2;(i - 1) * size + 1<=p;i++) { int y = (long long)b * kuaisumi(kuaisumi(a,size * (i - 1),p),p - 2,p); if(erfen(y)) { for(int j=(i - 1) * size + 1;j<=i*size;j++) if(kuaisumi(a,j,p) == b) return j; } } return -1; }
未完待续···