链接:https://www.zhihu.com/question/20924039/answer/131421690
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
r(d)可以理解为有d的参数进行约束,或者 D 向量有d个维度。
咱们将楼主的给的凸优化结构细化一点,别搞得那么抽象,不好解释;
, 其中,
咱们可以令: f() =
.
ok,这个先介绍到这里,至于f(x)为什么用多项式的方式去模拟?相信也是很多人的疑问,很简单,大家看看高等数学当中的泰勒展开式就行了,任何函数都可以用多项式的方式去趋近,log x,lnx,
等等都可以去趋近,而不同的函数曲线其实就是这些基础函数的组合,理所当然也可以用多项式去趋近,好了,这个就先解释到这里了。
接下来咱们看一下拟合的基础概念。
首先,用一个例子来理解什么是过拟合,假设我们要根据特征分类{男人X,女人O}。
请看下面三幅图,x1、x2、x3;
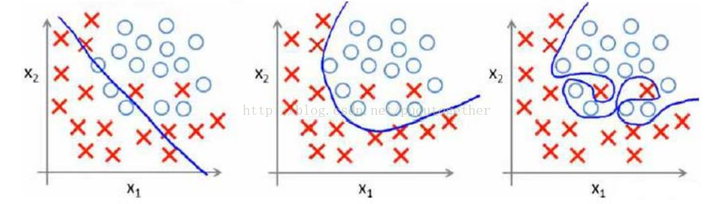
这三幅图很容易理解:
1、 图x1明显分类的有点欠缺,有很多的“男人”被分类成了“女人”。
2、 图x2虽然有两个点分类错误,但是能够理解,毕竟现实世界有噪音干扰,比如有些人男人留长发、化妆、人妖等等。
3、 图x3分类全部是正确的,但是看着这副图片,明显觉得过了,连人妖都区分的出来,可想而知,学习的时候需要更多的参数项,甚至将生殖器官的形状、喉结的大小、有没有胡须特征等都作为特征取用了,总而言之f(x)多项式的N特别的大,因为需要提供的特征多,或者提供的测试用例中我们使用到的特征非常多(一般而言,机器学习的过程中,很多特征是可以被丢弃掉的)。
好了,总结一下三幅图:
x1我们称之为【欠拟合】
x2我们称之为【分类正拟合】,随便取的名字,反正就是容错情况下刚好的意思。
x3我们称之为【过拟合】,这种情况是我们不希望出现的状况,为什么呢?很简单,它的分类只是适合于自己这个测试用例,对需要分类的真实样本而言,实用性可想而知的低。
恩,知道了过拟合是怎么回事之后,我们来看一下如何去规避这种风险。先不管什么书上说的、老师讲的、经验之说之类的文言文。咱们就站在第一次去接触这种分类模型的角度去看待这个问题,发散一下思维,我们应该如何去防止过拟合?
显而易见,我们应该从【过拟合】出现的特征去判别,才能规避吧?
显而易见,我们应该、而且只能去看【过拟合】的f(x)形式吧?
显而易见,我们从【过拟合】的图形可以看出f(x)的涉及到的特征项一定很多吧,即等等很多吧?
显而易见,N很大的时候,是等数量增长的吧?
显而易见,w系数都是学习来的吧?
So,现在知道这些信息之后,如何去防止过拟合,我们首先想到的就是控制N的数量吧,即让N最小化吧,而让N最小化,其实就是让W向量中项的个数最小化吧?
其中,W=()
PS: 可能有人会问,为什么是考虑W,而不是考虑X?很简单,你不知道下一个样本想x输入的是什么,所以你怎么知道如何去考虑x呢?相对而言,在下一次输入,即第k个样本之前,我们已经根据
次测试样本的输入,计算(学习)出了W.就是这么个道理,很简单。
ok,any way.回到上面的思维导图的位置,我们再来思考,如何求解“让W向量中项的个数最小化”这个问题,学过数学的人是不是看到这个问题有点感觉?对,没错,这就是0范数的概念!什么是范数,我在这里只是给出个0-2范数定义,不做深究,以后有时间在给大家写点文章去分析范数的有趣玩法;
0范数,向量中非零元素的个数。
1范数,为绝对值之和。
2范数,就是通常意义上的模。
PS,貌似有人又会问,上面不是说求解“让W向量中项的个数最小化”吗?怎么与0范数的定义有点不一样,一句话,向量中0元素,对应的x样本中的项我们是不需要考虑的,可以砍掉。因为没有啥意义,说明
项没有任何权重。so,一个意思啦。
ok,现在来回答楼主的问题,r(d) = “让W向量中项的个数最小化” =
所以为了防止过拟合,咱们除了需要前面的相加项最小,即楼主公式当中的 =
最小,我们还需要让r(d)=
最小,所以,为了同时满足两项都最小化,咱们可以求解让
和r(d)之和最小,这样不就同时满足两者了吗?如果r(d) 过大,
再小也没用;相反r(d)再小,
太大也失去了问题的意义。
说到这里我觉得楼主的问题我已经回答了,那就是为什么需要有个r(d)项,为什么r(d)能够防止过拟合原因了。
根据《男人帮》电影大结局的剧情:本来故事已经完成了,为了让大家不至于厌恶课本的正规理论,我们在加上一集内容,用以表达我对机器学习出书者的尊重;
书本中,或者很多机器学习的资料中,为了让全球的机器学习人员有个通用的术语,同时让大家便于死记硬本,给我上一段黑体字的部分的内容加上了一坨定义,例如:
我们管叫做经验风险,管上面我们思维导图的过程叫做正则化,所以顺其自然的管r(d)叫做正则化项,然后管
+r(d) 叫做结构风险,所以顺其自然的正则化就是我们将结构风险最小化的过程,它们是等价的。
By the way,各位计算机界的叔叔、阿姨、伯伯、婶婶,经过不懈的努力,发现了这个公式很多有意思的地方,它们发现0范数比较恶心,很难求,求解的难度是个NP完全问题。然后很多脑袋瓜子聪明的叔叔、阿姨、伯伯、婶婶就想啊,0范数难求,咱们就求1范数呗,然后就研究出了下面的等式:

一定的条件我就不解释了,这里有一堆算法,例如主成分KPCA等等,例子我就不在举了,还是原话,以后我会尽量多写点这些算法生动点的推到过程,很简单,注重过程,不要死记硬背书本上的结果就好。
上面概括而言就是一句话总结:1范数和0范数可以实现稀疏,1因具有比L0更好的优化求解特性而被广泛应用。然后L2范数,是下面这么理解的,我就直接查别人给的解释好了,反正简单,就不自己动脑子解释了:
L2范数是指向量各元素的平方和然后求平方根。我们让L2范数的正则项||W||2最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0,这里是有很大的区别的哦;所以大家比起1范数,更钟爱2范数。
所以我们就看到书籍中,一来就是,r(d)=
min{
都是这么来的啦,万变不离其中。
讲一点自己机器学习过程的体验,大家都觉得机器学习入门难,绝大部分人反应知其然不知其所以然,这个原因很多时候在于中国教育工作者的教学、科研氛围,尤其是中文书籍出书者自己都不去搞懂原理,一个劲的为了利益而出书、翻译书,纯粹利益驱动。再加之机器学习起源于国外,很多经典的、有趣的历史没有被人翻译、或者归类整理,直接被舍弃掉了。个人感觉这是中国教育的缺失导致的。希望更多的人真的爱好计算机,爱好机器学习以及算法这些知识。喜欢就是喜欢。希望国内机器学习的爱好者慢慢的齐心合力去多多引荐这些高级计算机知识的基础。教育也不是由于利益而跟风,AI热出版社就翻译AI,机器学习热就翻译机器学习,知识层面不断架空,必然导致大家学习热情的不断衰减!愿共勉之。