逆卷积:convtranspose2d(fractionally-strided convolutions)
1.首先先定义进行卷积的参数:
- 输入特征图为高宽一样的Hin*Hin大小的x
- 卷积核大小kernel_size
- 步长stride
- padding填充数(填充0)
- 输出特征图为Hout*Hout大小的y
计算式子为:
Hout = floor( Hin + 2*padding - kernel_size / stride) + 1
2.然后实现上面的卷积的转置卷积
定义其参数为:
- 输入特征图为高宽一样的Hout*Hout大小的y
- 卷积核大小kernel_size
- 步长stride
- paddingnew 填充数(填充0)
- 输出特征图为Hin*Hin大小的x
逆卷积的过程主要分两步:
- 对输入的特征图y进行变换,得到新的特征图ynew
- 内部变换,与卷积时设置的stride相关
- 外部变换,与卷积时设置的padding相关
- 根据得到的特征图进行卷积即可
1)对输入的特征图y进行变换,得到新的特征图ynew
1》内部变换
当卷积时设置的stride>1时,将对输入的特征图y进行插值操作(interpolation)。
即需要在输入的特征图y的每个相邻值之间插入(stride-1)行和列0,因为特征图中能够插入的相邻位置有(height-1)个位置,所以此时得到的特征图的大小由Hout*Hout(Hout即height) 变为新的 Hout_new*Hout_new,即[Hout + (stride-1) * (Hout-1)] * [Hout + (stride-1) * (Hout-1)]
2》外部变换
为了实现由Hout*Hout大小的y逆卷积得到Hin*Hin大小的x,还需要设置paddingnew的值为(kernel_size - padding - 1),这里的padding是卷积操作时设置的padding值
所以计算式子变为:
Hin = floor( [Hout_new + 2*paddingnew - kernel_size] / stride') + 1
⚠️该式子变换后,定义向下取整的分母stride'值为定值1
Hout_new和paddingnew的值代入上面的式子,即变为:
Hin = floor( Hout + (stride-1) * (Hout-1) + 2*(kernel_size - padding - 1) - kernel_size) + 1
化简为:
Hin = floor( (Hout - 1) * stride - 2*padding + kernel_size - 1) + 1
= (Hout - 1) * stride - 2*padding + kernel_size
这样式子使的卷积Conv2d和逆卷积ConvTranspose2d在初始化时具有相同的参数,而在输入和输出形状方面互为倒数。
所以这个式子其实就是官网给出的式子:

可见这里没考虑output_padding
output_padding的作用:可见nn.ConvTranspose2d的参数output_padding的作用
3.下面举例说明
https://github.com/vdumoulin/conv_arithmetic#convolution-arithmetic
1)当stride=1时,就不会进行插值操作,只会进行padding,举例说明:
卷积操作为:
蓝色为输入特征图Hin*Hin=4*4,绿色为输出特征图Hout*Hout=2*2,卷积核kernel_size=3, stride=1
根据式子Hout = floor( Hin + 2*padding - kernel_size / stride) + 1
可得padding=0

其对应的逆卷积操作为:
蓝色为输入特征图Hout*Hout=2*2,绿色为输出特征图Hin*Hin=4*4,卷积核kernel_size=3, stride=1
卷积时的padding=0
将这些值代入上面的式子Hin = (Hout - 1) * stride - 2*padding + kernel_size
果然输入Hout*Hout=2*2能得到输出Hin*Hin=4*4
变形过程为:
paddingnew = kernel_size - padding -1 = 3 -0 -1 = 2
所以可见下方的蓝色最后的大小为7*7 = Hout + 2*paddingnew = 2 + 2*2 = 6

⚠️这里可见是有padding的,为什么定义是为no padding呢?
这是因为它对应的卷积操作的padding=0
1)当stride=2时,进行插值和padding操作,举例说明:
卷积操作为:
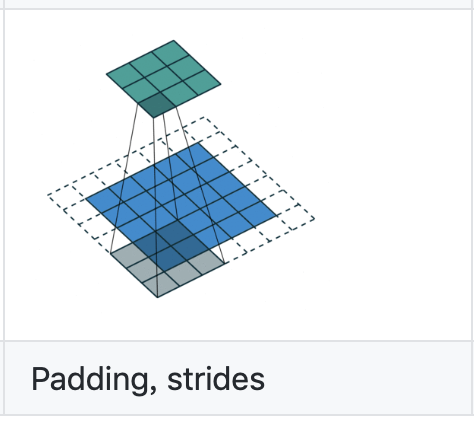
蓝色为输入特征图Hin*Hin=5*5,绿色为输出特征图Hout*Hout=3*3,卷积核kernel_size=3, stride=2
根据式子Hout = floor( Hin + 2*padding - kernel_size / stride) + 1
可得padding=1
其对应的逆卷积操作为:
蓝色为输入特征图Hout*Hout=3*3,绿色为输出特征图Hin*Hin=5*5,卷积核kernel_size=3,stride=2
卷积时的padding=1
将这些值代入上面的式子Hin = (Hout - 1) * stride - 2*padding + kernel_size
果然输入Hout*Hout=3*3能得到输出Hin*Hin=5*5
变形操作为:
Hout_new = Hout + (stride-1) * (Hout-1) = 3 + (2-1)*(3-1) = 5
paddingnew = kernel_size - padding -1 = 3 -1 -1 = 1
所以可见下方的蓝色最后的大小为7*7 = Hout_new + 2*paddingnew = 5 + 2*1 = 7
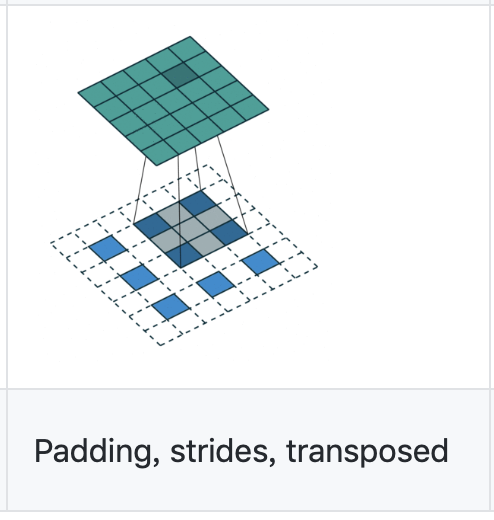
⚠️因为这里的逆卷积对应的卷积操作的padding= 1,所以这里不是no padding,而是padding