题目描述
一座城市建立在规则的n×m网格上,并且网格均由1×1正方形构成。在每个网格上都可以有一个建筑,建筑由若干个1×1×1的立方体搭建而成(也就是所有建筑的底部都在同一平面上的)。几个典型的城市模型如下图所示:
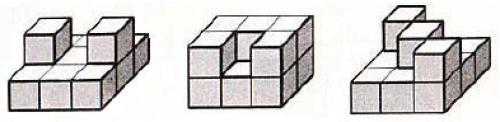
现在给出每个网格上建筑的高度,即每个网格上建筑由多少个立方体搭建而成,要求这个建筑模型的表面积是多少。
输入输出格式
输入格式:输入文件的第1行包含2个正整数n和m,为城市模型的长与宽。
接下来n行,每行m个数字字符,描述了网格每个格子高度(可见所有建筑高度都大等于0且小等于9)。
输出格式:输出文件包含一个非负整数,为城市模型的表面积。
输入输出样例
输入样例#1:
3 3 111 212 111
输出样例#1:
38
输入样例#2:
3 4 1000 0010 0000
输出样例#2:
12
说明
本题有2个测试数据
20%的数据满足:n, m≤10;
40%的数据满足:n, m≤100;
100%的数据满足:n, m≤1000。
#include<iostream> #include<cstdio> using namespace std; int h[1002][1002]={0},s=0; int fx[4]={-1,0,1,0},fy[4]={0,1,0,-1},p; char c; int main() { int n,m; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { char c; cin>>c; h[i][j]=c-'0'; } for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) { if(h[i][j])s+=2;//如果这一格的高度不为0,则上下两个面也要算进去 for(int k=0;k<4;k++) { p=h[i+fx[k]][j+fy[k]];// if(p<h[i][j])s+=h[i][j]-p;//找前后左右的格子,如果高度比这个格子矮。则说明该格子有突出的一部分,就要算上。 } } printf("%d",s); return 0; }