题目:
Problem Description
Bean-eating is an interesting game, everyone owns an M*N matrix, which is filled with different qualities beans. Meantime, there is only one bean in any 1*1 grid. Now you want to eat the beans and collect the qualities, but everyone must obey by the following rules: if you eat the bean at the coordinate(x, y), you can’t eat the beans anyway at the coordinates listed (if exiting): (x, y-1), (x, y+1), and the both rows whose abscissas are x-1 and x+1.
Now, how much qualities can you eat and then get ?

Now, how much qualities can you eat and then get ?
Input
There are a few cases. In each case, there are two integer M (row number) and N (column number). The next M lines each contain N integers, representing the qualities of the beans. We can make sure that the quality of bean isn't beyond 1000, and 1<=M*N<=200000.
Output
For each case, you just output the MAX qualities you can eat and then get.
Sample Input
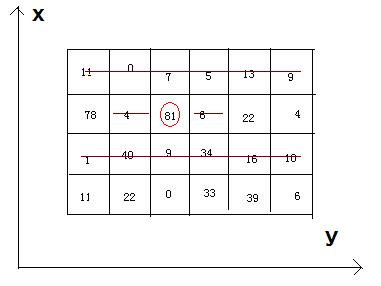
4 6
11 0 7 5 13 9
78 4 81 6 22 4
1 40 9 34 16 10
11 22 0 33 39 6
Sample Output
242
参 考 :http://972169909-qq-com.iteye.com/blog/1447073
题 意:
在图中取数,例如取了81之后,同一行的相邻两个不能取,还有81的上面那行和下面那行也不能取,问能取到的最大和是多少?
做法 :
最大连续子串和
代码:

1 //最大连续子串和 2 3 #include<iostream> 4 #include<stdio.h> 5 using namespace std; 6 7 const int T=200005; 8 9 int main( ){ 10 11 int n,m,A[T],B[T]; 12 while(~scanf("%d %d",&n,&m)){ 13 for( int i=1;i<=n;i++){ 14 for( int j=1;j<=m;j++){ 15 scanf("%d",&A[j]); 16 if( j==2 ) A[j]=max( A[j], A[j-1] ); 17 else if( j>2 ) A[j]=max( A[j]+A[j-2], A[j-1] ); 18 } 19 if( i==1 ) B[i]=A[m]; 20 else if(i==2) B[i]=max( A[m],B[i-1]); 21 else B[i]=max ( A[m]+B[i-2], B[i-1]); 22 } 23 cout << B[n] <<endl; 24 } 25 return 0; 26 }
