题目解析
想法还是比较难想到的。
把每棵生成树的(sum a_e)和(sum b_e)看成点对((x,y)),于是答案是(k=x imes y)最小的点对。由于边权都是非负数,所以可以看成是离坐标轴最近的反比例函数的系数。
怎么求这个点呢?
首先,分别找到离(x)轴,(y)轴最近的点
这个可以分别以(a_e,b_e)作为边权,求(MST)
不妨设离(x)轴最近的点是(A),离(y)轴最近的点是(B)
然后,找到一个在(AB)左下方,并且离(AB)最远的点(C)
可以等价为(S_ΔABC)最大,因为底为(AB)是定值,三角形面积越大,高越大,而高就是距离。
根据叉乘的几何意义,(S_ΔABC=frac{|vec{AB} imesvec{AC}|}{2})
注意到(vec{AB} imesvec{AC})是负数:(我还想了很久为啥它是负数,我一直以为叉乘顺序不一样(旋转方向不一样)只会影响最后生成的向量的方向(右手螺旋定理),但注意这里是有向面积)
如果是(vec{AB} imesvec{AC}),那么就是(vec{AB})逆时针转到(vec{AC}),转了优角,所以(sinθ<0),所以(vec{AB} imesvec{AC}=|vec{AB}| imes|vec{AC}| imes sinθ<0)
反之,如果是(vec{AC} imesvec{AB}),就是(vec{AC})逆时针转到(vec{AB}),转了劣角,所以乘出来(>0)
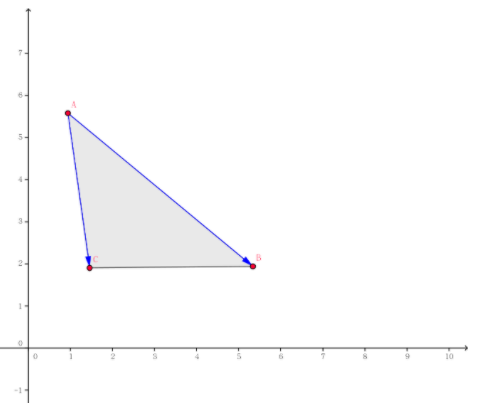
(图片来自于网络)
所以(S_ΔABC=-frac{vec{AB} imesvec{AC}}{2}),要最大化(S_ΔABC),只需要最小化(vec{AB} imesvec{AC})
根据叉乘的坐标表达形式:(vec{AB} imesvec{AC}\=(x_B-x_A)(y_C-y_A)-(x_C-x_A)(y_B-y_A)\ =(x_B-x_A)y_C+(y_A-y_B)x_C-(x_B-x_A)y_A+(y_B-y_A)x_A)
后面是常数,所以要最小化((x_B-x_A)y_C+(y_A-y_B)x_C),(x_C,y_C)是生成树的(sum),所以把边权赋成((x_B-x_A)b_e)和((y_A-y_B)a_e),然后求(MST)就可以得到(C)的坐标,用(C)的坐标更新答案。
递归AC,BC
把(AC,BC)拿去重复上述操作,递归处理,不断得到一个新的(C),更新答案。
直到算出来的(C)满足(vec{AB} imesvec{AC}),说明转过火了,这个时候的(C)在(AB)上方,结束递归。
点的编号居然是从(0)开始的,差评(雾
►Code View
#include<cstdio>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstring>
using namespace std;
#define N 205
#define M 10005
#define INF 0x3f3f3f3f
#define LL long long
int rd()
{
int x=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-')f=-1; c=getchar();}
while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
return f*x;
}
int n,m,f[N];
struct node{
int u,v,a,b,w;
}e[M];
struct Point{
int x,y;
};
Point ans;
int Cross(Point p,Point q)
{
return p.x*q.y-p.y*q.x;
}
bool cmp(node p,node q)
{
return p.w<q.w;
}
void Init()
{
for(int i=1;i<=n;i++)
f[i]=i;
}
int Find(int x)
{
if(f[x]==x) return x;
return f[x]=Find(f[x]);
}
bool Union(int u,int v)
{
u=Find(u),v=Find(v);
if(u==v) return 0;
if(u<v) f[u]=v;
else f[v]=u;
return 1;
}
Point Kruskal()
{
Point res; res.x=0,res.y=0;
Init();
sort(e+1,e+m+1,cmp);
int cnt=0;
for(int i=1;i<=m;i++)
{
if(!Union(e[i].u,e[i].v)) continue;
res.x+=e[i].a,res.y+=e[i].b;
cnt++;
if(cnt==n-1) break;
}
LL ret=1ll*ans.x*ans.y,now=1ll*res.x*res.y;
if(now<ret||(now==ret&&res.x<ans.x)) ans=res;
return res;
}
void solve(Point A,Point B)
{
for(int i=1;i<=m;i++)
e[i].w=(B.x-A.x)*e[i].b+(A.y-B.y)*e[i].a;
Point C=Kruskal();
Point D,E;
D.x=B.x-A.x,D.y=B.y-A.y;
E.x=C.x-A.x,E.y=C.y-A.y;
if(Cross(D,E)>=0) return ;
solve(A,C);
solve(C,B);
}
int main()
{
n=rd(),m=rd();
for(int i=1;i<=m;i++)
e[i].u=rd()+1,e[i].v=rd()+1,e[i].a=rd(),e[i].b=rd();
for(int i=1;i<=m;i++)
e[i].w=e[i].a;
ans.x=INF,ans.y=INF;
Point A=Kruskal();
for(int i=1;i<=m;i++)
e[i].w=e[i].b;
Point B=Kruskal();
solve(A,B);
printf("%d %d
",ans.x,ans.y);
return 0;
}