《大话数据结构》笔记（6-2）--树：二叉树

代码实现：

 

 

第六章    树：二叉树

定义

 特点

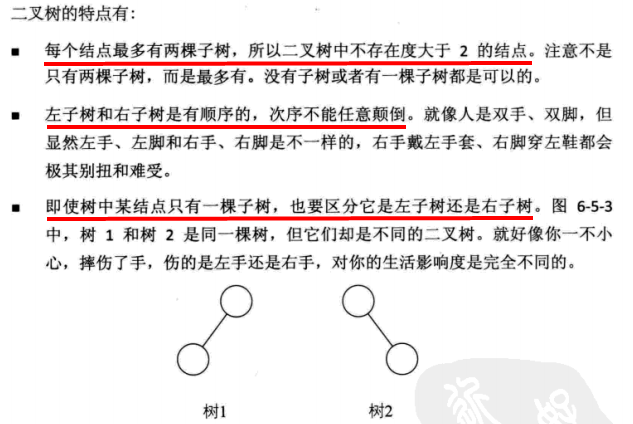
二叉树的五种基本形态：

1. 空二叉树

2. 只有一个根结点

3. 根结点只有左子树

4. 根结点只有右子树

5. 根结点基友左子树又有右子树

 

 

特殊二叉树

斜树

所有结点都只有左子树的二叉树叫做左斜树。所有结点都只有右子树的二叉树叫做右斜树。

这两者统称为斜树。

 

斜树有很明显的特点，就是每一层都只有一个结点，结点的个数与二叉树的深度相同。

其实线性表结构可以理解为树的一种极其特殊的表现形式。

 

满二叉树

在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层上，这样的二叉树称为满二叉树。

 

特点

1. 叶子只能出现在最下一层。

2. 非叶子结点的度一定是2.

3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

 

完全二叉树

对一棵具有n个结点的二叉树按层序编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树。如下图：

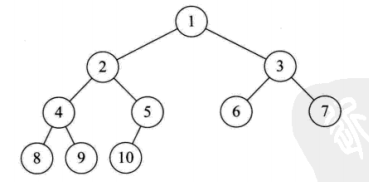
满二叉树一定是一棵完全二叉树，但完全二叉树不一定是满的。

 

特点

 

二叉树的性质

二叉树性质1

在二叉树的第 i 层上最多有2^i-1个结点（i>=1）.

 

二叉树性质2

深度为k的二叉树至多有2^k-1个结点（k>=1）.

 

二叉树性质3

对任何一棵二叉树T，如果其终端结点数为n₀，度为2的结点数为n₂，则n₀=n₂+1.

 

二叉树性质4

具有n个结点的完全二叉树的深度为最大整数）。

 

二叉树性质5

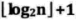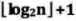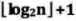如果对一棵有n个结点的完全二叉树（其深度为）的结点按层序编号（从第1层到第层，每层从左到右），对任一结点 i (1<=i<=n)有：

1. 如果i=1，则结点 i 是二叉树的根，无双亲；如果i>1，则其双亲是结点[i/2]。

2. 如果2i>n，则结点i无左孩子（结点 i 为叶子结点）；否则其左孩子是结点2i.

3. 如果2i+1>n，则结点 i 无右孩子；否则其右孩子是结点2i+1.

 

 

二叉树的存储结构

二叉树的顺序存储结构

就是用一维数组存储二叉树中的结点，并且结点的存储位置即数组的下标要能体现结点之间的逻辑关系。

 

完全二叉树的顺序存储：

 

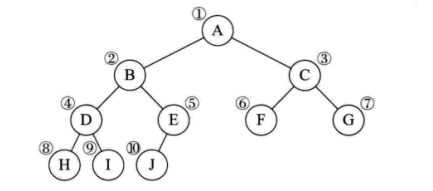
一般二叉树的顺序存储：

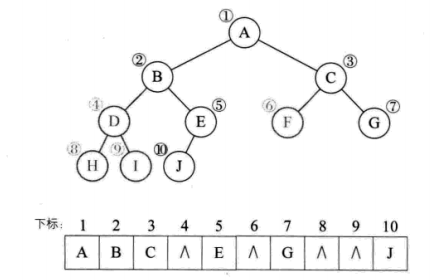
顺序存储结构一般只用于完全二叉树。

 

 

二叉链表

二叉树每个结点最多有两个孩子，所以为它设计一个数据域和两个指针域，我们称这样的链表叫做二叉链表。

 

结点结构图及代码如下：

 

结构示意图：

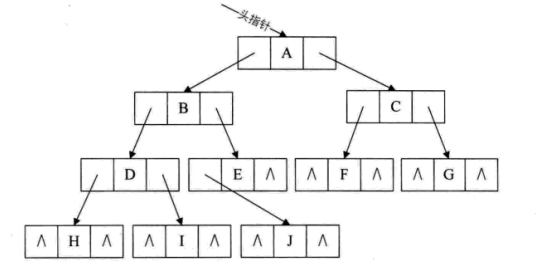
如果需要还可以增加一个指向其双亲的指针域，那样就称之为三叉链表。

 

 

遍历二叉树

二叉树遍历原理

 

二叉树遍历方法

1. 前序遍历

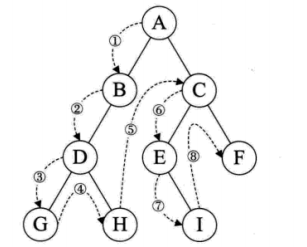
规则是若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

下图遍历的顺序为：ABDGHCEIF 

 

2. 中序遍历

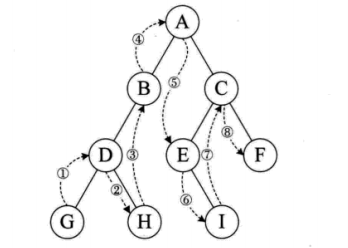
规则是若树为空，则空操作返回，否则从根结点开始（注意并不是先访问根结点），中序遍历根结点的左子树，然后是访问根结点，最后是中序遍历右子树。

下图的遍历顺序为：GDHBAEICF

 

3. 后序遍历

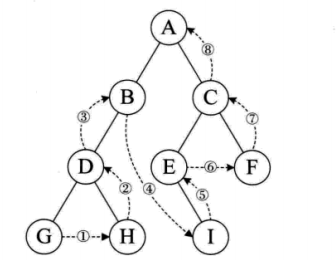
规则是若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左右子树，最后是访问根结点。

下图遍历的顺序为：GHDBIEFCA

 

4. 层序遍历

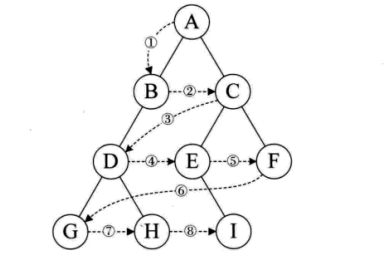
规则是若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中按从左到右的顺序对结点逐个访问。

下图的遍历顺序为：ABCDEFGHI

 

上面的四种遍历方法，其实都是把树中的结点变成某种意义的线性序列。

 

前序遍历算法

递归

 

中序遍历算法

 

后序遍历算法

 

推导遍历结果

已知前序遍历序列和中序遍历序列，可以唯一确定一棵二叉树。

已知后序便利序列和中序遍历序列，可以唯一确定一棵二叉树。

 

已知前序遍历序列和后序遍历序列是不能唯一确定一棵二叉树的。

 

 

二叉树的建立

建立二叉树，用到了递归的原理。

 

线索二叉树

线索二叉树原理

把指向前驱和后继的指针称为线索，加上线索的二叉链表称为线索链表，相应的二叉树称为线索二叉树（Threaded Binary Tree）

 

 

 

 

 

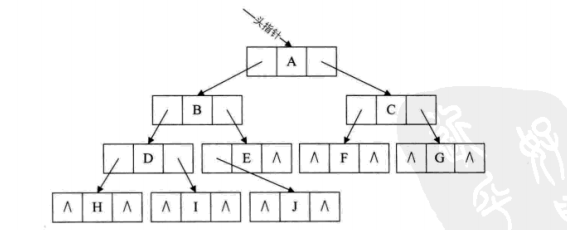
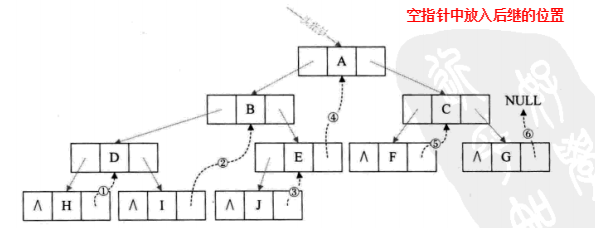
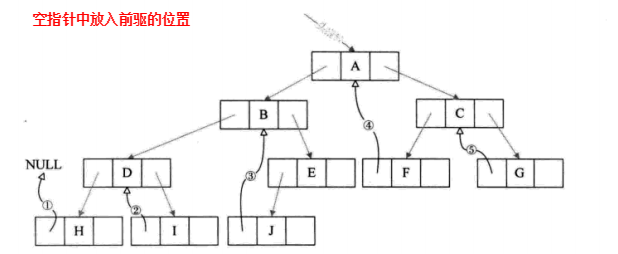
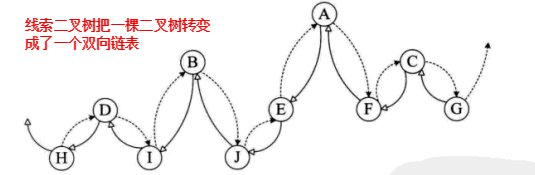
对二叉树以某种次序遍历使其变为线索二叉树的过程称作是线索化。

 

结点的结构如下所示：

 

 

 

线索二叉树结构实现

 线索化的实质就是将二叉链表中的空指针改为指向前驱或后继的线索。线索化的过程就是在遍历的过程中修改空指针的过程。

 

 

 

 

树、森林与二叉树的转换

 树转换为二叉树

 

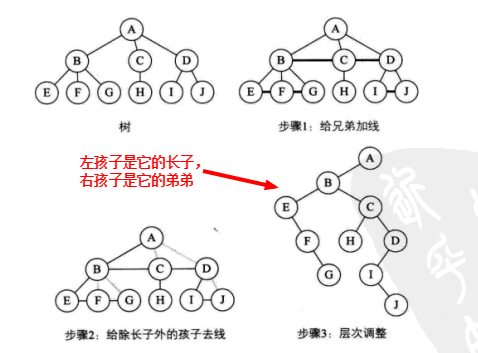
森林转换为二叉树

森林是由若干棵树组成的。

可以理解为，森林中的每一棵树都是兄弟，可以按照兄弟的处理方法来操作。

 

步骤如下：

 

 

 

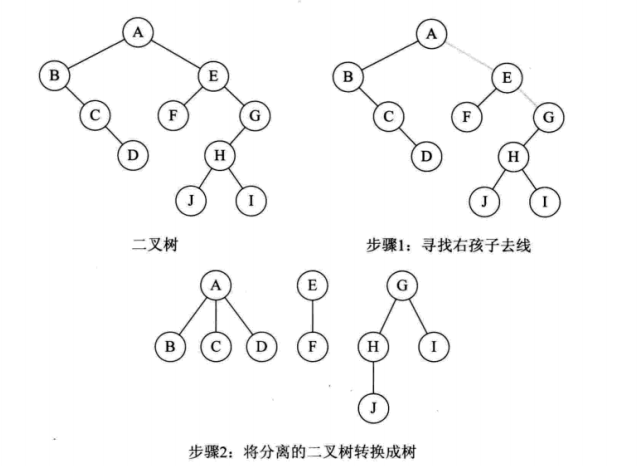
二叉树转换为树

 

 

 

二叉树转换为森林

判断一棵二叉树能转换成一棵树还是森林，就只要看这课二叉树的根结点有没有右孩子，有就是森林，没有就是一棵树。

 

 

树与森林的遍历

树的遍历有两种方式：

1. 先根遍历树，即先访问树的根结点，然后依次先根遍历根的每棵子树。

2. 后根遍历，即先依次后根遍历每棵子树，然后再访问根结点。

 

森林的遍历也有两种方式（同树）：

1. 前序遍历       2. 后序遍历

 

当以二叉链表做树的存储结构时，树的先根遍历和后根遍历完全可以借用二叉树的前序遍历和中序遍历的算法来实现。