第七章 图
图的存储结构
图不能用简单的顺序存储结构来表示。
而多重链表的方式,即以一个数据域和多个指针域组成的结点表示图中的一个顶点,尽管可以实现图结构,但是会有问题,比如若各个顶点的度数相差很大,按度数最大的顶点设计结点结构会造成很多存储单元的浪费,而若按每个顶点自己的度数设计不同的顶点结构,又带来操作的不便。
对于图来说,如何对它实现物理存储是个难题。图有以下五种不同的存储结构。
邻接矩阵
图的邻接矩阵(Adjacency Matrix)存储方式使用过两个数组来表示图。一个一维数组存储图中顶点信息,一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。


网中的权重也保存在二维数组中。

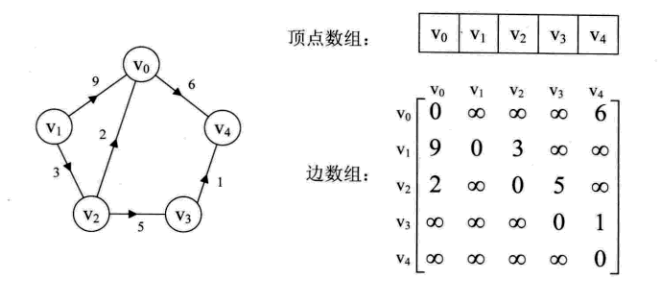
图的邻接矩阵存储结构的代码如下:

有了这个结构定义,我们构造一个图其实就是给顶点表和边表输入数据的过程。
n 个顶点和 e 条边的无向网图的创建,时间复杂度为O(n2+n+e).
缺点:
对于边数相对顶点较少的图,这种结构是存在对存储空间的极大浪费。

邻接表
邻接表:数组与链表相结合的存储方法称为邻接表(Adjacency List).

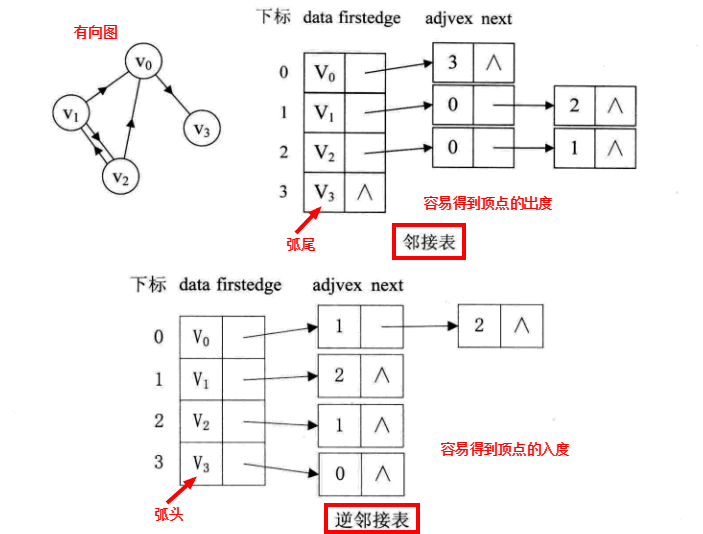

邻接表存储结构的代码如下:

对于邻接表的创建,时间复杂度为O(n + e).
十字链表(Orthogonal List)-- 有向图的优化存储
重新定义顶点表结点结构如下:

firstin表示入边表头指针,指向该顶点的入边表中第一个结点;firstout表示出边表头指针,指向该顶点的出边表中的第一个结点。
重新定义边表结点结构如下:

tailvex是指弧起点在顶点表的下标;headvex是指弧终点在顶点表中的下标;headlink是指入边表指针域,指向终点相同的下一条边;taillink是指出边表指针域,指向起点相同的下一条边。
如果是网,还可以再增加一个weight域来存储权值。

有向图的好处是把邻接表和逆邻接表整合在了一起,是有向图的非常好的数据类型。
邻接多重表 -- 无向图的优化存储
如果在无向图的应用中,关注的重点是顶点,那么邻接表是不错的选择,但如果关注的是边的操作,那么邻接表就比较麻烦了,需要优化。
重新定义的边表结点结构如下:

其中 ivex 和 jvex 是与某条边依附的两个顶点在顶点表中的下标。
ilink 指向依附顶点 ivex 的下一条边, jlink指向依附顶点 jvex的下一条边。
这就是邻接多重表结构。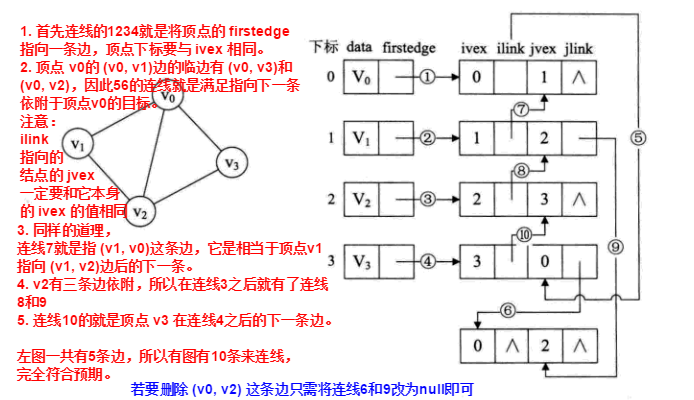

边集数组
边集数组是由两个一维数组构成。一个是存储顶点的信息;另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标、终点下标和权组成,如下图:

边数组结构的定义如下:
