载请注明出处:優YoU http://blog.csdn.net/lyy289065406/article/details/6727035
大致题意:
墙上有一面黑板,现划分为多个矩形,每个矩形都要涂上一种预设颜色C。
由于涂色时,颜料会向下流,为了避免处于下方的矩形的颜色与上方流下来的颜料发生混合,要求在对矩形i着色时,处于矩形i上方直接相邻位置的全部矩形都必须已填涂颜色。
在填涂颜色a时,若预设颜色为a的矩形均已着色,或暂时不符合着色要求,则更换新刷子,填涂颜色b。
注意:
1、 当对矩形i涂色后,发现矩形i下方的矩形j的预设颜色与矩形i一致,且矩形j上方的全部矩形均已涂色,那么j符合填涂条件,可以用 填涂i的刷子对j填涂,而不必更换新刷子。
2、 若颜色a在之前填涂过,后来填涂了颜色b,现在要重新填涂颜色a,还是要启用新刷子,不能使用之前用于填涂颜色a的刷子。
3、 若颜色a在刚才填涂过,现在要继续填涂颜色a,则无需更换新刷子。
4、 矩形着色不能只着色一部分,当确认对矩形i着色后,矩形i的整个区域将被着色。
首先要注意输入数据,每个矩形信息的输入顺序是 y x y x c,而不是 x y x y c
若弄反了x y坐标怎样也不会AC的.....
拓扑思想+DFS
方法还是很直观的,把每个矩形看作一个点,处于黑板最上方的矩形i入度为0,然后从矩形i出发,与其下方直接相邻的矩形连线,这些矩形的入度+1。换而言之,矩形a上方直接相邻的矩形数upNum,就是矩形a(点a)的入度数upNum。
当矩形i被涂色后,矩形i下方直接相邻的所有矩形的入度数-1。
那么若一个矩形的入度数为0时,它就是待涂色状态;入度不为0则不允许涂色。
然后就是按照题目要求的涂色限制条件,DFS涂色方案了,数据量较少,无需剪枝也能AC。
最后说说怎样判定矩形a在矩形b的上方。
矩形a与矩形b的基本位置关系共有3种,如下图:
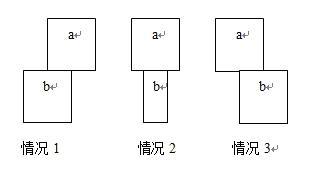
设矩形左上角的坐标为(Lx,Ly) 右下角的坐标为(Rx,Ry)
则先判断Rect[a].Ry==Rect[b].Ly,确定矩形a的底部和矩形b的顶部是否可能重合(直接相邻)
然后再判断3种情况:
情况1:
Rect[a].Lx>=Rect[b].Lx && Rect[a].Lx<Rect[b].Rx
情况2:
Rect[a].Lx<=Rect[b].Lx && Rect[a].Rx>=Rect[b].Rx
情况3:
Rect[a].Rx>Rect[b].Lx && Rect[a].Rx<=Rect[b].Rx
注意必须左右方向都要限制,其他特殊情况已由这3种关系所囊括。
Source修正:
Tehran 1999
http://code.google.com/p/djudge-core/downloads/detail?name=Tehran-1999.7z&can=2&q=
1 //Memory Time
2 //260K 0MS
3
4 #include<iostream>
5 using namespace std;
6
7 struct rectangle
8 {
9 int Lx,Ly; //左上角坐标
10 int Rx,Ry; //右下角坐标
11 int SetColor; //预设着色
12 bool flag; //标记当前矩形是否已着色
13 int UpNum; //该矩形上方的矩形数 (UpNum=0表示该矩形上方的矩形已全部被着色,该矩形为待着色状态)
14 int low[16]; //指向该矩形下方的矩形
15 int pl; //low[]指针
16 };
17
18 class info
19 {
20 public:
21 info(int n=0):N(n)
22 {
23 memset(color,false,sizeof(color));
24 Rect=new rectangle[N+1];
25 initial();
26
27 MinBrushNum=20; //最多只有15个矩形
28 DFS(0,0,1); //c==0表示当下对填涂的颜色暂无要求
29 }
30 ~info()
31 {
32 cout<<MinBrushNum<<endl;
33 delete[] Rect;
34 }
35 void initial(void);
36 bool Judge_Upper(int a,int b); //判断矩形a是否在矩形b上方
37 void DFS(int n,int c,int b); //n:当前已着色的矩形数,c:当前着色, b:当前正在用第b把刷子
38
39 protected:
40 int N; //矩形数量
41 rectangle* Rect; //N个矩形的信息
42 bool color[21]; //标记出现过的颜色
43 int MinBrushNum; //最少刷子数
44 };
45
46 void info::initial(void)
47 {
48 for(int k=1;k<=N;k++)
49 {
50 cin>>Rect[k].Ly>>Rect[k].Lx;
51 cin>>Rect[k].Ry>>Rect[k].Rx;
52 cin>>Rect[k].SetColor;
53
54 Rect[k].flag=false;
55 Rect[k].UpNum=0;
56 Rect[k].pl=0;
57
58 color[ Rect[k].SetColor ]=true;
59 }
60 for(int i=1;i<N;i++)
61 for(int j=i+1;j<=N;j++)
62 {
63 if(!Judge_Upper(i,j)) //若矩形i不在矩形j上方
64 Judge_Upper(j,i); //则判断矩形j是否在矩形i上方
65 }
66 return;
67 }
68
69 bool info::Judge_Upper(int a,int b)
70 {
71 if(Rect[a].Ry==Rect[b].Ly)
72 {
73 if((Rect[a].Lx>=Rect[b].Lx && Rect[a].Lx<Rect[b].Rx) || //情况1
74 (Rect[a].Lx<=Rect[b].Lx && Rect[a].Rx>=Rect[b].Rx) || //情况2
75 (Rect[a].Rx>Rect[b].Lx && Rect[a].Rx<=Rect[b].Rx)) //情况3
76 {
77 Rect[b].UpNum++;
78 Rect[a].low[ Rect[a].pl++ ]=b;
79 return true;
80 }
81 }
82 return false;
83 }
84
85 void info::DFS(int n,int c,int b)
86 {
87 if(n==N)
88 {
89 if(MinBrushNum > b)
90 MinBrushNum = b;
91 return;
92 }
93
94 if(c==0) //填涂颜色为随意时,枚举上方矩形均已被涂色的未涂色矩形
95 {
96 for(int i=1;i<=N;i++)
97 {
98 if(!Rect[i].flag && Rect[i].UpNum==0)
99 {
100 int j;
101
102 Rect[i].flag=true;
103 for(j=0;j<Rect[i].pl;j++) //第i个矩形下方的矩形的UpNum均-1
104 Rect[ Rect[i].low[j] ].UpNum--;
105
106 DFS(n+1,Rect[i].SetColor,b); //下一次填涂的颜色与当次一样,则用同一把刷子
107
108 Rect[i].flag=false;
109 for(j=0;j<Rect[i].pl;j++)
110 Rect[ Rect[i].low[j] ].UpNum++;
111 }
112 }
113 }
114 else //填涂颜色为上次填涂的颜色
115 {
116 bool tag=false;
117 for(int i=1;i<=N;i++)
118 {
119 if(Rect[i].SetColor==c && !Rect[i].flag && Rect[i].UpNum==0)
120 {
121 int j;
122 tag=true;
123
124 Rect[i].flag=true;
125 for(j=0;j<Rect[i].pl;j++) //第i个矩形下方的矩形的UpNum均-1
126 Rect[ Rect[i].low[j] ].UpNum--;
127
128 DFS(n+1,c,b); //下一次填涂的颜色与当次一样,则用同一把刷子
129
130 Rect[i].flag=false;
131 for(j=0;j<Rect[i].pl;j++)
132 Rect[ Rect[i].low[j] ].UpNum++;
133 }
134 }
135
136 if(!tag)
137 DFS(n,0,b+1); //颜色为c的矩形均已补满足填涂条件,启用新刷子填涂其他颜色
138 }
139 return;
140 }
141
142 int main(void)
143 {
144 int Case;
145 cin>>Case;
146 for(int c=1;c<=Case;c++)
147 {
148 int N;
149 cin>>N;
150 info POJ1691(N);
151 }
152 return 0;
153 }
Sample Input
8
7
0 0 2 2 1
0 2 1 6 2
2 0 4 2 1
1 2 4 4 2
1 4 3 6 1
4 0 6 4 1
3 4 6 6 2
14
0 0 3 2 3
0 2 2 4 1
0 4 1 8 4
1 4 2 7 2
1 7 3 8 1
2 2 3 7 4
3 4 7 6 3
3 6 7 8 4
5 0 8 3 3
5 3 6 4 2
8 0 9 3 2
6 3 9 4 1
7 4 9 8 2
3 0 5 4 4
4
0 0 3 1 1
0 1 2 5 2
0 5 3 6 1
2 1 3 5 1
13
0 0 3 3 1
0 3 2 4 2
0 4 2 5 1
2 3 5 4 1
2 4 3 5 3
3 4 6 5 2
3 2 4 3 1
3 0 4 2 2
4 0 8 1 3
4 1 5 3 2
5 1 6 4 3
6 1 8 3 1
6 3 8 5 1
13
0 0 3 3 1
0 3 2 4 2
0 4 2 5 1
2 3 5 4 1
2 4 3 5 2
3 4 6 5 2
3 2 4 3 1
3 0 4 2 2
4 0 8 1 3
4 1 5 3 2
5 1 6 4 3
6 1 8 3 1
6 3 8 5 1
6
0 0 2 3 9
2 0 3 3 1
3 0 4 3 9
4 0 5 3 1
5 0 6 3 9
6 0 7 3 1
8
0 0 2 3 9
0 3 2 5 1
2 0 3 2 1
2 2 3 4 1
2 4 3 5 2
3 0 4 3 1
3 3 4 5 2
4 0 5 5 3
12
0 0 8 3 9
0 3 2 9 1
2 3 4 5 1
2 5 4 8 1
2 8 4 9 1
4 3 6 4 2
4 4 6 7 2
4 7 5 9 1
5 7 7 9 1
6 3 8 5 1
6 5 8 7 1
7 7 8 9 1
Sample Output
3
8
2
6
5
6
4
4