[LeetCode 1274] Number of Ships in a Rectangle

(This problem is an interactive problem.)

On the sea represented by a cartesian plane, each ship is located at an integer point, and each integer point may contain at most 1 ship.

You have a function Sea.hasShips(topRight, bottomLeft) which takes two points as arguments and returns true if and only if there is at least one ship in the rectangle represented by the two points, including on the boundary.

Given two points, which are the top right and bottom left corners of a rectangle, return the number of ships present in that rectangle.  It is guaranteed that there are at most 10 ships in that rectangle.

Submissions making more than 400 calls to hasShips will be judged Wrong Answer.  Also, any solutions that attempt to circumvent the judge will result in disqualification.

 

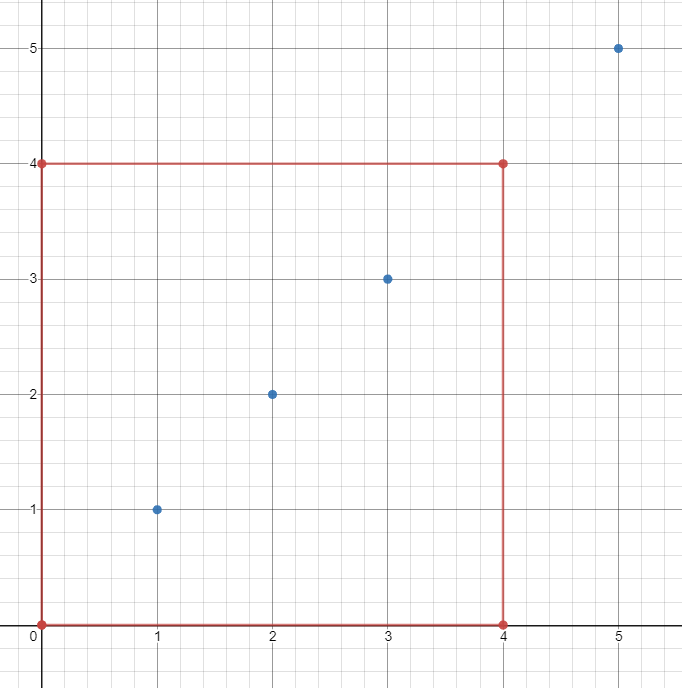
Example :

Input: 
ships = [[1,1],[2,2],[3,3],[5,5]], topRight = [4,4], bottomLeft = [0,0]
Output: 3
Explanation: From [0,0] to [4,4] we can count 3 ships within the range.

 

Constraints:

• On the input ships is only given to initialize the map internally. You must solve this problem "blindfolded". In other words, you must find the answer using the given hasShips API, without knowing the ships position.
• 0 <= bottomLeft[0] <= topRight[0] <= 1000
• 0 <= bottomLeft[1] <= topRight[1] <= 1000

Apply divide and conquer here. Divide the current searching region into 4 equal smaller regions. Do this recursively with the following base case:

1. if the current search region is not valid or it has no ships in it, return 0;

2. if the current search region is a single point, return 1.

 

Runtime: T(N) = 4*T(N/4) + O(N^0); a = 4 > b^d = 4^0 = 1; case 3 of the master method, T(N) = O(N^(loga / logb)) = O(N).

One implementation pitfall is that since you compute the middle point using: bottomLeft + (topRight - bottomLeft) / 2, when bottomLeft and topRight are off by 1, the middle point will be bottomLeft. To avoid non-ending recursion bug, recurse on (bottomLeft, middle point) and (middle point + 1, topRight). For example, if bottomLeft is (1, 1) and topRight is (2, 2), middle point will be (1, 1). Recurse on (bottomLeft, middle point) and (middle point + 1, topRight) leads to 2 base case(single point(1, 1) and (2,2)); However, recurse on (bottomLeft, middle point + 1) and (middle point, topRight) leads to recursing on the same region(1,1) and (2,2) again, causing stackoverflow.

 

Proof that this algorithm makes at most 400 hasShips calls. 

For simplicity, let's assume the upper bound is 1024 * 1024 instead of 1000 * 1000, if we can prove for 1024 * 1024 then certainly the 1000 * 1000 case meets this condition. 

At the top level, we make 4 hasShip calls. The next level we make at most 4 * 4 = 16 calls. Each search region has been reduced to 256 * 256. Starting from this level, since we know that there are at most 10 ships in total, we will recurse on at most 10 search regions, each recursion on each region makes 4 calls. So that is at most 10 * 4 calls each level down, until we reach the base case. 256 == 2^8, to reach the base case, 

2's power goes from 8 to 0, decreasing by 1 each level down. 8 * 40 + 4 + 16 = 340 < 400.

Q.E.D

/**
 * // This is Sea's API interface.
 * // You should not implement it, or speculate about its implementation
 * class Sea {
 *     public boolean hasShips(int[] topRight, int[] bottomLeft);
 * }
 */

class Solution {
    public int countShips(Sea sea, int[] topRight, int[] bottomLeft) {
        return divideAndConquer(sea, topRight, bottomLeft);
    }
    private int divideAndConquer(Sea sea, int[] topRight, int[] bottomLeft) {
        if(topRight[0] < bottomLeft[0] || topRight[1] < bottomLeft[1] || !sea.hasShips(topRight, bottomLeft)) {
            return 0;
        }
        if(topRight[0] == bottomLeft[0] && topRight[1] == bottomLeft[1]) {
            return 1;
        }
        int cnt = 0;
        int midX = bottomLeft[0] + (topRight[0] - bottomLeft[0]) / 2;
        int midY = bottomLeft[1] + (topRight[1] - bottomLeft[1]) / 2;
                
        cnt += divideAndConquer(sea, new int[]{midX, midY}, bottomLeft);
        cnt += divideAndConquer(sea, new int[]{topRight[0], midY}, new int[]{midX + 1, bottomLeft[1]});
        cnt += divideAndConquer(sea, new int[]{midX, topRight[1]}, new int[]{bottomLeft[0], midY + 1});
        cnt += divideAndConquer(sea, topRight, new int[]{midX + 1, midY + 1});
        return cnt;
    }
}