[LeetCode 1530] Number of Good Leaf Nodes Pairs

Given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Return the number of good leaf node pairs in the tree.

 

Example 1:

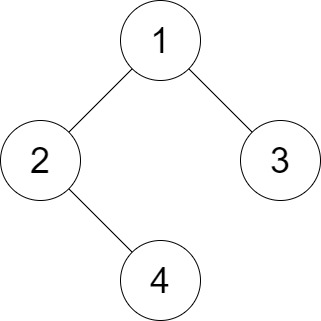
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2:

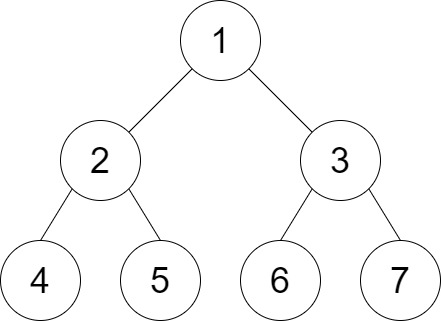
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

Example 3:

Input: root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
Output: 1
Explanation: The only good pair is [2,5].

Example 4:

Input: root = [100], distance = 1
Output: 0

Example 5:

Input: root = [1,1,1], distance = 2
Output: 1

 

Constraints:

• The number of nodes in the tree is in the range [1, 2^10].
• Each node's value is between [1, 100].
• 1 <= distance <= 10

Solution that you came up during contest

Since we have up to 1024 nodes, a O(N^2) solution is efficient to get accepted. The algorithm is very straightforward. 

1.   Different tree nodes may share the same value, so for easier implemenation, do a dfs or bfs to relabel all N nodes from 0 to N - 1.

2.  Convert the given binary tree to an undirected graph, either by dfs or bfs. Save all the leaf tree nodes during this conversion. 

3.  For each leaf node, do a bfs on the converted graph, adding all other leaf nodes within specified distance. Terminate bfs if all nodes are exhausted or the current distance exceeds specified max distance.

4.  Divide the total count from step 3 as we counted each pair twice.

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    private int currLabel = 0;
    private boolean[] leafNodes;
    public int countPairs(TreeNode root, int distance) {
        dfsRelabel(root);
        leafNodes = new boolean[currLabel];
        List<Integer>[] g = buildGraph(root);
        int ans = 0;
        for(int i = 0; i < leafNodes.length; i++) {
            if(leafNodes[i]) {
                ans += bfs(g, i, distance);
            }            
        }
        return ans / 2;
    }
    private int bfs(List<Integer>[] g, int node, int distance) {
        Queue<Integer> q = new LinkedList<>();
        boolean[] visited = new boolean[g.length];
        
        q.add(node);
        visited[node] = true;
        int d = 0, cnt = 0;
        
        while(q.size() > 0 && d <= distance) {
            int sz = q.size();
            for(int i = 0; i < sz; i++) {
                int curr = q.poll();
                if(curr != node && d <= distance && leafNodes[curr]) {
                    cnt++;
                }
                for(int u : g[curr]) {
                    if(!visited[u]) {
                        visited[u] = true;
                        q.add(u);
                    }
                }
            }
            d++;
        }
        return cnt;
    }
    private void dfsRelabel(TreeNode node) {
        if(node != null) {
            dfsRelabel(node.left);
            dfsRelabel(node.right);
            node.val = currLabel;
            currLabel++;
        }
    }
    private void buildGraphHelper(List<Integer>[] g, TreeNode node) {
        if(node != null) {
            buildGraphHelper(g, node.left);
            buildGraphHelper(g, node.right);
            if(node.left != null) {
                g[node.val].add(node.left.val);
                g[node.left.val].add(node.val);
            }
            if(node.right != null) {
                g[node.val].add(node.right.val);
                g[node.right.val].add(node.val);
            }
            if(node.left == null && node.right == null) {
                leafNodes[node.val] = true;
            }
        }
    }
    private List<Integer>[] buildGraph(TreeNode root) {
        List<Integer>[] g = new List[currLabel];
        for(int i = 0; i < g.length; i++) {
            g[i] = new ArrayList<>();
        }
        buildGraphHelper(g, root);
        return g;
    }
    
}

A better O(N) DFS solution

For any good pair(u, v), there is only one subtree T such that u is in T's left-subtree and v is in T's right-subtree.(Or u in T's right-subtree, v in T's left-subtree). This means we can do a dfs on the entire tree and for each node(a different node represents the root of a different subtree), compute the following 2 results.

1. LD[i]: where LD[i] is the number of leaf nodes that are of distance i to the left-subtree's root node;

2.RD[i]: where RD[i] is the number of leaf nodes that are of distance i to the right-subtree's root node;

Base case: 

1. if node is null, return an array of 0.

2. if node is a leafnode, set d[0] = 1, representing that there is 1 leaf node that is of distance 0 to the leaf node itself.

General case:

After getting LD and R, we enumerate all possible left and right leaf node distance combination and update final answer accordingly. We then update the current node's computing result using d[i + 1] = ld[i] + rd[i]; This means the number of leaf nodes that are of distance i + 1 to the current node is the sum of the leaf nodes of distance i from the left and right subtree. 

Because we visit each node only once and distance is at most 10, the overall runtime is O(N).

class Solution {
    private int ans = 0;
    public int countPairs(TreeNode root, int distance) {
        dfs(root, distance);
        return ans;
    }
    private int[] dfs(TreeNode node, int distance) {
        int[] d = new int[distance];
        if(node == null) {
            return d;
        }
        if(node.left == null && node.right == null) {
            d[0] = 1;
            return d;
        }
        int[] ld = dfs(node.left, distance);
        int[] rd = dfs(node.right, distance);
        for(int i = 0; i < ld.length; i++) {
            for(int j = 0; j < rd.length; j++) {
                if(i + 1 + j + 1 <= distance) {
                    ans += ld[i] * rd[j];
                }
            }
        }
        for(int i = 0; i < d.length - 1; i++) {
            d[i + 1] = ld[i] + rd[i];
        }
        return d;
    }
}