In universe Earth C-137, Rick discovered a special form of magnetic force between two balls if they are put in his new invented basket. Rick has n empty baskets, the ith basket is at position[i], Morty has m balls and needs to distribute the balls into the baskets such that the minimum magnetic force between any two balls is maximum.
Rick stated that magnetic force between two different balls at positions x and y is |x - y|.
Given the integer array position and the integer m. Return the required force.
Example 1:
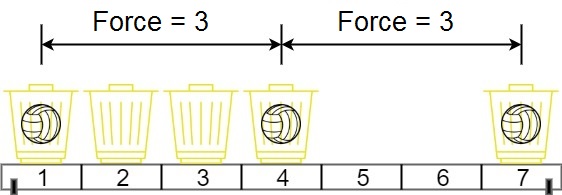
Input: position = [1,2,3,4,7], m = 3
Output: 3
Explanation: Distributing the 3 balls into baskets 1, 4 and 7 will make the magnetic force between ball pairs [3, 3, 6]. The minimum magnetic force is 3. We cannot achieve a larger minimum magnetic force than 3.
Example 2:
Input: position = [5,4,3,2,1,1000000000], m = 2
Output: 999999999
Explanation: We can use baskets 1 and 1000000000.
Constraints:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- All integers in
positionare distinct. 2 <= m <= position.length
Incorrect algorithm you came up during contest: when m is 2, we pick the 1st and last positions. If m is 3, then we would pick the position that is the closest to the middle value of the 1st position and last position. This will then divide remaining unpicked positions into 2 segments. Generalizing this idea, each time we need to place one more ball, we pick the segment that provides the maximum min force. This can be done by using priority queue and binary search: keep a max pq for all segments that have their index range, next pick index and the maximum min force they offer. After processing a segment, we generate 2 possible smaller disjoint segments and apply binary search to get the next pick index. (Solving this problem: given a sorted array and a target, find the index such that the value at that index is the closest to target in O(logN) time).
Although this is a good practice solving another problem, the above algorithm is incorrect. The case of m = 3 does not generalize for bigger m. Consider this counter example:
positions = {1,2,3,4,5,6,7,8,9,10}, m = 4; using the above algorithm, we'd pick 1, 5, 7, 10 and the answer is 2. But if we pick 1, 4, 7, 10, the answer will be 3!
class Solution { public int maxDistance(int[] p, int m) { Arrays.sort(p); int n = p.length; int ans = p[n - 1] - p[0]; m -= 2; PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> { return b[3] - a[3]; }); int idx = closestToTarget(p, 1, n - 2, p[0] + (p[n - 1] - p[0]) / 2); pq.add(new int[]{1, n - 2, idx, Math.min(p[n - 1] - p[idx], p[idx] - p[0])}); while(m > 0) { int[] e = pq.poll(); ans = Math.min(ans, e[3]); int l1 = e[0], r1 = e[2] - 1, l2 = e[2] + 1, r2 = e[1]; if(l1 <= r1) { int idx1 = closestToTarget(p, l1, r1, p[l1] + (p[r1] - p[l1]) / 2); pq.add(new int[]{l1, r1, idx1, Math.min(p[r1 + 1] - p[idx1], p[idx1] - p[l1 - 1])}); } if(l2 <= r2) { int idx2 = closestToTarget(p, l2, r2, p[l2] + (p[r2] - p[l2]) / 2); pq.add(new int[]{l2, r2, idx2, Math.min(p[r2 + 1] - p[idx2], p[idx2] - p[l2 - 1])}); } m--; } return ans; } // binary search to find the index such that p[index] is the closeset to the target value private int closestToTarget(int[] p, int start, int end, int target) { int l = start, r = end; while(l < r - 1) { int mid = l + (r - l) / 2; if(p[mid] <= target) { l = mid; } else { r = mid; } } if(Math.abs(p[l] - target) <= Math.abs(p[r] - target)) { return l; } return r; } }
The RIGHT binary search
we should do binary search on the final answer as it must be in the range of [1, max position - min position]. This is O(10^9). Given a min force D, it takes O(N) time to check we can meet this condition. Place a ball as soon as we have a position that has a minimum gap of D than the previously placed position. This greedy approach works because if we can place the same at a later position and meet the min D condition, placing right now will only give us more gaps to manuver.
Why binary search on answer works in this problem?
Because for a given min force D, if we can not satisfy it, that means all answers > D can be excluded; If it can be satisfied, it means we can at least get an answer D, there might be a better answer but we have to keep searching on the right half without excluding D.
class Solution { public int maxDistance(int[] p, int m) { Arrays.sort(p); int n = p.length, l = 1, r = p[n - 1] - p[0]; while(l < r - 1) { int mid = l + (r - l) / 2; if(check(p, mid, m)) { l = mid; } else { r = mid - 1; } } if(check(p, r, m)) { return r; } return l; } // check if m items can be placed with minimum distance minD private boolean check(int[] p, int minD, int m) { int cnt = 1; int next = p[0] + minD; for(int i = 1; i < p.length; i++) { if(p[i] >= next) { cnt++; next = p[i] + minD; } } return cnt >= m; } }