[Coding Made Simple / LeetCode 1235] Maximum Profit in Job Scheduling

Given certain jobs with start and end time and amount you make on finishing the job, find the maximum value you can make by scheduling jobs in non-overlapping way.

Dynamic programming solution. O(N^2) runtime, O(N) space

First sort all the jobs in ascending order based on their end time. This makes checking if two jobs overlap or not easier. 

State: maxGain[i]: Given the first i jobs, the max profit we can get by selecting jobs[i]. 

Function: maxGain[i] = max {maxGain[i], maxGain[j] + jobs[i].gain}, for j in [0, i)

Initialization: maxGain[i] = jobs[i].gain, as we know by selecting jobs[i], we at least have a profit of jobs[i].gain.

Answer:  the max value of maxGain[i]. 

import java.util.Arrays;

class Job implements Comparable<Job>{
    int start;
    int end;
    int gain;
    Job(int start, int end, int gain) {
        this.start = start;
        this.end = end;
        this.gain = gain;
    }
    public int compareTo(Job o) {
        return this.end - o.end;
    }
}
public class WeightedJobScheduling {
    public int getMaxGain(Job[] jobs) {
        Arrays.sort(jobs);
        int[] maxGain = new int[jobs.length];
        for(int i = 0; i < maxGain.length; i++) {
            maxGain[i] = jobs[i].gain;
        }
        for(int i = 1; i < maxGain.length; i++) {
            for(int j = 0; j < i; j++) {
                if(jobs[i].start >= jobs[j].end) {
                    maxGain[i] = Math.max(maxGain[i], maxGain[j] + jobs[i].gain);
                }
            }
        }
        
        int max = Integer.MIN_VALUE;
        for(int i = 0; i < maxGain.length; i++) {
            if(maxGain[i] > max) {
                max = maxGain[i];
            }
        }
        return max;
    }
}

This is the same problem with https://leetcode.com/problems/maximum-profit-in-job-scheduling/

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

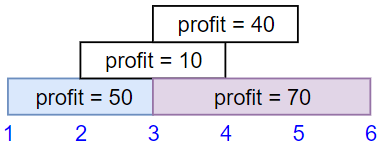
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

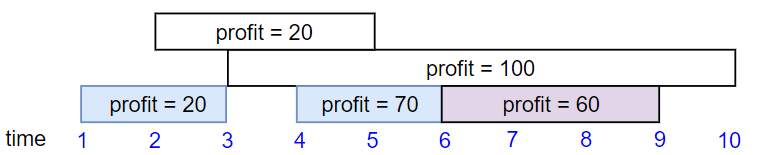
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
• 1 <= startTime[i] < endTime[i] <= 10^9
• 1 <= profit[i] <= 10^4

Given the input size of 5 * 10^4, the previous O(N^2) solution is too slow. The bottleneck is that the O(N^2) solution requires O(N) time to find the maximum job profit from 0 to i - 1 jobs that does not overlap with the ith job. Since we already sorted all the jobs based on their end time, we know that for two index j and k, if j < k, if the kth job does not overlap the ith job, the jth job does not overlap with the ith job either. If we can make sure that the biggest index of j < i gives us the max profit from scheduling 0 to jth jobs, we can apply binary search to speed up the runtime from O(N) to O(logN). 

We achieve the above goal by redefining dp[i] to be the max profit out of 0 to the ith jobs,  not the max profit out of 0 to the ith jobs with the ith job scheduled.  The dynamic programming state definition in the O(N^2) solution forces us to check each smaller index in order to find the max profit that does not overlap the ith job. 

state: dp[i]: max profit out of 0 to ith jobs
dp[i] = Math.max(dp[i - 1], max profit out of 0 to ith jobs, including the ith job)

O(N * log N) runtime

class Solution {
    class Job {
        int start, end, profit;
        Job(int start, int end, int profit) {
            this.start = start;
            this.end = end;
            this.profit = profit;
        }
        int getEnd() {
            return end;
        }
    }
    public int jobScheduling(int[] startTime, int[] endTime, int[] profit) {
        int n = profit.length;
        Job[] jobs = new Job[n];
        for(int i = 0; i < n; i++) {
            jobs[i] = new Job(startTime[i], endTime[i], profit[i]);
        }
        Arrays.sort(jobs, Comparator.comparingInt(Job::getEnd));
        
        //dp[i]: max profit out of 0 to ith jobs
        //dp[i] = Math.max(dp[i - 1], max profit out of 0 to ith jobs, including the ith job)
        int[] dp = new int[n];
        dp[0] = jobs[0].profit;
        
        for(int i = 1; i < n; i++) {
            int currProfit = jobs[i].profit;
            //find the max profit out of all 0 to i - 1 jobs that has no intersection with the current job.
            //A linear search causes TLE; since we already sorted jobs based on their end time and the dp
            //array is sorted in non-decreasing nature(always pick the max possible value). This means as long
            //as we find the largest j, j < i, that jobs[j].endTime <= jobs[i].startTime, we can just skip all
            //the rest jobs k with k < j, because dp[k] <= dp[j].
            int lastNonOverLapIdx = binarySearch(jobs, 0, i - 1, jobs[i].start);
            currProfit += lastNonOverLapIdx >= 0 ? dp[lastNonOverLapIdx] : 0;
            dp[i] = Math.max(currProfit, dp[i - 1]);
        }
        return dp[n - 1];
    }
    private int binarySearch(Job[] jobs, int l, int r, int t) {
        while(l < r - 1) {
            int mid = l + (r - l) / 2;
            if(jobs[mid].end <= t) {
                l = mid;
            }
            else {
                r = mid - 1;
            }
        }
        if(jobs[r].end <= t) {
            return r;
        }
        else if(jobs[l].end <= t) {
            return l;
        }
        return -1;
    }
}