关联规则挖掘的研究一直是数据挖掘领域的一个重要方向。
关联规则挖掘的目的是从大型事务数据库中挖掘出不同项目之间的关联关系 ,找出潜在的行为模式。
关联规则概念是由 Agrawal 等人在1993年率先提出的, 并随后提出了Apriori算法。
基本概念:
定义1 关联规则挖掘的事务数据库记为TDB,TDB={T1,T2,…,Tk},Tk={i1,i2,…,ip},Tk称为事务,ip称为项目。
定义2 设I={i1,i2,…,im}是TDB中全体项目组成的集合。每一个事务T是I中一组项目的集合,即 ![]() ,每个T有一个唯一的标识符TID。
,每个T有一个唯一的标识符TID。
定义3 设项目集X是I中项目的集合,如果X中有k个项目,那么称X的长度为k,记为k项目集。
定义4 如果项目集 ![]() ,则称事务T满足项目集X,项目集X在事务数据库TDB中的支持度,记为Support(X),即事务数据库TDB中满足项目集X的事务数占总事务数的比例。
,则称事务T满足项目集X,项目集X在事务数据库TDB中的支持度,记为Support(X),即事务数据库TDB中满足项目集X的事务数占总事务数的比例。
定义5 如果项目集X在事务数据库TDB中的支持度不小于用户或专家给定的最小支持度阈值,那么称项目集X为频繁项目集,反之称为非频繁项目集。
定义6 一条关联规则就是形如 ![]() 的蕴涵式,其中
的蕴涵式,其中![]() 。X称为规则的前件,Y称为规则的后件。
。X称为规则的前件,Y称为规则的后件。
定义7 同时满足最小置信度阈值和最小支持度阈值的关联规则为强关联规则。
关联规则挖掘可以分解为下列两个子问题:
(1)找出所有频繁项目集 ,这些项目集在 TDB 中的支持度不小于最小支持度 min_sup ;
(2)由频繁项目集产生强关联规则 ,这些规则必须满足最小置信度 min_conf 。
先看一个简单的例子,假如有下面数据集,每一组数据ti表示不同的顾客一次在商场购买的商品的集合:
t1: 牛肉、鸡肉、牛奶
t2: 牛肉、奶酪
t3: 奶酪、靴子
t4: 牛肉、鸡肉、奶酪
t5: 牛肉、鸡肉、衣服、奶酪、牛奶
t6: 鸡肉、衣服、牛奶
t7: 鸡肉、牛奶、衣服
假如有一条规则:牛肉—>鸡肉,那么同时购买牛肉和鸡肉的顾客比例是3/7,而购买牛肉的顾客当中也购买了鸡肉的顾客比例是3/4。这两个比例参数是很重要的衡量指标,它们在关联规则中称作支持度(support)和置信度(confidence)。对于规则:牛肉—>鸡肉,它的支持度为3/7,表示在所有顾客当中有3/7同时购买牛肉和鸡肉,其反应了同时购买牛肉和鸡肉的顾客在所有顾客当中的覆盖范围;它的置信度为3/4,表示在买了牛肉的顾客当中有3/4的人买了鸡肉,其反应了可预测的程度,即顾客买了牛肉的话有多大可能性买鸡肉。
对于支持度和置信度,我们需要正确地去看待这两个衡量指标。一条规则的支持度表示这条规则的可能性大小,如果一个规则的支持度很小,则表明它在事务集合中覆盖范围很小,很有可能是偶然发生的;如果置信度很低,则表明很难根据X推出Y。
其实可以从统计学和集合的角度去看这个问题, 假如看作是概率问题,则可以把“顾客买了牛肉之后又多大可能性买鸡肉”看作是条件概率事件,而从集合的角度去看,可以看下面这幅图:
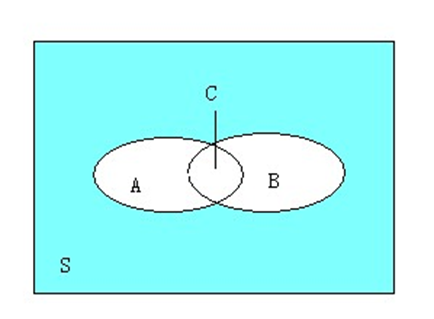
上面这副图可以很好地描述这个问题,S表示所有的顾客,而A表示买了牛肉的顾客,B表示买了鸡肉的顾客,C表示既买了牛肉又买了鸡肉的顾客。那么C.count/S.count=3/7,C.count/A.count=3/4。
上述例子中的所有商品集合I={牛肉,鸡肉,牛奶,奶酪,靴子,衣服}称作项目集合,每位顾客一次购买的商品集合ti称为一个事务,所有的事务T={t1,t2,....t7}称作事务集合,并且满足ti是I的真子集。
一条关联规则是形如下面的蕴含式:
X—>Y,X,Y满足:X,Y是I的真子集,并且X和Y的交集为空集。其中X称为前件,Y称为后件。
对于规则X—>Y,根据上面的例子可以知道它的支持度(support)=(X,Y).count/T.count,置信度(confidence)=(X,Y).count/X.count 。
其中(X,Y).count表示T中同时包含X和Y的事务的个数,X.count表示T中包含X的事务的个数。
关联规则挖掘则是从事务集合中挖掘出满足支持度和置信度最低阈值要求的所有关联规则,这样的关联规则也称强关联规则。

Apriori算法
这里的主要问题在于,寻找物品的不同组合是一项十分耗时的任务,所需的计算代价很高,蛮力搜索并不能解决这个问题。因此此处介绍使用Apriori算法来解决上述问题
主要算法流程:
1. 扫描数据库,生成候选1项集和频繁1项集。
2. 从2-项集开始循环,由频繁k-1项集生成频繁频繁k项集。
2.1 频繁k-1项集两两组合,判定是否可以连接,若能则连接生成k项集。(连接)
2.2 对k项集中的每个项集检测其子集是否频繁,舍弃掉子集不是频繁项集即:不在频繁k-1项集中的项集。(剪枝)
(先验性质:频繁项集的所有非空子集也一定是频繁的。)
2.3 扫描数据库,计算2.3步中过滤后的k项集的支持度,舍弃 掉支持度小于阈值的项集,生成频繁k项集。
3. 若当前k项集中只有一个项集时循环结束。
一个例子理解Apriori算法:
1.生成频繁项集
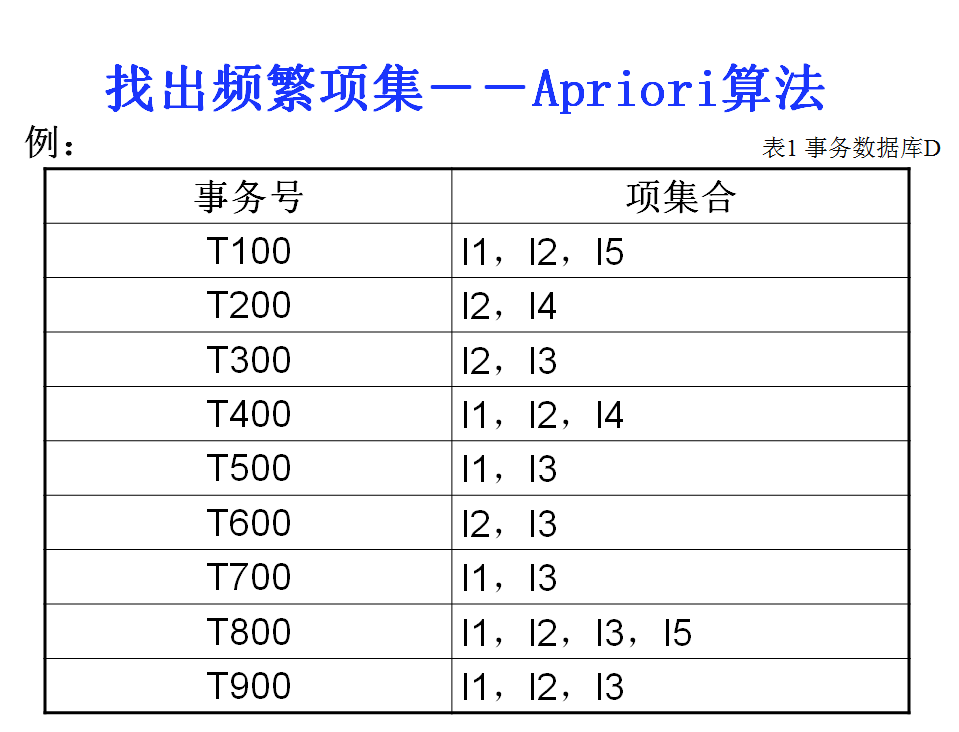
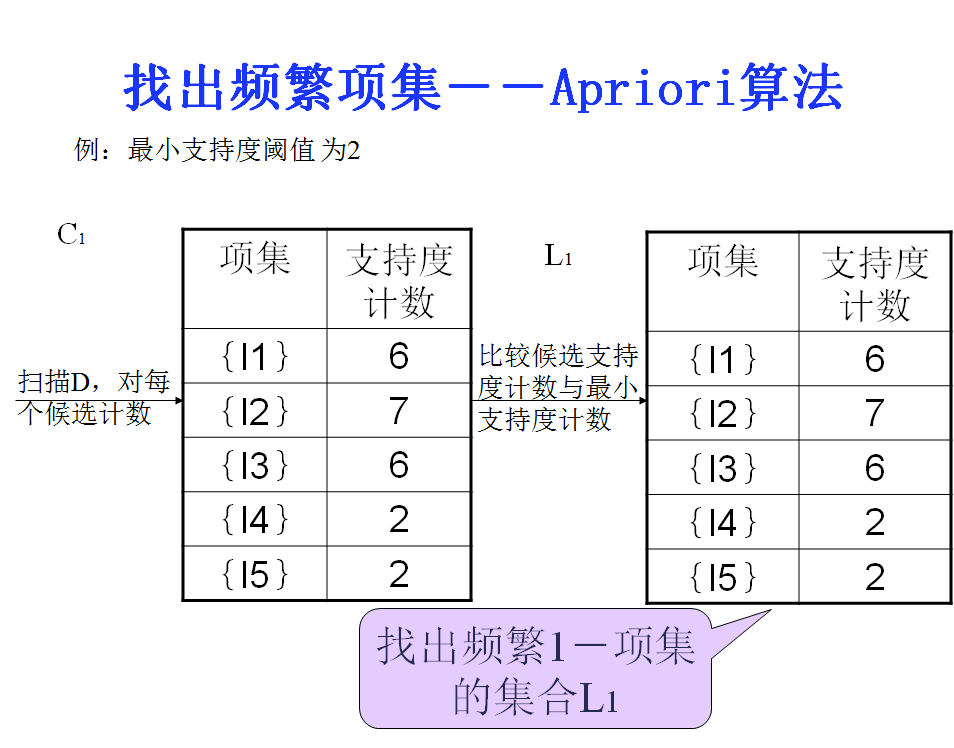
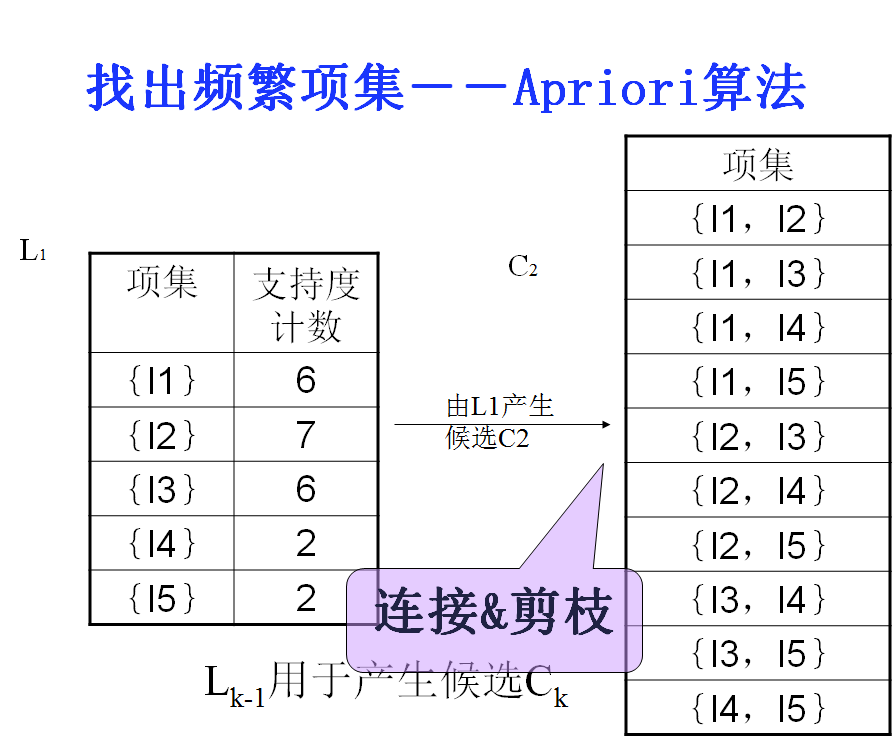
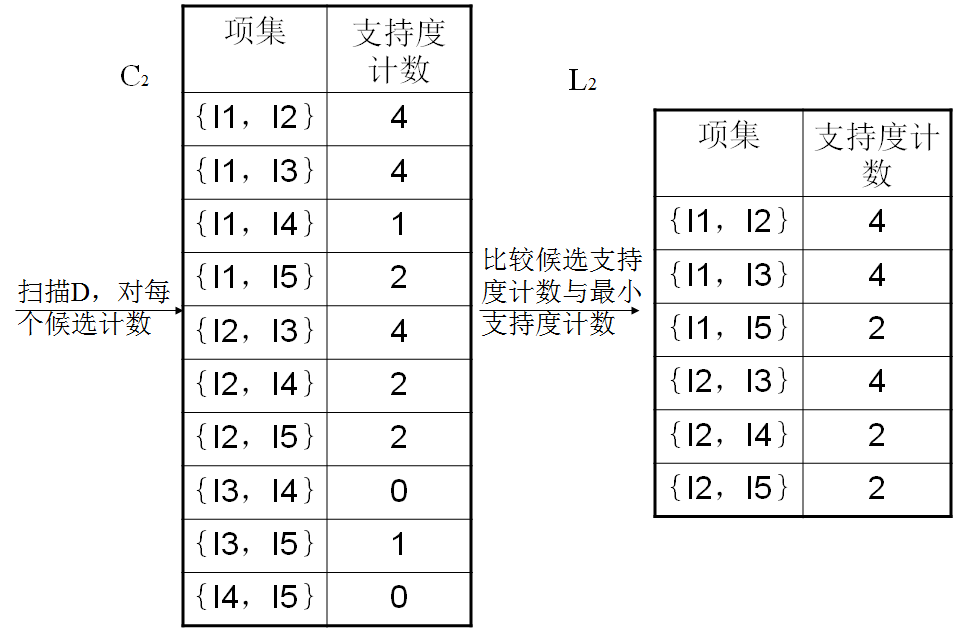



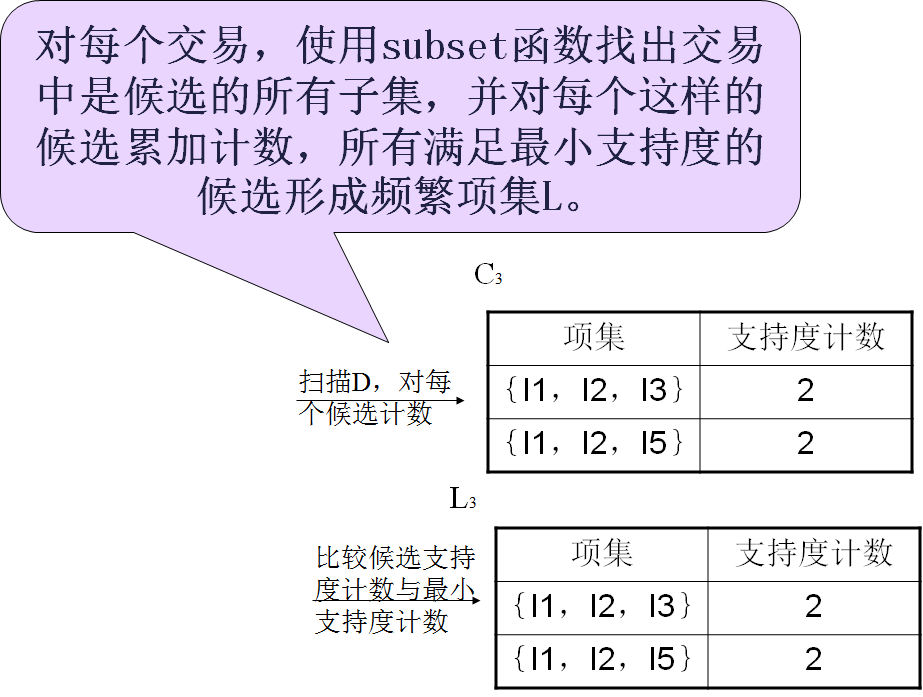
2.生成强关联规则
这里只说明3-频繁项目集生成关联规则的过程:
对于集合{I1,I2,I5}
先生成1-后件的关联规则:
(I1,I2)—>I5, 置信度=2/4=50% (I1,I5)—>I2, 置信度=2/2=100% (I2,I5)—>I1, 置信度=2/2=100%
再生成2-后件的关联规则:
I1—>(I2,I5) 置信度=2/6=33% I2—>(I1,I5) 置信度=2/7=29% I5—>(I1,I2) 置信度=2/2=100%
如果最小置信度阈值是70%,则对于3-频繁项目集生成的强关联规则为:(I1,I5)—>I2,(I2,I5)—>I1 和 I5—>(I1,I2)
Apriori 算法能够比较有效地产生频繁项目集 ,但也存在着以下缺点:
(1)数据库扫描的次数太多,每次寻找 k 频繁项目集( k =1 , …, n) 时都需要扫描数据库一次来获得候选项目集的支持度 ,共需要扫描 n 次。如果遇到海量数据库,或者 n 太大时,耗时太长, 难以满足实际应用 。
(2)算法效率不高, 利用 k 频繁项目集连接产生 k +1 候选项目集 ,判断连接条件时重复比较次数太多 。对于长度为 m,项目集个数为 n 的频繁项目集 Lm ,判断可连接条件时比较所耗的时间复杂度为O( m *n2)。